3.5.4: The Number e

Last updated
Save as PDF

Page ID: 14384

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

The Transcendental Number e and Natural Log

The Transcendental Number e

This section introduces the transcendental number e which is a special number that is considered a natural base. In addition to exploring how to simplify and solve equations with e, this section also investigates how it can be used to understand compounding interest and real life situations with exponential growth and decay.

Warm-Up

Compounding interest monthly, annually or over any other discrete interval can easily be modeled with exponential functions. Use the interactive below to explore an exponential model that compounds annually. Later in this section you will see how the number e can be used to model interest rates that are compounded continuously.

Interactive*

Investigation

Work it Out 1

Gianna opens a savings account with $1,000 and it accrues interest monthly at a rate of 5%. What is the balance in the account after the first month? After 2 months? After 1 year? After 2 years? Can you write an equation that would allow you to determine the account balance after m months?

Look at the process you've used to calculate the value after the second month. You started with $1,000 which is called the Principal, and multiplied it by 1.05 (which is the same as adding 5% of the value of the Principal back to the Principal). The second month you multiplied by 1.05 again, and will continue doing so for as many months as you're trying to calculate. This repeated multiplication suggests the equation will contain an exponent.

Discussion

After 1 month, her bank account will have the original $1,000 plus 5% interest ($50.00), or $1,050.00. After the second month she will have the monthly starting balance ($1,050.00) plus 5% of that ($52.50), or a total of $1,102.50. You can continue this process to calculate her balance after 1 or 2 years. Is there a shortcut? In other words, what equation would allow you to more quickly determine her balance?

Work it Out 2

Start with the equation: $\ \left(1+\frac{1}{n}\right)^{n}$.

Construct a table that shows what happens to the overall value of this expression as n gets larger. Round each decimal to the nearest 4 decimal places.
Based on your table, does it seem like the overall value is approaching a certain number? If so, what do you think this number is?
Estimate the value of the expression when n=100 and when n=1,000.
Explain how you made these estimates.
As n approaches infinity, what does the value of the expression approach?

Discussion

The start to a table is below. Fill in the missing values, and continue to add others.

n	$\ \left(1+\frac{1}{n}\right)^{n}$
1	$\ \left(1+\frac{1}{1}\right)^{1}=2$
2	$\ \left(1+\frac{1}{2}\right)^{2}=2.25$
3	$\ \left(1+\frac{1}{3}\right)^{3}=$
10
25

What do you notice about the values as n gets larger? How can you use this table to predict the value of the expression when n=100 and n=1,000?

As n approaches positive infinity, $\ \left(1+\frac{1}{n}\right)^{n}$ approaches 2.718281828459.

You can see that the value of this expression will never reach 3, but rather the 2.718... number above. This number has a special name: e.

The Number e

e is the number that $\ \left(1+\frac{1}{n}\right)^{n}$ approaches as n→ ∞. e is an irrational number that is approximated with 2.718281828459.

e is also called the natural number (or base), or the Euler number, named after the Swiss mathematician Leonhard Euler who popularized the use of the letter e for the constant.

Graphing & Simplifying

Work it Out 3

Graph the equations y=2^x and y=3^xon the same axis using a graphing utility.

Drawing on what you learned above, what would you expect the graph of y=e^x to look like?
What is the asymptote?
What is the y-intercept?
What is the domain and range?

Discussion

The graph of the two given equations is below. Given the value of e stated above, what do you think the graph of y=e^x would look like, and where would it be on this graph?

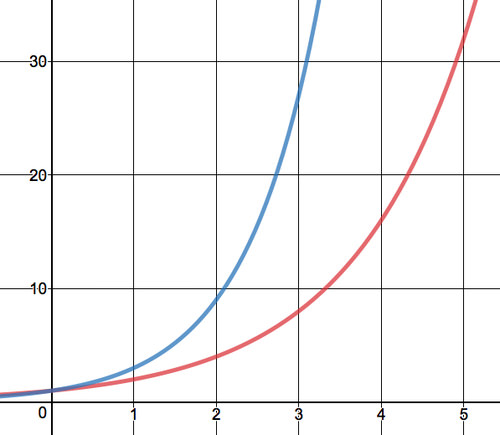
f-d_485faeeddcdc2bb77910259922afa58f36284d830eb53660dc5a5378+IMAGE_THUMB_POSTCARD_TINY+IMAGE_THUMB_POSTCARD_TINY.jpg

What do you think the asymptote for y=e^x would be given what is happening to the graph as it approaches the x-axis?

What is the value of any number raised to the 0 power? How will this help you determine the y-intercept?

How can you use this graph to determine the range (the y-values) and the domain (the x-values)?

Example 1

Simplify e²⋅e⁴.

Solution

The Laws of Exponents apply with e as a base. Because these bases are the same, you can just add the exponents. The answer is e⁶.

Using a Calculator with Logs

The value e has another common purpose: finding a log on a calculator.

You may have noticed that most calculators only have two log functions, LOG and LN.

The LOG function is actually the 'common log', log10x, and it is used in many real-world scenarios such as PH, earthquake magnitude, and sound pressure.
The LN function is the 'natural log', logex, and is used in many, many calculations involving constant growth in finance and the sciences.

In order to use these functions with other logs, first change the existing base to either 10 or e with the change of base formula:

$\ \log _{b} x=\frac{\log x}{\log b} \quad \text { OR } \quad \log _{b} x=\frac{\ln x}{\ln b}$

The change of base formula allows any base to be evaluated as base 10 or base e.

Example 2

Use a calculator and the change of base formula to determine the value of $\ \log_7247$.

Solution

First, apply the change of base formula to convert to LN or LOG (the process is the same, it just depends on the function you wish to use on the calculator):

$\ \log _{7} 247=\frac{\ln 7}{\ln 247}$

Then use the LN function to find the natural log of 7 and 247:

$\ \frac{\ln 7}{\ln 247}=\frac{2.4}{0.8} \approx 2.831$

Work it Out 4

Evaluate each log. Remember that $\ \log x=\log_{10}x$. Use a calculator as needed.

$\ \log 1 $
$\ \log 100$
$\ \ln 100$
$\ \log_3 29$
$\ \log_9 0.518$

Solving Natural log Equations

Work it Out 5

Solve the following logarithmic equation and check your answer.

$\ 3\ln(−x)−5=10$

Discussion

First, add 5 to both sides and then divide by 3 to isolate the natural log. Recall that the inverse of the natural log is the natural number. Therefore, everything needs to be put into the exponent of e in order to get rid of the log.

Example 3

Rewrite the following expression under a single log.

$\ \ln e−\ln4x+2(e^{\ln x}⋅\ln5)$

Solution

Apply the properties of logarithms:

$\ \begin{aligned}
\ln e-\ln 4 x+2\left(e^{\ln x} \cdot \ln 5\right) &=\ln \left(\frac{e}{4 x}\right)+2 x \cdot \ln 5 \\
&=\ln \left(\frac{e}{4 x}\right)+\ln \left(5^{2 x}\right) \\
&=\ln \left(\frac{e \cdot 5^{2 x}}{4 x}\right)
\end{aligned}$

Example 4

Solve: $\ \ln(x−1)−\ln(x+1)=8$.

Solution

Start by condensing the left-hand side using the Quotient Rule. Because this problem involves natural logs, you'll need to put everything in the exponent of e.

$\ \begin{aligned}
\ln (x-1)-\ln (x+1) &=8 \\
\ln \left(\frac{x-1}{x+1}\right) &=8 \\
\frac{x-1}{x+1} &=e^{8} \\
x-1 &=(x+1) e^{8} \\
x-1 &=x e^{8}+e^{8} \\
x-x e^{8} &=1+e^{8} \\
x\left(1-e^{8}\right) &=1+e^{8} \\
x &=\frac{1+e^{8}}{1-e^{8}} \approx-1.0007
\end{aligned}$

The solution is approximately -1.0007, which you can check by plugging it back into the equation. You will end up with ln(−1.0007−1)−ln(−1.0007+1)=8, and because you cannot take the log of a negative number, there is no solution for this equation. If you graph the left side and the right side, you can also see that there is no solution.

Continuous Exponential Growth & Decay

Example 5

The interest on a sum of money that compounds continuously can be calculated with the formula I=Pe^rt−P, where P is the amount invested (the principal), r is the interest rate, and t is the amount of time the money is invested. If you invest $1,000 in a bank account that pays 2.5% interest compounded continuously and you leave the money in that account for 4 years, how much interest will you earn?

Solution

Plug the given values into the equation I=Pe^rt−P and solve for I.

$\ \begin{array}{l}
I=P e^{r t}-P \\
I=1000 \cdot e^{0.025 \cdot 4}-1000 \\
I=1000 \cdot e^{0.1}-1000 \\
I=1000 \cdot 1.10517-1000 \\
I=1105.17-1000 \\
I=105.17
\end{array}$

Therefore, at the end of 4 years, you will have earned $105.17 in interest.

Work it Out 6

Gianna opens a savings account with $1,000 and it accrues interest continuously at a rate of 5%. What is the balance in the account after 6 years?

Discussion

This example builds off of Active Learning 1. Here, the interest compounds continuously, which is different from word problems that involve interest compounding monthly, quarterly, annually, etc. (in other words, at defined intervals). The equation changes slightly, from $\ A=P\left(1+\frac{r}{n}\right)^{n t} \text { to } A=P e^{r t}$, without n, because there is no longer any interval.

What is the equation for this scenario? How can you use the equation to determine the balance in the account after 6 years?

Work it Out 7

Determine if $\ y=\frac{1}{2} e^{x}$ represents exponential growth, decay, or neither.

Discussion

Recall that to be exponential growth, the base must be greater than one. To be exponential decay, the base must be between zero and one.

Therefore, is this a growth equation, a decay equation, or neither? Why?

Work it Out 8

The rate of radioactive decay of radium is modeled by R=Pe^−0.00043t, where R is the amount (in grams) of radium present after t years and P is the initial amount (also in grams). If there is 698.9 grams of radium present after 5,000 years, what was the initial amount?

Discussion

How can you use the formula given in the problem to write an equation? What steps are needed to solve the equation for P?

* Interactive

Review

Determine if the following functions are exponential growth, decay or neither. Give a reason for your answer.

$\ y=\frac{4}{3} e^{x}$
$\ y=\left(\frac{1}{e}\right)^{x}+2$

Simplify the following expressions with e.

$\ e^{-3} \cdot e^{12}$
$\ \frac{5 e^{-4}}{e^{3}}$
$\ \left(\frac{4 e^{4}}{3 e^{-2} e^{3}}\right)^{-2}$

Solve the following word problems.

The population of Springfield is growing exponentially. The growth can be modeled by the function P=Ie^0.055t, where P represents the projected population, I represents the current population of 100,000 in 2012 and t represents the number of years after 2012.

Graph this equation.
To the nearest person, what will the population be in 2022?
In what year will the population double in size if this growth rate continues?

The value of Steve’s car decreases in value according to the exponential decay function: V=Pe^−0.12t, where V is the current value of the vehicle, t is the number of years Steve has owned the car and P is the purchase price of the car, $25,000.

To the nearest dollar, what will the value of Steve’s car be in 2 years?
To the nearest dollar, what will the value be in 10 years?

Naya invests $5,000 in an account which accrues interest monthly at a rate of 2%.

Write an exponential growth function to model the value of her investment after t years.
How much total interest does Naya earn in the first eight months to the nearest dollar?
How much money, to the nearest dollar, is in the account after 3 years?

Malcolm invests $7,500 in an account which accrues interest continuously at a rate of 4.5%.

Write an exponential growth function to model the value of his investment after t years.
How much interest does Malcolm earn in the first six months to the nearest dollar?
How much money, to the nearest dollar, is in the account after 8 years?

Work it Out

n	\(\ \left(1+\frac{1}{n}\right)^{n}\)
1	\(\ \left(1+\frac{1}{1}\right)^{1}=2\)
2	\(\ \left(1+\frac{1}{2}\right)^{2}=2.25\)
3	\(\ \left(1+\frac{1}{3}\right)^{3}=\)
10
25