Skip to main content
K12 LibreTexts

4.4.1: Polar Coordinates

  1. Last updated
  2. Save as PDF
  • Page ID
    14428

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Polar Coordinates

    Everyone has dreamed of flying at one time or another. Not only would there be much less traffic to worry about, but directions would be so much simpler!

    Walking or driving: "Go East 2 blocks, turn left, then North 6 blocks. Wait for the train. Turn right, East 3 more blocks, careful of the cow! Turn left, go North 4 more blocks and park."

    Flying: "Fly 30 deg East of North for a little less than 11 and 1/4 blocks. Land."

    Nice daydream, but what does it have to do with polar coordinates?

    Polar Coordinates

    The polar coordinate system is an alternative to the Cartesian coordinate system you have used in the past to graph functions. The polar coordinate system is specialized for visualizing and manipulating angles.

    Angles are identified by travelling counter-clockwise around the circular graph from the 0 deg line, or r-axis (where the + x axis would be) to a specified angle.

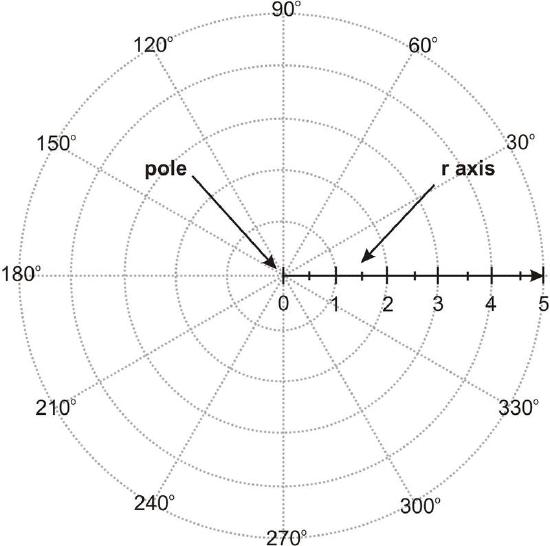    f-d_ccdf27d83e18011dad541a377ca59488bc86cc410551a70581eb79a9+IMAGE_TINY+IMAGE_TINY.jpg[Figure1]

    To plot a specific point, first go along the r-axis by r units. Then, rotate counterclockwise by the given angle, commonly represented "θ". Be careful to use the correct units for the angle measure (either radians or degrees).

    Radians

    Usually polar plots are done with radians (especially if they include trigonometric functions), but sometimes degrees are used.

    A radian is the angle formed between the r axis and a polar axis drawn to meet a section of the circumference that is the same length as the radius of a circle.

    Given that the circumference of a circle is 2π⋅r, and since r is the radius, that means there are 2π radians in a complete circle, and 1π radians in 1/2 of a circle.

    If 1/2 of a circle is π radians, and is 180 deg, that means that there are \(\ \frac{180}{\pi}\) degrees in each radian.

    That translates to approximately 57.3 degrees = 1 radian.

    Graphing Using Technology

    Polar equations can be graphed using a graphing calculator: With the graphing calculator- go to MODE. There select RADIAN for the angle measure and POL (for Polar) on the FUNC (function)line. When Y = is pressed, note that the equation has changed from y = to r = . There input the polar equation. After pressing graph, if you can’t see the full graph, adjust x- and y- max/min, etc in WINDOW.

    " frameborder="0" height="450px" name="92048" src="https://www.ck12.org/flx/show/video/...nates-Overview" thumbnailurl="" title="VideoObject?hash=1a6cbeee9e3598a31394e80c1e6462fd" uploaddate="2016-07-06 23:19:25" width="95%">

    Examples

    Example 1

    Plot the points on a polar coordinate graph: Point A \(\ \left(2, \frac{\pi}{3}\right)\), Point B (4, 135o), and Point C \(\ \left(-2, \frac{\pi}{6}\right)\)

    Solution

    Below is the pole, polar axis and the points A, B and C.

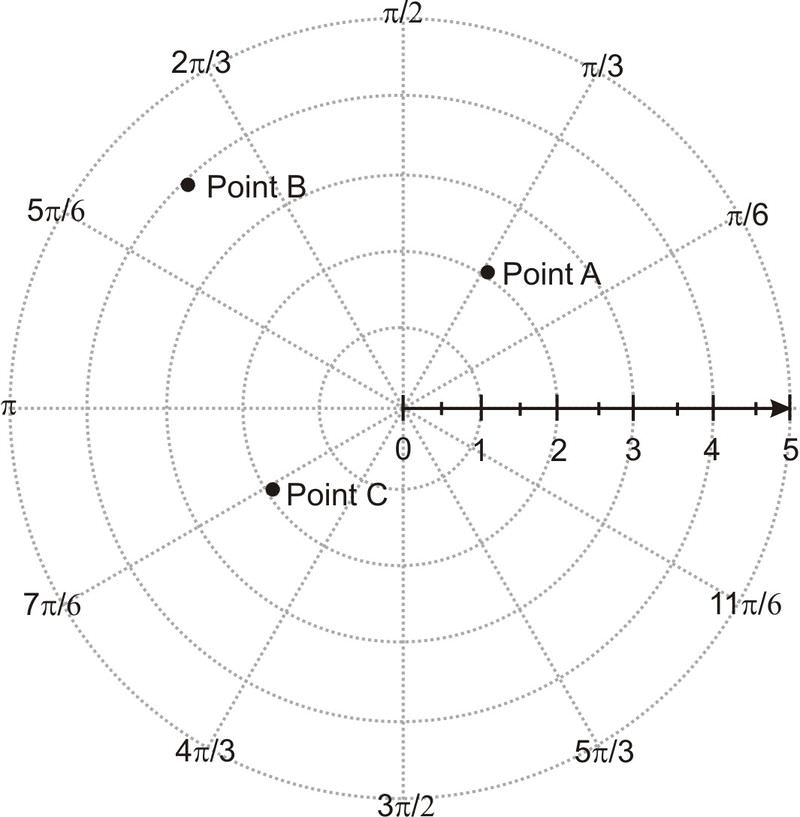    f-d_45279c3164d72aea30bc907cc78577f3a446b590a7603563de5b25bc+IMAGE_TINY+IMAGE_TINY.jpg[Figure2]
    Example 2

    Plot the following points.

    1. (4, 30o)
    2. (2.5, \(\ \pi\))
    3. \(\ \left(-1, \frac{\pi}{3}\right)\)
    4. \(\ \left(3, \frac{5 \pi}{6}\right)\)
    5. (−2, 300o)

    Solution

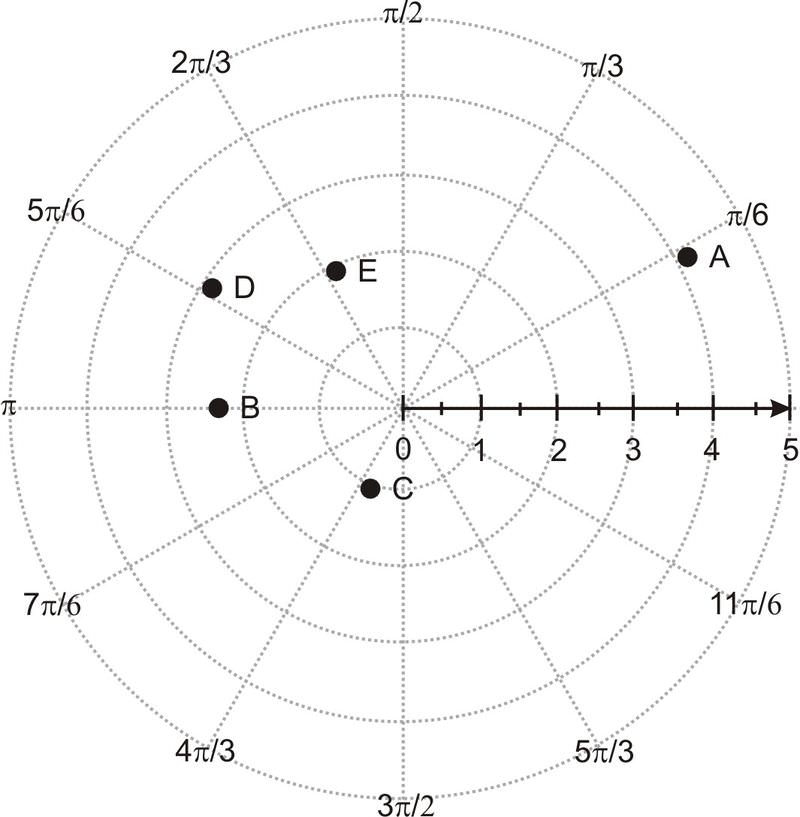    f-d_9a4a1287ccf13fafa4f8118fc75ca57e906af30dff296f3ee0c7504c+IMAGE_TINY+IMAGE_TINY.jpg[Figure3]
    Example 3

    Use a graphing calculator or plotting program to plot the following equations.

    1. r=1+3sinθ
    2. r=1+2cosθ

    Solution

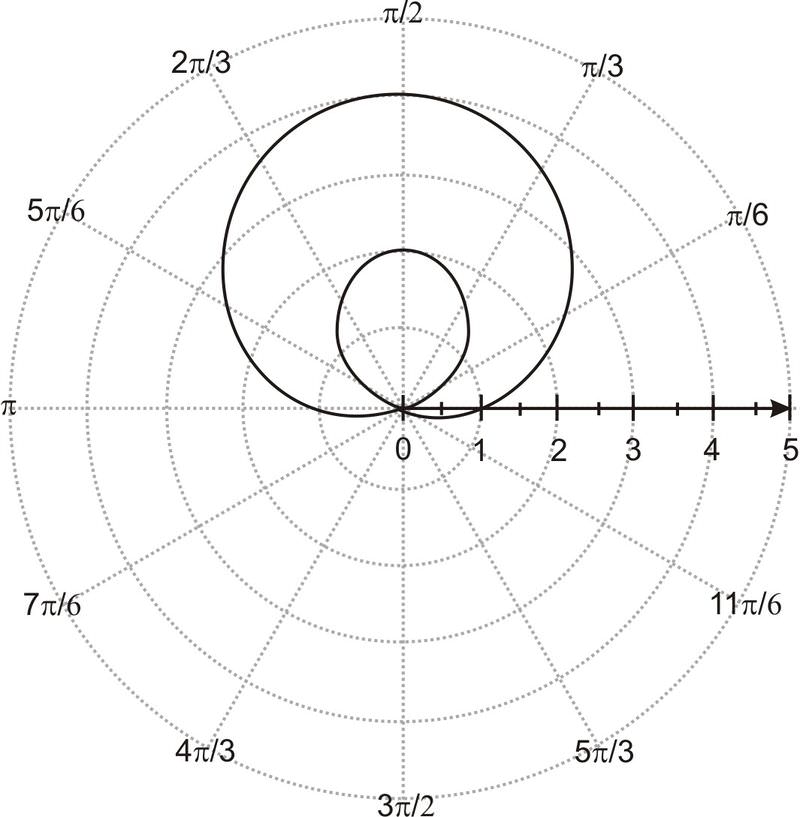
    1. f-d_86957457d9f2f7c34991ba3bdf2a548a7954527e8b5f5f729b738235+IMAGE_TINY+IMAGE_TINY.jpg
    2. Review the steps above under graphing using technology if you are having trouble.
    Example 4

    Convert from radians to degrees.

    Recall that \(\ \pi r a d=180^{\circ} \text { and } 1 \mathrm{rad}=\frac{180}{\pi} \approx 57.3^{\circ}\)

    1. \(\ \frac{\pi}{2}\)
    2. 5.17
    3. \(\ \frac{3 \pi}{2}\)

    Solution

    1. If \(\ \pi r a d=180^{\circ}\) then \(\ \frac{\pi}{2} r a d=90^{\circ}\)
    2. If \(\ 1 rad \approx 57.3^{\circ}\) then \(\ 5.17 rad \approx 296^{\circ}\)
    3. If \(\ \pi r a d=180^{\circ}\) then \(\ \frac{3 \pi}{2} r a d=270^{\circ}\)
    Example 5

    Convert from degrees to radians.

    Recall that \(\ \frac{180^{\circ}}{\pi}=57.3^{\circ} \approx 1 \mathrm{rad}\).

    1. 251o
    2. 360o
    3. 327o

    Solution

    1. If \(\ 57.3^{\circ} \approx 1rad\) then \(\ 251^{\circ} \approx 4.38 \mathrm{rad} \approx 1.4 \pi \mathrm{rad}\)
    2. If \(\ 57.3^{\circ} \approx 1 rad\) then \(\ 360^{\circ} \approx 6.28 rad\)
    3. If \(\ 57.3^{\circ} \approx 1 rad\) then \(\ \frac{327^{\circ}}{57.3^{\circ}} \approx 5.71 rad\)
    Example 6

    Convert from degrees to radians, answer in terms of π.

    Recall that 2πrad=360o and therefore πrad=180o.

    1. 90o
    2. 270o
    3. 45o

    Solution

    1. If \(\ \pi r a d=180^{\circ}\) then \(\ \frac{\pi}{2} r a d=90^{\circ}\)
    2. If \(\ \pi r a d=180^{\circ} \text { and } \frac{\pi}{2} r a d=90^{\circ}\) then \(\ 1 \frac{1}{2} \pi r a d \rightarrow \frac{3}{2} \pi \rightarrow \frac{3 \pi}{2} r a d=270^{\circ}\)
    3. If \(\ \frac{\pi}{2} r a d=90^{\circ}\) then \(\ \frac{\pi}{4} r a d=45^{\circ}\)

    Review

    1. Why can a point on the plane not be labeled using a unique ordered pair (r, θ).
    2. Explain how to graph (r, θ) if r<0 and/or θ>360.

    Graph each point on the polar plane.

    1. \(\ \text{A}\left(6,145^{\circ}\right)\)
    2. \(\ \text{B} (-2, \frac{13\pi}{6})\)
    3. \(\ \text{C} (\frac{7}{4}, -210^{\circ})\)
    4. \(\ \text{D}(5, \frac{\pi}{2})\)
    5. \(\ \text{E}(3.5, \frac{-\pi}{8})\)

    Name two other pairs of polar coordinates for each point.

    1. \(\ (1.5, 170^{\circ})\)
    2. \(\ (-5, \frac{\pi}{-3})\)
    3. \(\ (3, 305^{\circ})\)

    Graph each polar equation.

    1. \(\ r=3\)
    2. \(\ \theta=\frac{\pi}{5}\)
    3. \(\ r=15.5\)
    4. \(\ r=1.5\)
    5. \(\ \theta=-175^{\circ}\)

    Find the distance between the given points.

    1. \(\ P_{1}\left(5, \frac{\pi}{2}\right) \text { and } P_{2}\left(7, \frac{3 \pi}{9}\right)\)
    2. \(\ P_{1}\left(1.3,-52^{o}\right) \text { and } P_{2}\left(-13.6,-162^{\circ}\right)\)
    3. \(\ P_{1}\left(3,250^{\circ}\right) \text { and } P_{2}\left(7,90^{\circ}\right)\)

    Review (Answers)

    To see the Review answers, open this PDF file and look for section 4.1.

    Vocabulary

    Term Definition
    \(\ \pi\) \(\ \pi\) (Pi) is the ratio of the circumference of a circle to its diameter. It is an irrational number that is approximately equal to 3.14.
    Cartesian coordinate system The Cartesian plane is a grid formed by a horizontal number line and a vertical number line that cross at the (0, 0) point, called the origin.
    polar axis The polar axis is a ray drawn from the pole at the 0∘ angle on a polar graph.
    polar coordinate system The polar coordinate system is a special coordinate system in which the location of each point is determined by its distance from the pole and its angle with respect to the polar axis.
    pole The pole is the center point on a polar graph.
    radian A radian is a unit of angle that is equal to the angle created at the center of a circle whose arc is equal in length to the radius.

    This page titled 4.4.1: Polar Coordinates is shared under a CK-12 license and was authored, remixed, and/or curated by CK-12 Foundation via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.

    CK-12 Foundation
    LICENSED UNDER
    CK-12 Foundation is licensed under CK-12 Curriculum Materials License
    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
      Author
      CK12
      License
      CK-12
      OER program or Publisher
      CK-12
    2. Tags
      1. source@https://www.ck12.org/c/analysis