4.5.7: Powers and Roots of Complex Numbers

Powers and Roots of Complex Numbers

Manually calculating (simplifying) a statement such as: \(\ (14-17 i)^{5}\) or \(\ \sqrt[4]{(3-2 i)}\) in present (rectangular) form would be a very intensive process at best.

Fortunately you will learn in this lesson that there is an alternative: De Moivre's theorem. De Moivre's theorem is really the only practical method for finding the powers or roots of a complex number, but there is a catch...

What must be done to a complex number before De Moivre's theorem can be utilized?

---

Powers and Roots of Complex Numbers

Powers of Complex Numbers

How do we raise a complex number to a power? Let’s start with an example:

\(\ (-4-4 i)^{3}=(-4-4 i) \cdot(-4-4 i) \cdot(-4-4 i)\)

In rectangular form, this can get very complex. What about in r cis θ form?

\(\ (-4-4 i)=4 \sqrt{2} \operatorname{cis}\left(\frac{5 \pi}{4}\right)\)

and using our multiplication rule from the previous section,

\(\ (-4-4 i)^{3}=(4 \sqrt{2})^{3} \operatorname{cis}\left(\frac{15 \pi}{4}\right)\)

Notice, \(\ (a+b i)^{3}=r^{3} \text { cis } 3 \theta\)

In words: Raise the r-value to the same degree as the complex number is raised and then multiply that by cis of the angle multiplied by the number of the degree.

Reflecting on the example above, we can identify De Moivre's Theorem:

Let z = r(cos θ + i sin θ) be a complex number in rcisθ form. If n is a positive integer, zⁿ is zⁿ = rⁿ (cos(nθ) + i sin(nθ))

It should be clear that the polar form provides a much faster result for raising a complex number to a power than doing the problem in rectangular form.

Roots of Complex Numbers

You probably noticed long ago that when an new operation is presented in mathematics, the inverse operation often follows. That is generally because the inverse operation is often procedurally similar, and it makes good sense to learn both at the same time.

This is no exception:

The inverse operation of finding a power for a number is to find a root of the same number.

1. Recall from algebra that any root can be written as \(\ x^{1 / n}\)
2. Given that the formula for De Moivre’s theorem also works for fractional powers, the same formula can be used for finding roots:

   \(\ z^{1 / n}=(a+b i)^{1 / n}=r^{1 / n} \operatorname{cis}\left(\frac{\theta}{n}\right)\)

---

Examples

Example 1

Earlier, you were asked what should be done to a complex number before you can use De Moivre's theorem on it.

Solution

A complex number operation written in rectangular form, such as: (13−4i)³ must be converted to polar form before utilizing De Moivre's theorem.

Example 2

Find the value of \(\ (1+\sqrt{3} i)^{4}\).

Solution

\(\ \begin{array}{l}
r=\sqrt{(1)^{2}+(\sqrt{3})^{2}}=2 \\
\tan \theta_{r e f}=\frac{\sqrt{3}}{1}
\end{array}\)

and θ is in the 1^st quadrant, so

\(\ \theta=\frac{\pi}{3}\)

Using our equation from above:

\(\ \begin{array}{l}
z^{4}=r^{4} \text { cis } 4 \theta \\
z^{4}=(2)^{4} \text { cis } 4 \frac{\pi}{3}
\end{array}\)

Expanding cis form:

\(\ \begin{array}{l}
z^{4}=16\left(\cos \left(\frac{4 \pi}{3}\right)+i \sin \left(\frac{4 \pi}{3}\right)\right) \\
=16((-0.5)-0.866 i)
\end{array}\)

Finally we have

\(\ z^{4}=-8-13.856 i\)

Example 3

Find \(\ \sqrt{1+i}\).

Solution

First, rewriting in exponential form: \(\ (1+i)^{1 / 2}\)

And now in polar form:

\(\ \sqrt{1+i}=\left(\sqrt{2} \operatorname{cis}\left(\frac{\pi}{4}\right)\right)^{1 / 2}\)

Expanding cis form,

\(\ =\left(\sqrt{2}\left(\cos \left(\frac{\pi}{4}\right)+i \sin \left(\frac{\pi}{4}\right)\right)\right)^{1 / 2}\)

Using the formula:

\(\ \begin{array}{l}
=\left(2^{1 / 2}\right)^{1 / 2}\left(\cos \left(\frac{1}{2} \cdot \frac{\pi}{4}\right)+i \sin \left(\frac{1}{2} \cdot \frac{\pi}{4}\right)\right) \\
=2^{1 / 4}\left(\cos \left(\frac{\pi}{8}\right)+i \sin \left(\frac{\pi}{8}\right)\right)
\end{array}\)

In decimal form, we get

\(\ \begin{array}{l}
=1.189(0.924+0.383 i) \\
=1.099+0.455 i
\end{array}\)

To check, we will multiply the result by itself in rectangular form:

\(\ \begin{array}{l}
(1.099+0.455 i) \cdot(1.099+0.455 i)=1.099^{2}+1.099(0.455 i)+1.099(0.455 i)+(0.455 i)^{2} \\
=1.208+0.500 i+0.500 i+0.208 i^{2} \\
=1.208+i-0.208 \text { or } \\
=1+i
\end{array}\)

Example 4

Find the value of \(\ x: x^{3}=(1-\sqrt{3} i)\)

Solution

First we put \(\ 1-\sqrt{3} i\) in polar form.

Use \(\ x=1, y=-\sqrt{3}\) to obtain \(\ r=2, \theta=\frac{5 \pi}{3}\)

let \(\ z=(1-\sqrt{3} i)\) in rectangular form

\(\ z=2 \operatorname{cis}\left(\frac{5 \pi}{3}\right)\) in polar form

\(\ x=(1-\sqrt{3} i)^{1 / 3}\)

\(\ x=\left[2 \operatorname{cis}\left(\frac{5 \pi}{3}\right)\right]^{1 / 3}\)

Use De Moivre’s theorem to find the first solution:

\(\ x_{1}=2^{1 / 3} \operatorname{cis}\left(\frac{5 \pi / 3}{3}\right) \text { or } 2^{1 / 3} \operatorname{cis}\left(\frac{5 \pi}{9}\right)\)

Leave answer in cis form to find the remaining solutions:

n = 3 which means that the 3 solutions are \(\ \frac{2 \pi}{3}\) radians apart or

\(\ x_{2}=2^{1 / 3} \operatorname{cis}\left(\frac{5 \pi}{9}+\frac{2 \pi}{3}\right)\) and \(\ x_{3}=2^{1 / 3} \operatorname{cis}\left(\frac{5 \pi}{9}+\frac{2 \pi}{3}+\frac{2 \pi}{3}\right)\)

Note

It is not necessary to add \(\ \frac{2 \pi}{3}\) again. Adding \(\ \frac{2 \pi}{3}\) three times equals \(\ 2 \pi\). That would result in rotating around a full circle and to start where it all began- that is the first solution.

The three solutions are:

\(\ \begin{array}{l}
x_{1}=2^{1 / 3} \operatorname{cis}\left(\frac{5 \pi}{9}\right) \\
x_{2}=2^{1 / 3} \operatorname{cis}\left(\frac{11 \pi}{9}\right) \\
x_{3}=2^{1 / 3} \operatorname{cis}\left(\frac{17 \pi}{9}\right)
\end{array}\)

Each of these solutions, when graphed will be \(\ \frac{2 \pi}{3}\) apart.

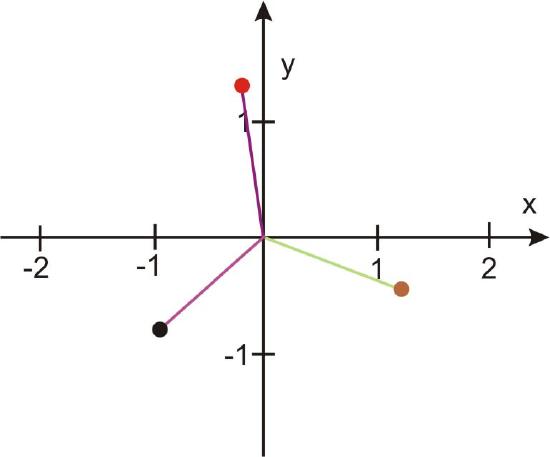
Check any one of these solutions to see if the results are confirmed.

Checking the second solution:

\(\ \begin{array}{l}
x_{2}=2^{1 / 3} \operatorname{cis}\left(\frac{11 \pi}{9}\right) \\
=1.260\left[\cos \left(\frac{11 \pi}{9}\right)+i \sin \left(\frac{11 \pi}{9}\right)\right] \\
=1.260[-0.766-0.643 i] \\
=-0.965-0.810 i \\
\text { Does }(-0.965-0.810 i)^{3} \text { or }(-0.965-0.810 i)(-0.965-0.810 i)(-0.965-0.810 i) \\
=(1-\sqrt{3} i) ?
\end{array}\)

Example 5

What are the two square roots of i?

Solution

Let \(\ z=\sqrt{0+i}\).

\(\ r=1, \theta=\pi / 2 \text { or } z=\left[1 \times \operatorname{cis} \frac{\pi}{2}\right]^{1 / 2}\) Utilizing De Moivre’s theorem:

\(\ z_{1}=\left[1 \times \operatorname{cis} \frac{\pi}{4}\right] \text { or } z_{2}=\left[1 \times \operatorname{cis} \frac{5 \pi}{4}\right]\)

\(\ z_{1}=1\left(\cos \frac{\pi}{4}+i \sin \frac{\pi}{4}\right) \text { or } z_{2}=1\left(\cos \frac{5 \pi}{4}+i \sin \frac{5 \pi}{4}\right)\)

\(\ z_{1}=0.707+0.707 i \text { or } z_{2}=-0.707-0.707 i\)

Check for z₁ solution: \(\ (0.707+0.707 i)^{2}=i ?\)

\(\ 0.500+0.500 i+0.500 i+0.500 i^{2}=0.500+i+0.500(-1) \text { or } i\)

Example 6

Calculate \(\ \sqrt[4]{(1+0 i)}\). What are the four fourth roots of 1?

Solution

Let \(\ z=1 \text { or } z=1+0 i\). Then the problem becomes find \(\ z^{1 / 4}=(1+0 i)^{1 / 4}\).

Since \(\ r=1 \theta=0, z^{1 / 4}=[1 \times \operatorname{cis} 0]^{1 / 4}\) with \(\ z_{1}=1^{1 / 4}\left(\cos \frac{0}{4}+i \sin \frac{0}{4}\right)\) or \(\ 1(1+0)\) or \(\ 1\)

That root is not a surprise. Now use De Moivre’s to find the other roots:

\(\ z_{2}=1^{1 / 4}\left[\cos \left(0+\frac{\pi}{2}\right)+i \sin \left(0+\frac{\pi}{2}\right)\right]\) Since there are 4 roots, dividing \(\ 2 \pi\) by 4 yields \(\ 0.5 \pi\) or \(\ 0+i\) or just \(\ i\) \(\ z_{3}=1^{1 / 4}\left[\cos \left(0+\frac{2 \pi}{2}\right)+i \sin \left(0+\frac{2 \pi}{2}\right)\right]\) which yields \(\ z_{3}=-1\)

Finally, \(\ z_{4}=1^{1 / 4}\left[\cos \left(0+\frac{3 \pi}{2}\right)+i \sin \left(0+\frac{3 \pi}{2}\right)\right]\) or \(\ z_{4}=-i\)

The four fourth roots of 1 are 1, i, -1 and -i.

Example 7

Calculate \(\ (\sqrt{3}+i)^{7}\).

Solution

To calculate \(\ (\sqrt{3}+i)^{7}\) start by converting to rcis form.

First, find r. Recall \(\ r=\sqrt{\sqrt{3}^{2}+1^{2}}\).

\(\ \begin{array}{l}
r=\sqrt{3+1} \\
r=2
\end{array}\)

If \(\ \cos \theta=\frac{\sqrt{3}}{2}\) and \(\ \sin \theta=\frac{1}{2}\) then \(\ \theta=30^{\circ}\) and is in quadrant I. Now that we have trigonometric form, the rest is easy:

\(\ (\sqrt{3}+i)^{7}=\left[2\left(\cos 30^{\circ}+i \sin 30^{\circ}\right)\right]^{7}\)..... Write the original problem in rcis form

\(\ 2^{7}\left[\left(\cos \left(7 \cdot 30^{\circ}\right)+i \sin \left(7 \cdot 30^{\circ}\right)\right]\right.\)..... De Moivre's theorem

\(\ 128\left[-\frac{\sqrt{3}}{2}+\frac{-1}{2} i\right]\)..... Simplify

\(\ (\sqrt{3}+i)^{7}=-64 \sqrt{3}-64 i\)..... Simplify again

\(\ \therefore(\sqrt{3}+i)^{7}=-64 \sqrt{3}-64 i\)

---

Review

Perform the indicated operation on these complex numbers:

1. Divide: \(\ \frac{2+3 i}{1-i}\)
2. Multiply: \(\ (-6-i)(-6+i)\)
3. Multiply: \(\ \left(\frac{\sqrt{3}}{2}-\frac{1}{2} i\right)^{2}\)
4. Find the product using polar form: \(\ (2+2 i)(\sqrt{3}-i)\)
5. Multiply: \(\ 2\left(\cos 40^{\circ}+i \sin 40^{\circ}\right) \cdot 4\left(\cos 20^{\circ}+i \sin 20^{\circ}\right)\)
6. Multiply: \(\ 2\left(\cos \frac{\pi}{8}+i \sin \frac{\pi}{8}\right) \cdot 2\left(\cos \frac{\pi}{10}+i \sin \frac{\pi}{10}\right)\)
7. Divide: \(\ 2\left(\cos 80^{\circ}+i \sin 80^{\circ}\right) \div 6\left(\cos 200^{\circ}+i \sin 200^{\circ}\right)\)
8. Divide: \(\ 3 \operatorname{cis}\left(130^{\circ}\right) \div 4 \operatorname{cis}\left(270^{\circ}\right)\)

Use De Moivre’s theorem.

9. \(\ \left[3\left(\cos 80^{\circ}+i \sin 80^{\circ}\right)\right]^{3}\)
10. \(\ \left[\sqrt{2}\left(\cos \frac{5 \pi}{16}+i \sin \frac{5 \pi}{16}\right)\right]^{4}\)
11. \(\ (\sqrt{3}-i)^{6}\)
12. Identify the 3 complex cube roots of \(\ 1+i\)
13. Identify the 4 complex fourth roots of \(\ -16 i\)
14. Identify the five complex fifth roots of \(\ i\)

---

Review (Answers)

To see the Review answers, open this PDF file and look for section 4.10.

---

Vocabulary

Term	Definition
complex number	A complex number is the sum of a real number and an imaginary number, written in the form a+bi.
De Moivre's Theorem	De Moivre's theorem is the only practical manual method for identifying the powers or roots of complex numbers. The theorem states that if z=r(cosθ+isinθ) is a complex number in rcisθ form and n is a positive integer, then z^n=r^n(cos(nθ)+isin(nθ)).