1.1.2: Intervals and Interval Notation
- Page ID
- 14123
Intervals and Interval Notation
Suppose you and 2 of your friends were out for lunch and decide to buy tacos. Together you have $15 to spend on lunch, and tacos are $1.25 each. It is clear that the total cost could be graphed as a function of the number of tacos purchased, but how would you specify that the graph should not include values greater than $15 or less than $3.75 (one taco each)?
Intervals and Interval Notation
A function is defined as a real function if both the domain and the range are sets of real numbers. Many of the functions you have likely encountered before are real functions, and many of these functions have Domain=ℝ. Consider, for example, the function y=3x. A section of the graph of this function is shown below.
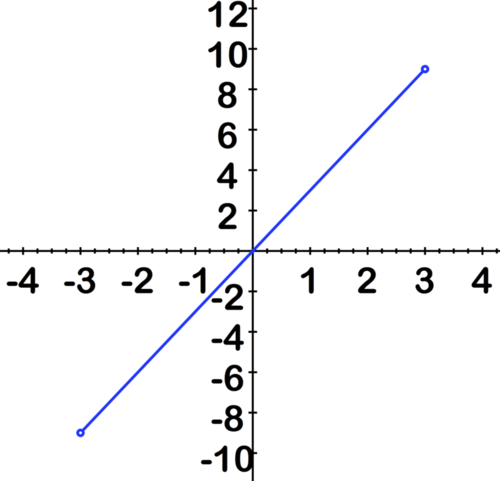 [Figure1]
[Figure1]You may already be familiar with the graphs of lines. In particular, you may already be in the habit of placing arrows at the ends. We do this in order to indicate that the line will continue forever in both the positive and negative directions, both in terms of the domain and the range. The line above, however, only shows the function y=3x on the interval [-3, 3]. The square brackets indicate that the graph includes the endpoints of the interval, where x=−3 and x=3. We call this a closed interval. A closed interval contains its endpoints. In contrast, an open interval does not contain its endpoints. We indicate an open interval with parentheses. For example, (-3, 3) indicates the set of numbers between -3 and 3, not including -3 and 3. You may have noticed that the open interval notation looks like the notation for a point (x,y) in the plane. It is important to read an example or a homework problem carefully to avoid confusing a point with an interval! The difference is generally quite clear from the context.
The table below summarizes the kinds of intervals you may need to consider while studying functions and their domains (and ranges):
|
Interval notation |
Inequality notation |
Description |
|
[a,b] |
a≤x≤b |
The value of x is between a and b, including a and b, where a, b are real numbers. |
|
(a,b) |
a<x<b |
The value of x is between a and b, not including a and b. |
|
[a,b) |
a≤x<b |
The value of x is between a and b, including a, but not including b. |
|
(a,b] |
a<x≤b |
The value of x is between a and b, including b, but not including a. |
|
(a,∞) |
x>a |
The value of x is strictly greater than a. |
|
[a,∞) |
x≥a |
The value of x is greater than or equal to a. |
|
(−∞,a) |
x |
The value of x is strictly less than a. |
|
(−∞,a] |
x≤a |
The value of x is less than or equal to a. |
Using the table above, you can identify the sets following three sets:
- (−3,9]
- [−23,12]
- (−∞,0)
The set (−3,9] describes the set of numbers between -3 and 9, “not including” the actual value of -3, but “including” 9.
The set [−23,12] describes the set of numbers between -23 and 12, “including” the values -23 and 12.
The set (−∞,0) describes all numbers less than 0, not including 0 itself.
When asked to graph a function on a given interval, be careful to restrict the graph to the interval. Take the following function f(x)=\(\ 1 \over 2\)x−6 on the interval [-4, 12]. The graph is:
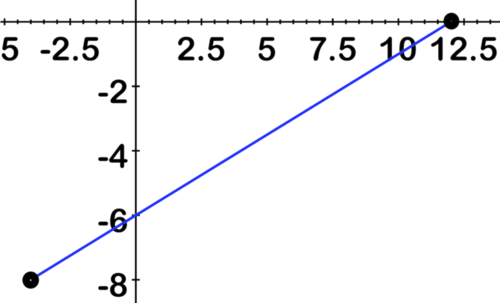 [Figure2]
[Figure2]The part of the function that is graphed is the line between -4 and 12 with -4 and 12 included.
Examples
Earlier, you were asked about how to specify the cost of lunch for you and your 2 friends if you have $15 together to spend and tacos are $1.25 each. The least you could spend on lunch is $3.75 which includes one taco each. To describe the only the values values between $3.75 and $15.00, specify the interval of the domain as: [3.75, 15]. Note that these are closed brackets because the values in the brackets are included.
Describe the set shown in the image using interval notation:
 [Figure3]
[Figure3]Solution
The set is opened with “(”, since neg infinity cannot be reached, then closed with “)”, since 3 is not included. The set is re-opened with “(” since 0 is not included, and finally closed with “)” since pos infinity cannot be reached either.
Describe the specified intervals, use interval notation:
Solution
- All negative numbers.
- Zero is neither positive nor negative, so the “)” is used to specify that zero is “not” included. Since there is no maximum negative number, we specify that infinity is the lower value, and use “(” since it cannot be reached.
- The numbers between five and twelve, including five, but not twelve.
- The “[” is used to open the set, since 5 is included, but “)” is used to close, since 12 is not.
- Negative numbers down to negative six, zero, and all positive numbers.
- The “(” denotes that negative infinity cannot be reached, and “]” on the other end specifies that 9 is included in the set.
Describe the domain in the sets in the graphs using interval notation:
 [Figure4]
[Figure4] [Figure5]
[Figure5]Solution
For graph 1, the domain is the set of x values starting with the included -6 and ending at 4, which is not included: [-6, 4).
For graph 2, for the same reasoning as above, the domain is [-6, 7).
Describe the range in the sets in the images in Example 4 using interval notation.
Solution
The range for graph 1 is the set of y values from -3 (not included) to 4 (included): (-3, 4]
The range for graph 2 is: [-1, 6)
Review
For #1-4, write the inequality in interval notation.
- −3≤x<1
- 0<x<2
- x>−3
- x≤2
For #5-6, solve and put your answer in interval notation.
- −2x+3<1
- 7x+4≤2x−6
For #7-10, write the given set of numbers in interval notation.
7.
 [Figure6]
[Figure6]8.
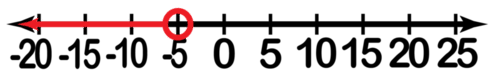 [Figure7]
[Figure7]9.
 [Figure8]
[Figure8]10.
 [Figure9]
[Figure9]For #11-12, name the domain and range for each relation using interval notation.
11.
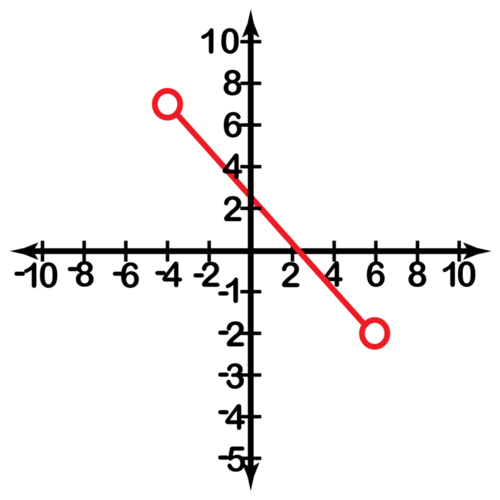 [Figure10]
[Figure10]12.

For #13-16, express in interval notation and then sketch them on a number line.
- {x:−1≤x≤3}
- {x:−2≤x<1}
- A is the set of all numbers bigger than 2 but less than or equal to 5.
- {x:−3<x<∞}
Review (Answers)
To see the Review answers, open this PDF file and look for section 1.3.
Vocabulary
| Term | Definition |
|---|---|
| domain | The domain of a function is the set of x-values for which the function is defined. |
| Interval Notation | Interval notation is the notation [a,b), where a function is defined between a and b. Use ( or ) to indicate that the end value is not included and [ or ] to indicate that the end value is included. Never use [ or ] with infinity or negative infinity. |
| Range | The range of a function is the set of y values for which the function is defined. |
| Real Number | A real number is a number that can be plotted on a number line. Real numbers include all rational and irrational numbers. |
Image Attributions
[Figure 1]
License: CC BY-NC-SA
[Figure 2]
License: CC BY-NC-SA
[Figure 3]
License: CC BY-NC-SA
[Figure 4]
License: CC BY-NC-SA
[Figure 5]
License: CC BY-NC-SA
[Figure 6]
License: CC BY-NC-SA
[Figure 7]
License: CC BY-NC-SA
[Figure 8]
License: CC BY-NC-SA
[Figure 9]
License: CC BY-NC-SA
[Figure 10]
License: CC BY-NC-SA
[Figure 11]
License: CC BY-NC-SA

