2.3.4: Sign Test for Rational Function Graphs
- Page ID
- 14199
Sign Test for Rational Function Graphs
The asymptotes of a rational function provide a very rigid structure in which the function must live. Once the asymptotes are known you must use the sign testing procedure to see if the function becomes increasingly positive or increasingly negative near the asymptotes. A driving question then becomes how close does near need to be in order for the sign test to work?
Sign Test for Rational Functions
Consider mentally substituting the number 2.99999 into the following rational expression.
\(\ f(x)=\frac{(x-1)(x+3)(x-5)(x+10)}{(x+2)(x-4)(x-3)}\)
Without doing any of the arithmetic, simply note the sign of each term:
\(\ f(x)=\frac{(+) \cdot(+) \cdot(-) \cdot(+)}{(+) \cdot(-) \cdot(-)}\)
The only term where the value is close to zero is (x−3) but careful subtraction still indicates a negative sign. The product of all of these signs is negative. This is strong evidence that this function approaches negative infinity as x approaches 3 from the left.
Next consider mentally substituting 3.00001 and going through the same process.
\(\ f(x)=\frac{(+) \cdot(+) \cdot(-) \cdot(+)}{(+) \cdot(-) \cdot(+)}\)
The product of all of these signs is positive which means that from the right this function approaches positive infinity instead. This technique is called the sign test. The sign test is a procedure for determining only whether a function is above or below the axis at a particular value.
The sign test helps you sketch and graph a function. Look at the following function:
\(\ f(x)=\frac{1}{(x+2)^{2} \cdot(x-1)}\)
Your first step for sketching this is to identify the vertical asymptotes. The vertical asymptotes occur at x=−2 and x=1. Then, you use the asymptotes to perform a sign test. The points to use the sign testing procedure with are -2.001, -1.9999, 0.9999, 1.00001. The number of decimals does matter so long as the number is sufficiently close to the asymptote. Note that any real number squared is positive.
\(\ \begin{aligned}
f(-2.001) &=\frac{(+)}{(+) \cdot(-)}=-\\
f(-1.9999) &=\frac{(+)}{(+) \cdot(-)}=-\\
f(0.9999) &=\frac{(+)}{(+) \cdot(-)}=-\\
f(1.0001) &=\frac{(+)}{(+) \cdot(+)}=+
\end{aligned}\)
Later when you sketch everything you will use your knowledge of zeroes and intercepts. For now, focus on just the portions of the graph near the asymptotes. Note that the graph below is NOT complete.
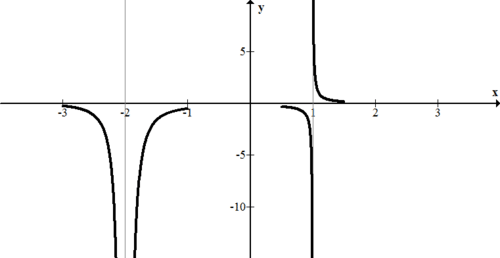 [Figure1]
[Figure1]Examples
Earlier, you were asked how close the numbers need to be to perform the sign test.
Solution
In order to truly answer the question about how close the numbers need to be, calculus should be used. For the purposes of PreCalculus, the testing number should be closer to the vertical asymptote than any other number in the problem. If the vertical asymptote occurs at 3 and 3.01 is in the problem elsewhere, do not choose 3.1 as a sign test number.
Identify the vertical asymptotes and use the sign testing procedure to roughly sketch the nature of the function near the vertical asymptotes.
\(\ f(x)=\frac{(x+1)(x-4)^{2}(x-1)(x+3)^{3}}{100(x-1)^{2}(x+2)}\)
Solution
Note that x=−2 is clearly an asymptote. It may be initially unclear whether x=1 is an asymptote or a hole. Just like holes have priority over zeroes, asymptotes have priority over holes. The four values to use the sign testing procedure are -2.001, -1.9999, 0.9999, 1.00001.
\(\ \begin{aligned}
f(-2.001) &=\frac{(-) \cdot(+) \cdot(-) \cdot(+)}{(+) \cdot(-)}=-\\
f(-1.9999) &=\frac{(-) \cdot(+) \cdot(-) \cdot(+)}{(+) \cdot(+)}=+\\
f(0.9999) &=\frac{(+) \cdot(+) \cdot(-) \cdot(+)}{(+) \cdot(+)}=-\\
f(1.0001) &=\frac{(+) \cdot(+) \cdot(+) \cdot(+)}{(+) \cdot(+)}=+
\end{aligned}\)
A sketch of the behavior of this function near the asymptotes is:
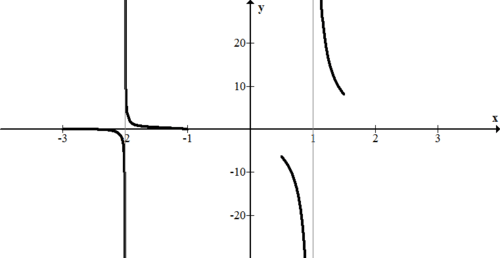 [Figure2]
[Figure2]Create a function with two vertical asymptotes at 3 and -2 such that the function approaches positive infinity from both directions at both vertical asymptotes.
Solution
Earlier, there was a function that approached negative infinity from both sides of the asymptote. This occurred because the term was squared in the denominator. An even powered term will always produce a positive term.
\(\ f(x)=\frac{1}{(x-3)^{2}(x+2)^{2}}\)
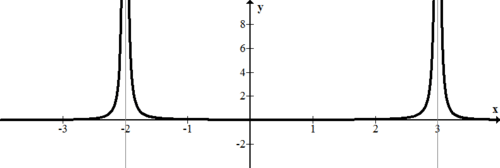 [Figure3]
[Figure3]Create a function with three vertical asymptotes such that the function approaches negative infinity for large and small values of x and has an oblique asymptote.
Solution
There are an infinite number of possible solutions. The key is to create a function that may work and then use the sign testing procedure to check. Here is one possibility.
\(\ f(x)=\frac{-x^{7}}{10(x-1)^{2}(x-2)^{2}(x-4)^{2}}\)
Identify the vertical asymptotes and use the sign testing procedure to roughly sketch the nature of the function near the vertical asymptotes.
\(\ f(x)=\frac{(x-2)^{3}(x-1)^{2}(x+1)(x+3)}{x^{3}\left(x+\frac{1}{2}\right)(x-1)(x-2)^{2}}\)
Solution
The vertical asymptotes occur at \(\ x=0,-\frac{1}{2}\). Therefore the x values to sign test are -.001, 0.001, 3.999, 4.0001.
\(\ \begin{aligned}
f(-0.001) &=+\\
f(0.001) &=-\\
f(3.999) &=-\\
f(4.0001) &=+
\end{aligned}\)
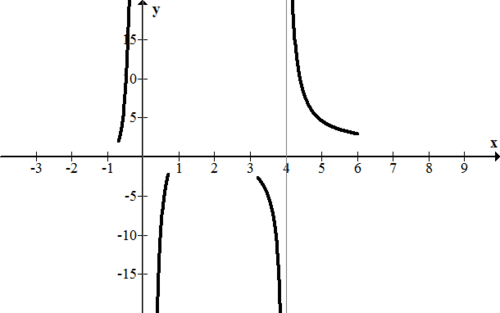 [Figure4]
[Figure4]Review
Consider the function below for questions 1-4.
\(\ f(x)=\frac{(x-2)^{4}(x+1)(x+3)}{x^{3}(x+3)(x-4)}\)
- Identify the vertical asymptotes.
- Will this function have an oblique asymptote? A horizontal asymptote? If so, where?
- What values will you need to use the sign test with in order to help you make a sketch of the graph?
- Use the sign test and sketch the graph near the vertical asymptotes.
Consider the function below for questions 5-8.
\(\ g(x)=\frac{3(x-2)^{2}(x-1)^{2}(x+1)(x+3)}{15 x^{2}(x+5)(x+1)(x-3)^{2}}\)
5. Identify the vertical asymptotes.
6. Will this function have an oblique asymptote? A horizontal asymptote? If so, where?
7. What values will you need to use the sign test with in order to help you make a sketch of the graph?
8. Use the sign test and sketch the graph near the vertical asymptote(s).
Consider the function below for questions 9-12.
\(\ h(x)=\frac{9 x^{4}-102 x^{3}+349 x^{2}-340 x+100}{x^{3}-9 x^{2}+24 x-16}\)
9. Identify the vertical asymptotes.
10. Will this function have an oblique asymptote? A horizontal asymptote? If so, where?
11. What values will you need to use the sign test with in order to help you make a sketch of the graph?
12. Use the sign test and sketch the graph near the vertical asymptotes.
Consider the function below for questions 13-16.
\(\ k(x)=\frac{2 x^{3}-5 x^{2}-11 x-4}{3 x^{3}+11 x^{2}+5 x-3}\)
13. Identify the vertical asymptotes.
14. Will this function have an oblique asymptote? A horizontal asymptote? If so, where?
15. What values will you need to use the sign test with in order to help you make a sketch of the graph?
16. Use the sign test and sketch the graph near the vertical asymptotes.
Vocabulary
| Term | Definition |
|---|---|
| End behavior | End behavior is a description of the trend of a function as input values become very large or very small, represented as the 'ends' of a graphed function. |
| Horizontal Asymptote | A horizontal asymptote is a horizontal line that indicates where a function flattens out as the independent variable gets very large or very small. A function may touch or pass through a horizontal asymptote. |
| Oblique Asymptote | An oblique asymptote is a diagonal line marking a specific range of values toward which the graph of a function may approach, but generally never reach. An oblique asymptote exists when the numerator of the function is exactly one degree greater than the denominator. An oblique asymptote may be found through long division. |
| Oblique Asymptotes | An oblique asymptote is a diagonal line marking a specific range of values toward which the graph of a function may approach, but generally never reach. An oblique asymptote exists when the numerator of the function is exactly one degree greater than the denominator. An oblique asymptote may be found through long division. |
| sign test | The sign test is a procedure for determining only whether a function is above or below the x-axis at a particular x value. The specific height is not calculated. |
| Vertical Asymptote | A vertical asymptote is a vertical line marking a specific value toward which the graph of a function may approach, but will never reach. |
Image Attributions
- [Figure 1]
Credit: CK-12 Foundation
License: CC BY-SA - [Figure 2]
Credit: CK-12 Foundation
License: CC BY-SA - [Figure 3]
Credit: CK-12 Foundation
License: CC BY-SA - [Figure 4]
Credit: CK-12 Foundation
License: CC BY-SA

