2.4.3: Horizontal Asymptotes
- Page ID
- 14203
Horizontal Asymptotes
Vertical asymptotes describe the behavior of a function as the values of x approach a specific number. Horizontal asymptotes describe the behavior of a function as the values of x become infinitely large and infinitely small. Since functions cannot touch vertical asymptotes, are they not allowed to touch horizontal asymptotes either?
Finding Horizontal Asymptotes
Horizontal asymptotes are a means of describing end behavior of a function. End behavior essentially is a description of what happens on either side of the graph as the function continues to the right and left infinitely. When you are determining the horizontal asymptotes, it is important to consider both the right and the left hand sides, because the horizontal asymptotes will not necessarily be the same in both places. Consider the reciprocal function and note how as x goes to the right and left it flattens to the line y=0.
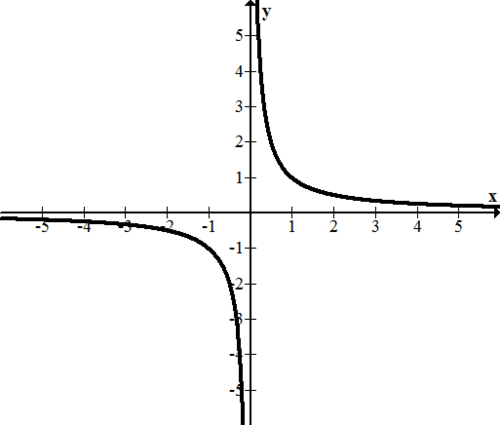 [Figure1]
[Figure1]Sometimes functions flatten out and other times functions increase or decrease without bound. There are basically three cases.
Case 1: Degree of Numerator is Less than Degree of Denominator
The first case is the function flattens out to 0 as x gets infinitely large or infinitely small. This happens when the degree of the numerator is less than the degree of the denominator. The degree is determined by the greatest exponent of x.
\(\ f(x)=\frac{2 x^{8}+3 x^{2}+100}{x^{9}-12}\)
One way to reason through why this makes sense is because when x is a ridiculously large number then most parts of the function hardly make any impact. The 100 for example is nothing in comparison and neither is the 3x2. The two important terms to compare are x8 and x9. The 2 isn’t even important now because if x is even just a million than the x9 will be a million times bigger than the x8 and the 2 hardly matters again. Essentially, when x gets big enough, this function acts like \(\ 1 \over 2\) which has a horizontal asymptote of 0.
Case 2: Degree of Numerator is Equal to the Degree of Denominator
If the degree of the numerator is equal to the degree of the denominator, the horizontal asymptote is equal to the ratio of the leading coefficients.
\(\ f(x)=\frac{6 x^{4}-3 x^{3}+12 x^{2}-9}{3 x^{4}+144 x-0.001}\)
Notice how the degree of both the numerator and the denominator is 4. This means that the horizontal asymptote is \(\ y=\frac{6}{3}=2\). One way to reason through why this makes sense is because when x gets to be a very large number all the smaller powers will not really make much of an impact. The biggest contributors are only the biggest powers. Then the value of the numerator will be about twice that of the denominator. As x gets even bigger, then the function will get even closer to 2.
Case 3: Degree of Numerator is Greater than the Degree of Denominator
If the degree of the numerator is greater than the degree of the denominator, there does not exist a horizontal asymptote. You must determine if the function increases or decreases without bound in both the left and right directions.
Watch the following video, focusing on the parts about horizontal asymptotes.
Examples
Earlier, you were asked if functions are allowed to touch their horizontal asymptotes.
Solution
Functions may touch and pass through horizontal asymptotes without limit. This is a difference between vertical and horizontal asymptotes. In calculus, there are rigorous proofs to show that functions like the one in Example C do become arbitrarily close to the asymptote.
Identify the vertical and horizontal asymptotes of the following rational function.
\(\ f(x)=\frac{(x-2)(4 x+3)(x-4)}{(x-1)(4 x+3)(x-6)}\)
Solution
There is factor that cancels that is neither a horizontal or vertical asymptote. The vertical asymptotes occur at x=1 and x=6. To obtain the horizontal asymptote you could methodically multiply out each binomial, however since most of those terms do not matter, it is more efficient to first determine the relative powers of the numerator and the denominator. In this case they both happen to be 3. Next determine the coefficient of the cubic terms only. The numerator will have 4x3 and the denominator will have 4x3 and so the horizontal asymptote will occur at \(\ y=\frac{4}{4}=1\).
Describe the right hand end behavior of the following function.
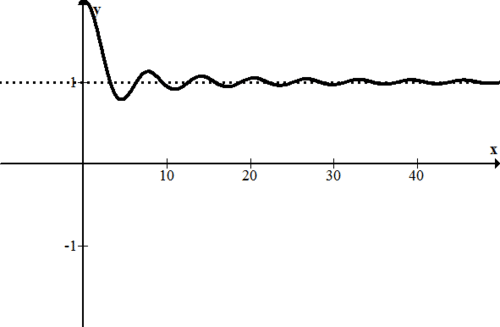 [Figure2]
[Figure2]Solution
Notice how quickly this dampening wave function settles down. There seems to be an obvious horizontal axis on the right at y=1
Identify the horizontal asymptotes of the following function.
\(\ f(x)=\frac{(x-3)(x+2)}{|(x-5)| \cdot(x-1)}\)
Solution
Add text hereFirst notice the absolute value surrounding one of the terms in the denominator. The degrees of both the numerator and the denominator will be 2 which means that the horizontal asymptote will occur at a number. As x gets infinitely large, the function is approximately:
\(\ f(x)=\frac{x^{2}}{x^{2}}\)
So the horizontal asymptote is y=−1 as x gets infinitely large.
On the other hand, as x gets infinitely small the function is approximately:
\(\ f(x)=\frac{x^{2}}{-x^{2}}\)
So the horizontal asymptote is y=−1 as x gets infinitely small.
In this case, you cannot blindly use the leading coefficient rule because the absolute value changes the sign.
Identify the horizontal asymptotes if they exist for the following 3 functions.
- \(\ f(x)=\frac{3 x^{6}-72 x}{x^{6}+999}\)
- \(\ h(x)=\frac{a x^{4}+b x^{3}+c x^{2}+d x+e}{f x^{4}+g x^{3}+h x^{2}}\)
- \(\ g(x)=\frac{f(x)}{h(x)}\)
Solution
- The degrees of the numerator and the denominatro are equal so the horizontal asymptote isy=3.
- The degrees of the numerator and the denominator are equal again so the horizontal asymptote is \(\ y=\frac{a}{f}\)
- As x gets infinitely large, \(\ g(x)=\frac{f(x)}{h(x)}=\frac{\frac{3 x^{6}-72 x}{x^{6}+999}}{\frac{a x^{4}+b x^{3}+c x^{2}+d x+e}{f x^{4}+g x^{3}+h x^{2}}} \approx \frac{3}{\frac{a}{f}}=\frac{3 f}{a}\)
When you study calculus, you will learn the rigorous techniques that enable you to feel more confident about results like this.
Review
Identify the horizontal asymptotes, if they exist, for the following functions.
- \(\ f(x)=\frac{5 x^{4}-2 x}{x^{4}+32}\)
- \(\ g(x)=\frac{3 x^{4}-2 x^{6}}{-x^{4}+2}\)
- \(\ h(x)=\frac{3 x^{4}-5 x}{8 x^{3}+3 x^{4}}\)
- \(\ j(x)=\frac{2 x^{3}-15 x}{-x^{4}+3}\)
- \(\ k(x)=\frac{2 x^{5}-3 x}{5 x^{2}+3 x^{4}+2 x-7 x^{5}}\)
- \(\ f(x)=\frac{a x^{14}+b x^{23}+c x^{12}+d x+e}{f x^{24}+g x^{23}+h x^{21}}\)
- \(\ g(x)=\frac{(x-1)(x+4)}{|(x-2)| \cdot(x-1)}\)
- Write a function that fits the following criteria:
- Vertical asymptotes at x=1 and x=4
- Zeroes at 3 and 5
- Hole when x=6
- Horizontal asymptote at \(\ y=\frac{2}{3}\)
- Write a function that fits the following criteria:
- Vertical asymptotes at x=−2 and x=2
- Zeroes at 1 and 5
- Hole when x=3
- Horizontal asymptote at y=1
- Write a function that fits the following criteria:
- Vertical asymptotes at x=0 and x=3
- Zeroes at 1 and 2
- Hole when x=8
- Horizontal asymptote at y=2
- Write a function that fits the following criteria:
- Vertical asymptotes at 2 and 6
- Zero at 5
- Hole when x=4
- Horizontal asymptote at y=0
- Write a function that fits the following criteria:
- Vertical asymptote at 4
- Zeroes at 0 and 3
- Hole at when x=5
- No horizontal asymptotes
Identify the vertical and horizontal asymptotes of the following rational functions.
- \(\ f(x)=\frac{(x-5)(2 x+1)(x-3)}{(x-3)(4 x+5)(x-6)}\)
- \(\ g(x)=\frac{x(x-1)(x+3)(x-5)}{3 x(x-1)(4 x+3)}\)
- \(\ h(x)=\frac{(x-2)(x+3)(x-6)}{(x-4)(x+3)^{2}(x+2)}\)
Vocabulary
| Term | Definition |
|---|---|
| End behavior | End behavior is a description of the trend of a function as input values become very large or very small, represented as the 'ends' of a graphed function. |
| Hole | A hole exists on the graph of a rational function at any input value that causes both the numerator and denominator of the function to be equal to zero. |
| Horizontal Asymptote | A horizontal asymptote is a horizontal line that indicates where a function flattens out as the independent variable gets very large or very small. A function may touch or pass through a horizontal asymptote. |
| Rational Function | A rational function is any function that can be written as the ratio of two polynomial functions. |
| Vertical Asymptote | A vertical asymptote is a vertical line marking a specific value toward which the graph of a function may approach, but will never reach. |
| Zero | The zeros of a function f(x) are the values of x that cause f(x) to be equal to zero. |
| Zeroes | The zeroes of a function f(x) are the values of x that cause f(x) to be equal to zero. |
| Zeros | The zeros of a function f(x) are the values of x that cause f(x) to be equal to zero. |
Image Attributions
- [Figure 1]
Credit: CK-12 Foundation
License: CC BY-SA - [Figure 2]
Credit: CK-12 Foundation
License: CC BY-SA

