3.4.3: Solving Logarithmic Equations

Last updated
Save as PDF

Page ID: 14378

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Solving Logarithmic Equations

This section addresses how to solve different types of logarithmic equations. It explores how to condense expanded equations and how to convert logarithmic equations into exponential ones. In addition, the section demonstrates how to check the solutions to logarithmic equations to be sure they are correct and not extraneous.

Warm-Up

Solutions to equations can be understood graphically as the location where two graphs intersect. Use the interactive below to visualize the solutions to logarithmic equations. Later in this section you will learn how to find these solutions algebraically.

*Interactive

Work it Out 1

Here is a logarithmic equation: log₂(x+3)=6.

How many processes can be used to solve this equation?
What are the different processes? What is the value of x?
Can these processes be applied to solving any logarithmic equation? If not, why might one process be applicable for some logarithmic equations and not others?
How do you check to make sure your answer is correct?

Discussion

Recall that a logarithmic equation is the inverse of an exponential equation. For example, if log_b(x+y)=z, then you can apply the inverse property b^log_bx=x to cancel out the log. Therefore, the equation log_b(x+y)=z can be rewritten as b^z=x+y. How can you apply this property to solve the equation in this problem?

This video provides a brief overview of the process for solving logarithmic equations.

Example 1

Solve the following logarithmic equation using two different processes, and check your answer to make sure your solution is not extraneous.

\(\ \log _{2}(x+5)=9\)

Solution

There are two different ways to solve this equation. The first is to use the definition of a logarithm.

\(\ \begin{aligned}
\log _{2}(x+5) &=9 \\
2^{9} &=x+5 \\
512 &=x+5 \\
507 &=x
\end{aligned}\)

The second way to solve this equation is to put everything into the exponent of 2, and then use the inverse property.

\(\ \begin{aligned}
2^{\log _{2}(x+5)} &=2^{9} \\
x+5 &=512 \\
x &=507
\end{aligned}\)

To check, plug in 507 for x.

\(\ \log _{2}(507+5)=9 \rightarrow \log _{2} 512=9\)

Work it Out 2

Calista was asked to solve the following logarithmic equation: \(\ \log 5 x+\log (x-1)=2\) Her work is shown below.

For each step, describe in writing what she is doing and why she is doing it. In other words, narrate the process she is using to solve the equation.
What solutions would she obtain by using this process?
Step 1: log5x+log(x−1)=2

Step 2: log[5x(x−1)]=2

Step 3: log(5x²−5x)=2

Step 4: \(\ 10^{\log \left(5 x^{2}-5 x\right)}=10^{2}\)

Step 5: 5x²−5x=100

Step 6: 5x²−5x−100=0

Step 7: x²−x−20=0

Step 8: (x−5)(x+4)=0

Discussion

In Step 1, Calista wrote the equation which she likely noticed includes several terms. In Step 2 she condenses the equation. Why did she do this? What did she do to condense the equation? In Step 4 she's changed the equation into an exponential one. Why did she feel this was necessary to do? How did she go from Step 3 to Step 4?

CK-12 INTERACTIVE

The following interactive will provide you with additional practice exploring the process for solving logarithmic equations.

Example 2

Start with the equation from above: log5x + log(x−1) = 2. Find the two solutions that Calista would have calculated, and check both answers.

Solution

The two solutions to this problem are x=5 and x=−4. Now check to confirm these solutions are correct by substituting them back into the original equation.

\(\ \begin{aligned}
\log 5(5)+\log (5-1) &=2 & & \log 5(-4)+\log ((-4)-1)=2 \\
\log 25+\log 4 &=2 & & \log (-20)+\log (-5)=2 \\
\log 100 &=2 & &
\end{aligned}\)

In the step on the right, log(−20) + log(−5) = 2, both logs have negative values, and you cannot take the log of a negative number. Therefore -4 is considered an extraneous solution, or in other words, it is not a solution. 5 is the only solution.

Work it Out 3

Terrance was working to solve this equation: log10x²− logx = 3, but isn't sure how to get started. What would be the first step he would take, and why? What solution would he eventually find?

Discussion

Recall the subtraction/division property for logs. When subtracting one logarithmic term from another with the same bases, you can pull out the log function and combine the remaining part of each term into a fraction or division problem. Perform this step for Terrance, and then solve the rest of the equation.

CK-12 INTERACTIVE

The following interactive will help you explore the relationship between exponential, radical, and logarithmic equations.

Work it Out 4

Start with the equation y=log₂(x)

Graph the equation.
What is the value of x when y=4? Show this on the graph and solve algebraically.
What are the domain and range of this function? What is the vertical asymptote?

Discussion

You should use a graphing utility to visualize the curve of this equation. Predict what would look different about a graph as the base got larger, and then check your prediction by graphing additional equations.

Example 3

Given the equation y=log₅x+2

a. Graph the equation.

b. Determine the value of x when y=2.

c. What is the domain and range of the function?

d. Determine the equation for the vertical asymptote.

Solution

a. 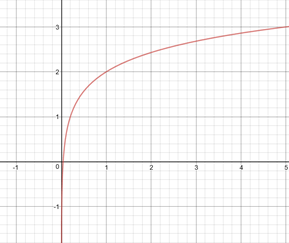f-d_41a98ca10deed9ca6d1c9b17b52a57966504df656a20797e701e506f+IMAGE_THUMB_POSTCARD_TINY+IMAGE_THUMB_POSTCARD_TINY.png

b. When y=2 then x=1.

c. Domain: (0,∞); Range: (−∞,∞).

d. Vertical Asymptote: x=0 .

Review

Use properties of logarithms and a calculator to solve the following equations for x. Round answers to three decimal places and check for extraneous solutions.

\(\ \log_2x=15\)
\(\ \log_{12}x=2.5\)
\(\ \log_9(x−5)=2\)
\(\ \log_7(2x+3)=3\)
\(\ 4\log_33x−\log_3x=5\)
\(\ \log(x+5)+\log x=\log14\)
\(\ 3\log_3(x−5)=3\)
\(\ \frac{2}{3} \log _{3} x=2\)
\(\ 5 \log \frac{x}{2}-3 \log \frac{1}{x}=\log 8\)
\(\ 2 \log _{6} x+1=\log _{6}(5 x+4)\)
\(\ 2 \log _{\frac{1}{2}} x+2=\log _{\frac{1}{2}}(x+3)\)
\(\ 3 \log _{\frac{2}{3}} x-\log _{\frac{2}{3}} 27=\log _{\frac{2}{3}} 8\)

Work it Out

Found a content error?
Tell us