6.3.2: Equations of Hyperbolas Centered at the Origins

Last updated
Save as PDF

Page ID: 14759

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Writing the Equation of a Hyperbola, Centered at the Origin

You are asked to solve a riddle. You are given the following pieces of information to help you.

I am a hyperbola centered at the origin.
My vertex is (0, −2).
One of my foci is (0, −3).

What is my equation?

The Equation of a Hyperbola

In this concept, we are going to work backwards and find the equation of hyperbolas, given certain pieces of information. For this entire concept, the hyperbola will be centered at the origin.

Let's find the equation of the hyperbola, centered at the origin, with a vertex of (−4, 0) and focus of (−6, 0).

Because the vertex and focus are on the \(\ x \text {-axis }\), we know that the transverse axis is horizontal.

Therefore, the equation will be \(\ \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\). From the vertex, we know that \(\ a=4\) and \(\ c=6\). Let’s solve for \(\ b^{2}\) using \(\ c^{2}=a^{2}+b^{2}\).

\(\ \begin{array}{l}
6^{2}=4^{2}+b^{2} \\
36=16+b^{2} \rightarrow b^{2}=20
\end{array}\)

The equation of the hyperbola is \(\ \frac{x^{2}}{16}-\frac{y^{2}}{20}=1\).

Now, let's find the equation of the hyperbola, centered at the origin, with an asymptote of \(\ y=\frac{2}{3} x\) and vertex of \(\ (0,12)\).

We know that \(\ a=12\), making the transverse axis is vertical and the general equation of the asymptote \(\ y=\frac{a}{b} x\). Therefore, \(\ \frac{2}{3}=\frac{12}{b}\), making \(\ b=18\). Therefore, the equation of the hyperbola is \(\ \frac{y^{2}}{144}-\frac{x^{2}}{324}=1\).

In this problem, we showed that the slope of the asymptote can be reduced to something that is not always \(\ \frac{a}{b}\), but \(\ c\left(\frac{m}{n}\right)=\frac{a}{b}\), where \(\ c\) is some constant that we can reduce the fraction by.

Finally, let's find the equations of two hyperbolas with an asymptote of \(\ y=-\frac{5}{9} x\).

This asymptote can be for either a vertical or horizontal hyperbola. \(\ -\frac{5}{9}\) can also be a reduced fraction of \(\ \frac{a}{b}\), like in the previous problem. For example, the asymptote \(\ y=-\frac{10}{18} x\) reduces to \(\ y=-\frac{5}{9} x\).

If the hyperbola is horizontal, then the equation of the asymptote is \(\ y=-\frac{b}{a} x\) and that would make \(\ a=9\) and \(\ b=5\) and the equation would be \(\ \frac{x^{2}}{81}-\frac{y^{2}}{25}=1\). If the equation is vertical, then the asymptote is \(\ y=-\frac{a}{b} x\) and \(\ a=5\) and \(\ b=9\). The equation would be \(\ \frac{y^{2}}{25}-\frac{x^{2}}{81}=1\). If the slope is reduced from a larger fraction, we could also have \(\ \frac{x^{2}}{324}-\frac{y^{2}}{100}=1\) or \(\ \frac{y^{2}}{100}-\frac{x^{2}}{324}=1\) as a possible answer.

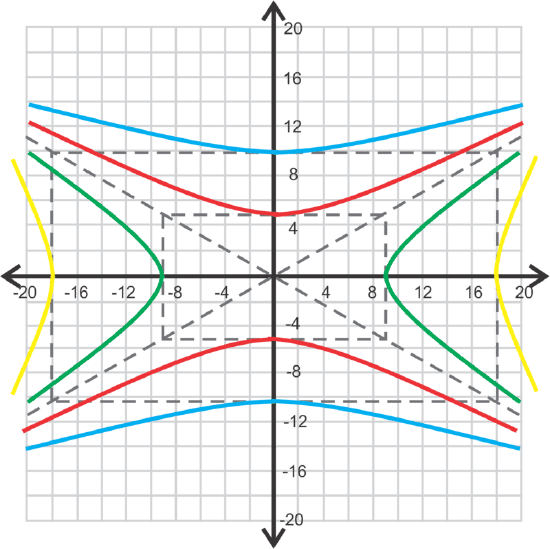
f-d_b2872a6f99a25ed745302d03cd9d6358b7ef838b3936f14be81d7f1e+IMAGE_TINY+IMAGE_TINY.png

There are infinitely many hyperbolic equations with this asymptote.

Examples

Example 1

Earlier, you were asked to find the equation of the parabola given the riddle.

Solution

Because the vertex and focus are on the \(\ y \text {-axis }\), we know that the transverse axis is vertical.

Therefore, the equation will be \(\ \frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\).

From the vertex and the focus, we know that \(\ a=2\) and \(\ c=3\). Let’s solve for \(\ b^{2}\) using \(\ c^{2}=a^{2}+b^{2}\).

\(\ \begin{aligned}
3^{2} &=2^{2}+b^{2} \\
9 &=4+b^{2} \rightarrow b^{2}=5
\end{aligned}\)

Therefore, the equation of the hyperbola will be \(\ \frac{y^{2}}{4}-\frac{x^{2}}{5}=1\).

Find the equation of the following hyperbolas, centered at the origin, with the given information.

Example 2

vertex: (0, 2)

focus: (0, 5)

Solution

The vertex is on the y-axis, so this is a vertical hyperbola with \(\ a=2\). \(\ c=5\), so we need to find \(\ b^{2}\).

\(\ \begin{array}{l}
c^{2}&=a^{2}+b^{2} \\
25&=4+b^{2} \rightarrow b^{2}=21
\end{array}\)

The equation of the hyperbola is \(\ \frac{y^{2}}{4}-\frac{x^{2}}{21}=1\).

Example 3

asymptote: \(\ y=x\)

vertex: \(\ (4,0)\)

Solution

Rewriting the slope of \(\ y=x\), we get \(\ y=\frac{1}{1} x\). So, we know that \(\ a\) and \(\ b\) are in a ratio of 1:1.

Because the vertex is \(\ (4,0)\), we know that \(\ a=4\) and that the hyperbola is horizontal. Because \(\ a\) and \(\ b\) are in a ratio of 1:1, \(\ b\) has to equal 4 as well. The equation of the hyperbola is \(\ \frac{x^{2}}{16}-\frac{y^{2}}{16}=1\).

Example 4

Find the equations of two hyperbolas, centered at the origin, with different \(\ a\) and \(\ b\) values and an asymptote of \(\ y=\frac{3}{4} x\).

Solution

One possibility is that \(\ b=3\) and \(\ a=4\) making the equation \(\ \frac{x^{2}}{16}-\frac{y^{2}}{9}=1\). A second possibility could be that \(\ a\) and \(\ b\) are a multiply of the ratio 4:3. So, \(\ a=8\) and \(\ b=6\), making the equation \(\ \frac{x^{2}}{64}-\frac{y^{2}}{36}=1\).

Review

Find the equation of the hyperbola, centered at the origin, given the information below.

vertex: \(\ (−2,0)\), focus: \(\ (−5,0)\)
vertex: \(\ (4,0)\), focus: \(\ (7,0)\)
\(\ b=8\), focus: \(\ (−15,0)\)
vertex: \(\ (−6,0)\), asymptote: \(\ y=\frac{4}{3} x\)
\(\ b=6\), focus: \(\ (0,11)\)
vertex: \(\ (0,5)\), asymptote: \(\ y=x\)
asymptote: \(\ y=-\frac{1}{2} x\), vertex: \(\ (6,0)\)
asymptote: \(\ y=3x\), \(\ b=9\), vertical transverse axis
vertex: \(\ (0,8)\), focus: \(\ (0,6 \sqrt{2})\)
Find the equation of two hyperbolas such that they have the same \(\ a\) and \(\ b\) values, the equation of an asymptote is \(\ y=\frac{4}{5} x\), and centered at the origin.
Find the equation of two hyperbolas such that they have different \(\ a\) and \(\ b\) values, both horizontal, the equation of an asymptote is \(\ y=-\frac{2}{3} x\), and centered at the origin.
Find the equation of two hyperbolas such that they have different \(\ a\) and \(\ b\) values, both vertical, the equation of an asymptote is \(\ y=6x\), and centered at the origin.
Find the equation of two hyperbolas such that they have the same \(\ a\) and \(\ b\) values, the equation of an asymptote is \(\ y=-\frac{10}{7} x\), and centered at the origin.