6.4.2: Circles Not Centered at the Origin

Circles Centered at (h, k)

You draw a circle that is centered at (−2, −2). You measure the diameter of the circle to be 18 units. Does the point (4, 5) lie on the circle?

---

Circles Centered at (h,k)

When a circle is centered at the origin, the equation is \(\ x^{2}+y^{2}=r^{2}\). If we rewrite this equation, using the center, it would look like \(\ (x-0)^{2}+(y-0)^{2}=r^{2}\). Extending this idea to any point as the center, we would have \(\ (x-h)^{2}+(y-k)^{2}=r^{2}\), where \(\ (h,k)\) is the center.

Let's find the center and radius of \(\ (x+1)^{2}+(y-3)^{2}=16\) and graph.

Using the general equation above, the center would be \(\ (-1,3)\) and the radius is \(\ \sqrt{16}\) or 4. To graph, plot the center and then go out 4 units up, down, to the left, and to the right.

Now, let's find the equation of the circle with center (2,4) and radius 5.

Plug in the center and radius to the equation and simplify.

\(\ \begin{array}{l}
(x-2)^{2}+(y-4)^{2}=5^{2} \\
(x-2)^{2}+(y-4)^{2}=25
\end{array}\)

Finally, let's find the equation of the circle with center (6, −1) and (5, 2) is on the circle.

In this problem, we are not given the radius. To find the radius, we must use the distance formula, \(\ d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\).

\(\ \begin{aligned}
r &=\sqrt{(5-6)^{2}+(2-(-1))^{2}} \\
&=\sqrt{(-1)^{2}+3^{2}} \\
&=\sqrt{1+9} \\
&=\sqrt{10}
\end{aligned}\)

Therefore, the equation of this circle is \(\ (x-6)^{2}+(y-(-1))^{2}=(\sqrt{10})^{2}\) or \(\ (x-6)^{2}+(y+1)^{2}=10\).

---

Examples

Example 1

Earlier, you were asked to determine if the point (4, 5) lies on the circle.

Solution

In this lesson, you learned the equation of a circle that is centered somewhere other than the origin is \(\ (x-h)^{2}+(y-k)^{2}=r^{2}\), where \(\ (h,k) \)is the center.

We are given that the center is \(\ (−2,−2)\), so \(\ h=−2\) and \(\ k=−2\). We are also given the diameter of the circle, but we need the radius. Recall that the radius is half the diameter, so \(\ r=\frac{18}{2}=9\).

If we plug these values into the equation for the circle, we get:

\(\ \begin{aligned}
(x-h)^{2}+(y-k)^{2} &=r^{2} \\
(x-(-2))^{2}+(y-(-2))^{2} &=9^{2} \\
(x+2)^{2}+(y+2)^{2} &=81
\end{aligned}\)

Now to find if the point \(\ (4, 5)\) lies on the circle we substitute 4 for x and 5 for y and see if the equation holds true.

\(\ \begin{aligned}
(x+2)^{2}+(y+2)^{2} &=81 \\
(4+2)^{2}+(5+2)^{2} & \stackrel{?}{=} 81 \\
6^{2}+7^{2} & \stackrel{?}{=} 81 \\
85 & \neq 81
\end{aligned}\)

Therefore, the point does not lie on the circle.

Example 2

Graph \(\ (x+4)^{2}+(y+3)^{2}=25\) and find the center and radius.

Solution

The center is (−4, −3) and the radius is 5.

Example 3

Find the equation of the circle with center (−8, 3) and (2, −5) is on the circle.

Solution

Use the distance formula to find the radius.

\(\ \begin{aligned}
r &=\sqrt{(2-(-8))^{2}+(-5-3)^{2}} \\
&=\sqrt{10^{2}+(-8)^{2}} \\
&=\sqrt{100+64} \\
&=\sqrt{164}
\end{aligned}\)

The equation of this circle is \(\ (x+8)^{2}+(y-3)^{2}=164\)

Example 4

The endpoints of a diameter of a circle are (−3, 1) and (9, 6). Find the equation.

Solution

In this example, we are not given the center or radius. We can find the length of the diameter using the distance formula and then divide it by 2.

\(\ \begin{aligned}
&d=\sqrt{(9-(-3))^{2}+(6-1)^{2}}\\
&=\sqrt{12^{2}+5^{2}} \quad \quad \quad \quad \quad \text { The radius is } 13 \div 2=\frac{13}{2}\\
&\begin{array}{l}
=\sqrt{144+25} \\
=\sqrt{169}=13
\end{array}
\end{aligned}\)

Now, we need to find the center. Use the midpoint formula with the endpoints.

\(\ \begin{aligned}
c &=\left(\frac{-3+9}{2}, \frac{1+6}{2}\right) \\
&=\left(3, \frac{7}{2}\right)
\end{aligned}\)

Therefore, the equation is \(\ (x-3)^{2}+\left(y-\frac{7}{2}\right)^{2}=\frac{169}{4}\).

---

Review

For questions 1-4, match the equation with the graph.

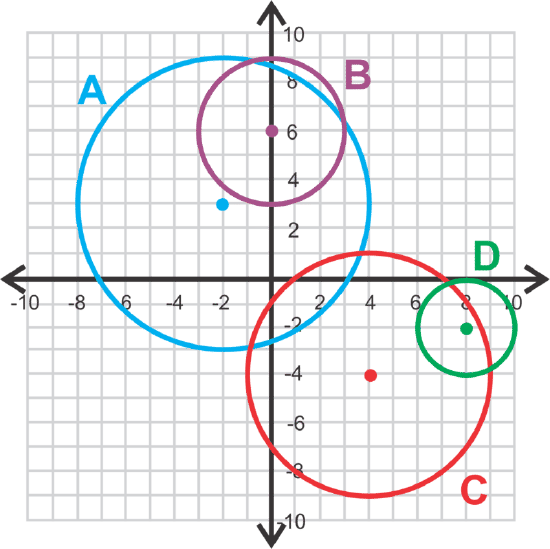
1. \(\ (x-8)^{2}+(y+2)^{2}=4\)
2. \(\ x^{2}+(y-6)^{2}=9\)
3. \(\ (x+2)^{2}+(y-3)^{2}=36\)
4. \(\ (x-4)^{2}+(y+4)^{2}=25\)

Graph the following circles. Find the center and radius.

5. \(\ (x-2)^{2}+(y-5)^{2}=16\)
6. \(\ (x+4)^{2}+(y+3)^{2}=18\)
7. \(\ (x+7)^{2}+(y-1)^{2}=8\)

Find the equation of the circle, given the information below.

8. center: \(\ (−3,−3)\) radius: \(\ 7\)
9. center: \(\ (−7,6)\) radius: \(\ \sqrt{15}\)
10. center: \(\ (8,−1)\) point on circle: \(\ (0,14)\)
11. center: \(\ (−2,−5)\) point on circle: \(\ (3,2)\)
12. diameter endpoints: \(\ (−4,1)\) and \(\ (6,3)\)
13. diameter endpoints: \(\ (5,−8)\) and \(\ (11,2)\)
14. Is \(\ (−9,12)\) on the circle \(\ (x+5)^{2}+(y-6)^{2}=54\)? How do you know?
15. Challenge Use the following steps to find the equation of the tangent line to the circle with center \(\ (3,−4)\) and the point of tangency \(\ (−1,8)\).
    1. Find the slope of the radius from the center to \(\ (−1,8)\).
    2. Find the perpendicular slope to (a). This is the slope of the tangent line.
    3. Use the slope from (b) and the given point to find the equation of the tangent line.
16. Extension Rewrite the equation of the circle, \(\ x^{2}+y^{2}+4 x-8 y+11=0\) in standard form by completing the square for both the x and y terms. Then, find the center and radius.

---

Answers for Review Problems

To see the Review answers, open this PDF file and look for section 10.4.

---

Vocabulary

Term	Definition
Standard Form	The standard form of a circle is \(\ (x-h)^{2}+(y-k)^{2}=r^{2}\), where \(\ (h,k)\) is the center and \(\ r\) is the radius.

---

Image Attributions

1. [Figure 1]
   Credit: Tony Webster
   Source: https://commons.wikimedia.org/wiki/File%3ALas_Vegas_High_Roller_(20216869960).jpg