6.5.4: Solving Systems of Lines, Quadratics, and Conics

Last updated
Save as PDF

Page ID: 14771

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Solving Systems of Lines, Quadratics, and Conics

You are given the ellipse \(\ \frac{x^{2}}{4}+\frac{y^{2}}{9}=1\) and the line \(\ y=\frac{3}{2} x+3\). You want to determine at which point(s), if any, the two equations intersect without graphing. Does the line intersect the ellipse? If so, at which point(s) does it do so?

Systems of Lines, Quadratics and Conics

Previously, we solved a system involving two lines or three planes, by using graphing, substitution, and linear combinations. In this concept, we will add circles, parabolas, and ellipses to systems of equations. Because both x and y can be squared in these equations, there will often be more than one answer.

Let's estimate the solutions for the system of equations below.

f-d_771037c9651f8761bce5cf471f04219cc0f4ad015f8a903616a18d08+IMAGE_TINY+IMAGE_TINY.png

These two ellipses intersect in four places. They look to be the following points:

(0, 7), (4.7, 5.5), (4.9, 4.3), and (−1, 2.9)

Keep in mind these are only estimates. In the next problem, we will show how to find the exact answers.

Now, let's solve

\(\ \begin{array}{l}
x^{2}+y^{2}=25 \\
3 x+2 y=6
\end{array}\)

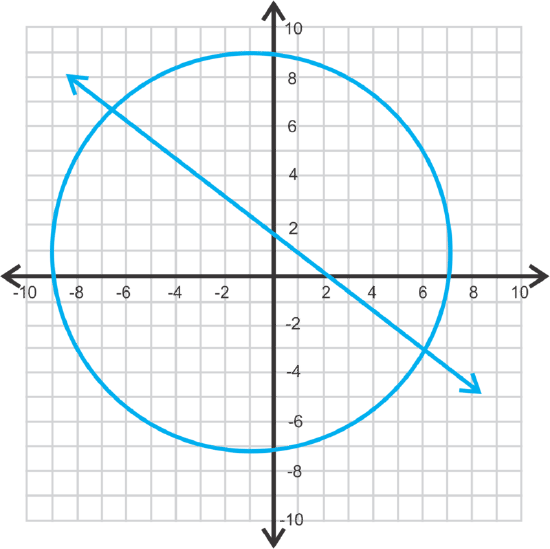
Let’s solve this system by graphing. The first equation is a circle, centered at the origin, with a radius of 5. The second equation is a line. In slope intercept form, it is \(\ y=-\frac{3}{2} x+3\).

f-d_e40ea0e331f32d5b74dd42f12b505121322a00fdaaef4acac30dee70+IMAGE_TINY+IMAGE_TINY.png

Next, let’s estimate where the line and circle intersect. In the second quadrant, it looks like (−1.2, 4.8) and in the fourth quadrant it looks like (4, −3). These are our estimated answers.

To find the exact value of these points of intersection, we need to use substitution. Substitute in the linear equation in for y into the circle equation and solve for x.

\(\ \begin{aligned}
x^{2}+\left(-\frac{3}{2} x+3\right)^{2} &=25 \\
x^{2}+\frac{9}{4} x^{2}-9 x+9 &=25 \\
\frac{13}{4} x^{2}-9 x-16 &=0 \\
13 x^{2}-36 x-64 &=0
\end{aligned}\)

Use the Quadratic Formula:

\(\ \begin{aligned}
x &=\frac{36 \pm \sqrt{36^{2}-4(13)(-64)}}{2(13)} \\
&=\frac{36 \pm \sqrt{4624}}{26} \\
&=\frac{36 \pm 68}{26}
\end{aligned}\)

The solutions, for x, are \(\ \frac{36+68}{26}=4\) and \(\ \frac{36-68}{26}=-1 \frac{3}{13}\). Plug these into either equation to solve for y.

\(\ y=-\frac{3}{2}(4)+3=-3\) and \(\ y=-\frac{3}{2}\left(-\frac{16}{13}\right)+3=4 \frac{11}{13}\)

The points are (4, −3) and \(\ \left(-1 \frac{3}{13}, 4 \frac{11}{13}\right)\).

The technique used in this problem is how it is recommended you approach each problem. First, graph the system so that you have an idea of how many solutions there are and where they are located. Then, use substitution to solve for the exact answers.

Finally, let's solve

\(\ \begin{array}{l}
\frac{x^{2}}{16}+\frac{y^{2}}{9}=1 \\
y^{2}=-\frac{4}{3}(x-6)
\end{array}\)

Graphing the two equations, we have four points of intersection below. The second equation is solved for \(\ y^{2}\), so substitute that into the first equation.

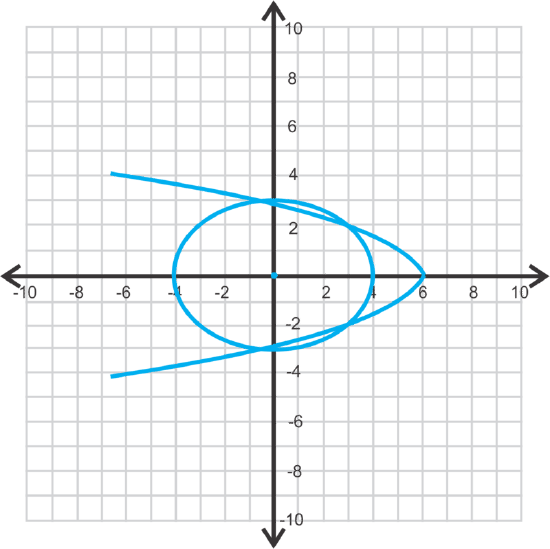
f-d_2ccc0468a2b0e068a4e99fa451a6252804a42d6b99f7930bd4a6bf68+IMAGE_TINY+IMAGE_TINY.png

\(\ \begin{aligned}
\frac{x^{2}}{16}-\frac{4(x-6)}{3 \cdot 9} &=1 \\
\frac{x^{2}}{16}-\frac{4 x-24}{27} &=1 \\
27 x^{2}-16(4 x-24) &=432 \\
27 x^{2}-64 x-48 &=0
\end{aligned}\)

Now, use the Quadratic Formula to solve for x.

\(\ \begin{aligned}
x &=\frac{64 \pm \sqrt{(-64)^{2}-4(27)(-48)}}{2(27)} \\
&=\frac{64 \pm \sqrt{9280}}{54} \\
&=\frac{32 \pm 4 \sqrt{145}}{27}
\end{aligned}\)

Plugging these into the calculator we get \(\ x=\frac{32+4 \sqrt{145}}{27} \approx 2.97\) and \(\ x=\frac{32-4 \sqrt{145}}{27} \approx-0.6\). Looking at the graph, we know that there will be two different y-values for each x-value to give four points of intersection. Using the estimations, solve for y. You can choose either equation.

\(\ \begin{array}{rlrl}
y^{2} & =-\frac{4}{3}(2.97-6) & & y^{2}&=-\frac{4}{3}(-0.6-6) \\
y^{2} & =4.04 & \text { and } & y^{2} & =8.8 \\
y & =\pm 2.01 && y & =\pm 2.97
\end{array}\)

The points are (2.97, 2.01), (2.97, −2.01), (−0.6, 2.97), and (−0.6, −2.97).

Examples

Example 1

Earlier, you were asked to determine if the line \(\ y=\frac{3}{2} x+3\) intersects the ellipse \(\ \frac{x^{2}}{4}+\frac{y^{2}}{9}=1\), and if so, at which point(s).

Solution

First, let's get rid of the fractions in the equation of the ellipse to make it easier to work with. To do so, we multiply by the LCD.

\(\ \begin{array}{r}
\frac{x^{2}}{4}+\frac{y^{2}}{9}=1 \\
36 \frac{x^{2}}{4}+36 \frac{y^{2}}{9}=36 \cdot 1 \\
9 x^{2}+4 y^{2}=36
\end{array}\)

Now we can substitute the equation of the line \(\ y=\frac{3}{2} x+3\) in for y and solve for x.

\(\ \begin{array}{r}
9 x^{2}+4\left(\frac{3}{2} x+3\right)^{2}=36 \\
9 x^{2}+4\left(\frac{9}{4} x^{2}+9 x+9\right)=36 \\
9 x^{2}+9 x^{2}+36 x+36=36 \\
18 x^{2}+36 x=0 \\
18 x(x+2)=0
\end{array}\)

So, \(\ x=0\) or \(\ x=−2\)

Finally we can substitute these x values into the equation of the line to find the corresponding y values.

\(\ \begin{array}{l}
y=\frac{3}{2}(0)+3=3 \\
y=\frac{3}{2}(-2)+3=0
\end{array}\)

Therefore, the line intersects the ellipse at points \(\ (0, 3)\) and \(\ (−2, 0)\).

Example 2

Estimate the solutions to the system below.

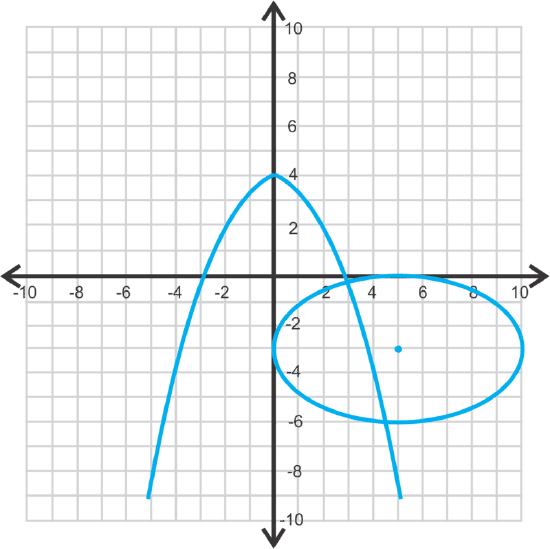
f-d_99e460286b4a8e2e7c2aadd946c322c7138aeb6981ee7370051dadbd+IMAGE_TINY+IMAGE_TINY.png

Solution

(3, −0.1) and (4.5, −6)

Find the solutions to the systems below.

Example 3

\(\ \begin{aligned}
x^{2}+(y-1)^{2} &=36 \\
x^{2} &=2(y+9)
\end{aligned}\)

Solution

This is a circle and a parabola that intersects in four places.

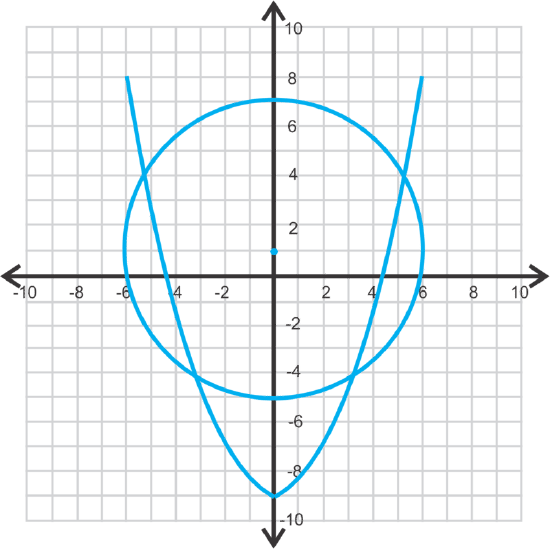
f-d_97e889a13b96b60777b750a5dbf49adb49696c64158a3d5eae2a31bc+IMAGE_TINY+IMAGE_TINY.png

Using substitution for \(\ x^{2}\), we have:

\(\ \begin{aligned}
2(y+9)+(y-1)^{2} &=36 \\
2 y+18+y^{2}-2 y+1 &=36 \\
y^{2} &=17 \\
y &=\pm \sqrt{17} \approx \pm 4.12
\end{aligned}\)

The corresponding x-values are:

\(\ \begin{aligned}
x^{2} &=2(4.12+9) & x^{2}&=2(-4.12+9) \\
x^{2} &=26.25 \quad\quad\quad\quad\text { and } & x^{2}&=9.76 \\
x &=\pm 5.12 & x&=\pm 3.12
\end{aligned}\)

The solutions are: (4.12, 5.12), (4.12, −5.12), (−4.12, 3.12) and (−4.12, −3.12).

Example 4

\(\ \begin{aligned}
x^{2} &=y+8 \\
4 x+5 y &=12
\end{aligned}\)

Solution

This is a line and a parabola that intersect in two points.

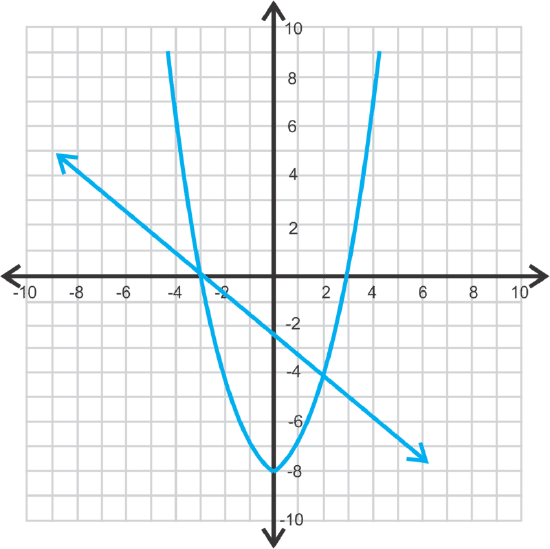
f-d_4a6f3ea2964e9189e7475b690ffd91080890611b89ffc9c7bdb0e569+IMAGE_TINY+IMAGE_TINY.png

Solve the first equation for y and substitute into the second.

\(\ \begin{aligned}
4 x+5\left(x^{2}-8\right) &=12 \\
4 x+5 x^{2}-40 &=12 \\
5 x^{2}+4 x-52 &=0 \\
x &=\frac{-4 \pm \sqrt{4^{2}-4(5)(-52)}}{2(5)} \\
x &=\frac{-4 \pm \sqrt{1056}}{10} \approx 3.65,2.85
\end{aligned}\)

Using the first equation, \(\ y=3.65^{2}-8=5.32\) and \(\ y=2.85^{2}-8=0.12\). The points are \(\ (3.65,5.32)\) and \(\ (2.85,0.12)\).

Review

Estimate the solutions for each system of equations below.

Solve each system of equations below.

\(\ \begin{aligned}
5 x^{2}+3 y &=17 \\
x-y &=1
\end{aligned}\)
\(\ \begin{array}{c}
x^{2}+y^{2}=7.5 \\
x+2 y=6
\end{array}\)
\(\ \begin{aligned}
x^{2} &=y+4 \\
\frac{x^{2}}{4}+(y+2)^{2} &=1
\end{aligned}\)
\(\ \begin{aligned}
(x-1)^{2}+(y-3)^{2} &=25 \\
x^{2} &=-2(y-10)
\end{aligned}\)
\(\ \begin{array}{l}
x^{2}+y^{2}=16 \\
4 x-3 y=18
\end{array}\)
\(\ \begin{aligned}
(x+4)^{2}+(y+1)^{2} &=36 \\
\frac{(x+1)^{2}}{4}+\frac{(y-2)^{2}}{25} &=1
\end{aligned}\)
How many different ways can a circle and a parabola intersect? Draw each possibility.
How many different ways can a circle and an ellipse intersect? Draw each possibility.
Create a system of two circles with no solution. What would the graph look like?
Challenge Find the solutions for the system
\(\ \begin{aligned}
x^{2}+y^{2} &=r^{2} \\
y &=m x
\end{aligned}\)

Leave your answers in terms of \(\ m\) and \(\ r\).

Challenge Determine if the system of three equations below have one common solution.
\(\ \begin{aligned}
x^{2}+3 y^{2} &=16 \\
3 x^{2}+y^{2} &=16 \\
y &=x
\end{aligned}\)