1.1: Pythagorean Theorem
- Page ID
- 4143
Discover, geometrically prove, and apply the Pythagorean Theorem.
Lengths of Triangle Sides Using the Pythagorean Theorem
You've just signed up to be an architect's assistant in a new office downtown. You're asked to draw a scale model of a sculpture for a business plaza. The sculpture has a large triangular piece where one of the angles between the sides is ninety degrees. This type of triangle is called a ‘‘right triangle’’. The architect you're working for comes into the room and tells you that the sides of the triangle that form the right angle are 9 feet and 12 feet. Can you tell how long the third side is?
Finding the Length of Triangle Sides Using Pythagorean Theorem
From Geometry, recall that the Pythagorean Theorem is \(a^2+b^2=c^2\) where \(a\) and \(b\) are the legs of a right triangle and \(c\) is the hypotenuse. Also, the side opposite the angle is lower case and the angle is upper case. For example, angle \(A\) is opposite side \(a\).
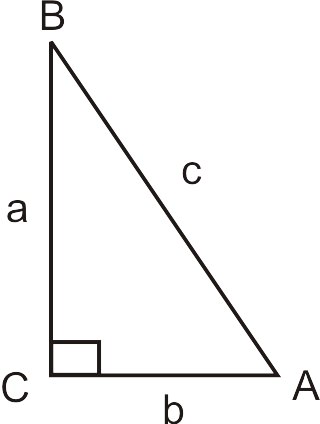
The Pythagorean Theorem is used to solve for the sides of a right triangle.
Using the Pythagorean Theorem
1.
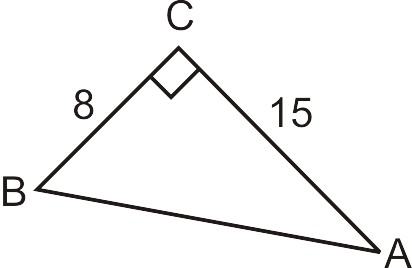
\(a=8\), \(b=15\), we need to find the hypotenuse.
\(\begin{aligned} 8^2+15^2&=c^2 \\ 64+225&=c^2 \\ 289&=c^2 \\ 17&=c \end{aligned}\)
Notice, we do not include -17 as a solution because a negative number cannot be a side of a triangle.
2.
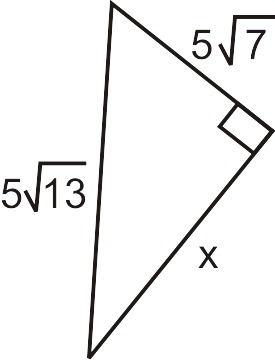
Use the Pythagorean Theorem to find the missing leg.
\(\begin{aligned} (5\sqrt{7})^2+x^2&=(5\sqrt{13})^2 \\ 25\cdot 7+x^2&=25\cdot 13 \\ 175+x^2&=325 \\ x^2&=150 \\ x&=5\sqrt{6}\end{aligned}\)
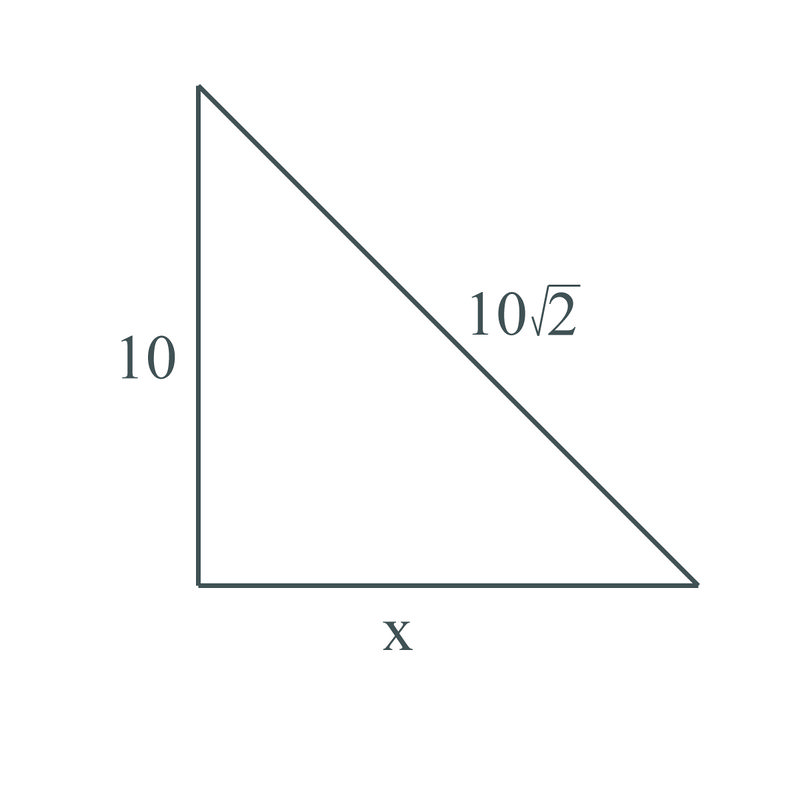
3. Use the Pythagorean Theorem to find the missing leg in the triangle above.
\(\begin{aligned} 10^2+x^2&=(10\sqrt{2})^2 \\ 100+x^2&=100\cdot 2 \\ 100+x^2&=100 \\ x^2&=100 \\ x&=10 \end{aligned}\)
Earlier, you were given a problem asking you to draw a scale model of a sculpture for a business plaza.
With your knowledge of the Pythagorean Theorem, you can see that the triangle has sides with lengths 9 feet and 12 feet. You work to find the hypotenuse:
Solution
\(\begin{aligned} a^2+b^2&=c^2 \\ 9^2+12^2&=c^2 \\ 81+144&=c^2 \\ 225&=c^2 \\ (\sqrt{225})&=15=c \end{aligned}\)
With the knowledge that the length of the third side of the triangle is 15 feet, you are able to construct your scale model with ease.
Use the Pythagorean Theorem to find the missing side of the following triangle:
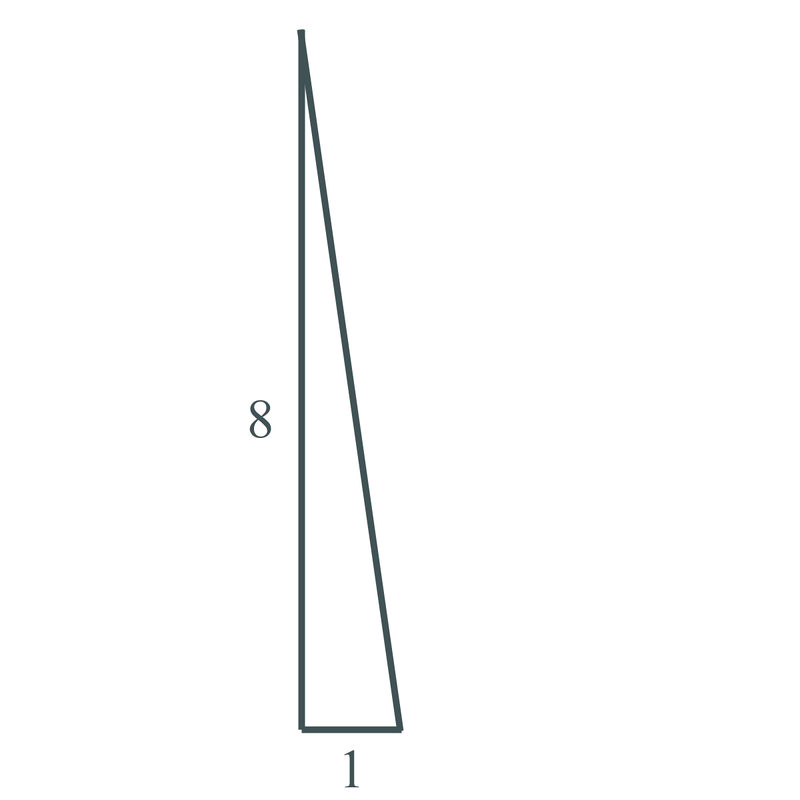
Solution
\(a=1\), \(b=8\), we need to find the hypotenuse.
\(\begin{aligned} 1^2+8^2&=c^2 \\ 1+64&=c^2 \\ 65&=c^2 \\ \sqrt{65}&=c\end{aligned}\)
Use the Pythagorean Theorem to find the missing side of the following triangle:
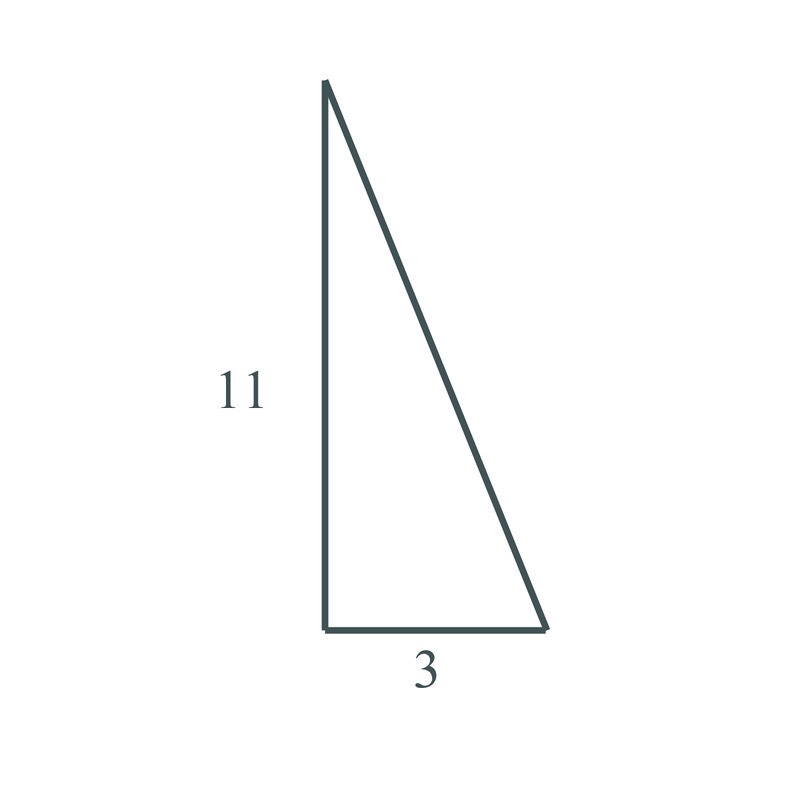
Solution
\(a=3\), \(b=11\), we need to find the length of side c, the hypotenuse.
\(\begin{aligned} 3^2+11^2&=c^2 \\ 9+121&=c^2 \\ 130&=c^2 \\ \sqrt{130}&=c\end{aligned}\)
Find the missing side of the right triangle below. Leave the answer in simplest radical form.
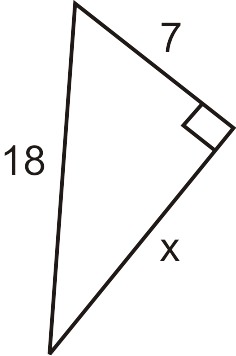
Solution
\(a=7\), \(c=18\), we need to find the length of side b.
\(\begin{aligned}7^2+b^2=18^2 \\ 49+b^2=18^2 \\ 324−49=b^2 \\ 275=b^2 \\ \sqrt{275}=b \end{aligned}\)
Review
Find the missing sides of the right triangles. Leave answers in simplest radical form.
- If the legs of a right triangle are 3 and 4, then the hypotenuse is _____________.
- If the legs of a right triangle are 6 and 8, then the hypotenuse is _____________.
- If the legs of a right triangle are 5 and 12, then the hypotenuse is _____________.
- If the sides of a square are length 6, then the diagonal is _____________.
- If the sides of a square are 9, then the diagonal is _____________.
- If the sides of a square are \(x\), then the diagonal is _____________.
- If the legs of a right triangle are 3 and 7, then the hypotenuse is _____________.
- If the legs of a right triangle are \(2\sqrt{5}\) and 6, then the hypotenuse is _____________.
- If one leg of a right triangle is 4 and the hypotenuse is 8, then the other leg is _____________.
- If one leg of a right triangle is 10 and the hypotenuse is 15, then the other leg is _____________.
- If one leg of a right triangle is \(4\sqrt{7}\) and the hypotenuse is \(10\sqrt{6}\), then the other leg is _____________.
- If the legs of a right triangle are x and y, then the hypotenuse is ____________.
Pythagorean Theorem Proof
Use the picture below to answer the following questions.

- Find the area of the square in the picture with sides (a+b).
- Find the sum of the areas of the square with sides c and the right triangles with legs a and b.
- Explain why the areas found in the previous two problems should be the same value. Then, set the expressions equal to each other and simplify to get the Pythagorean Theorem.
Review (Answers)
To see the Review answers, open this PDF file and look for section 1.1.
Vocabulary
| Term | Definition |
|---|---|
| Pythagorean Theorem | The Pythagorean Theorem is a mathematical relationship between the sides of a right triangle, given by \(a^2+b^2=c^2\), where a and b are legs of the triangle and \(c\) is the hypotenuse of the triangle. |

