2.3.10: Exact Values for Inverse Sine, Cosine, and Tangent

Last updated
Save as PDF

Page ID: 14466

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Find all angles on unit circle matching exact trig ratios

You are working with a triangular brace in shop class. The brace is a right triangle, and the length of one side of the bracket is \(\sqrt{3}\approx 1.732\) and it is connected to the other side at a right angle. The length of the other side is 1. You need to find the angle that the third piece makes with the first piece, labelled below as "C":

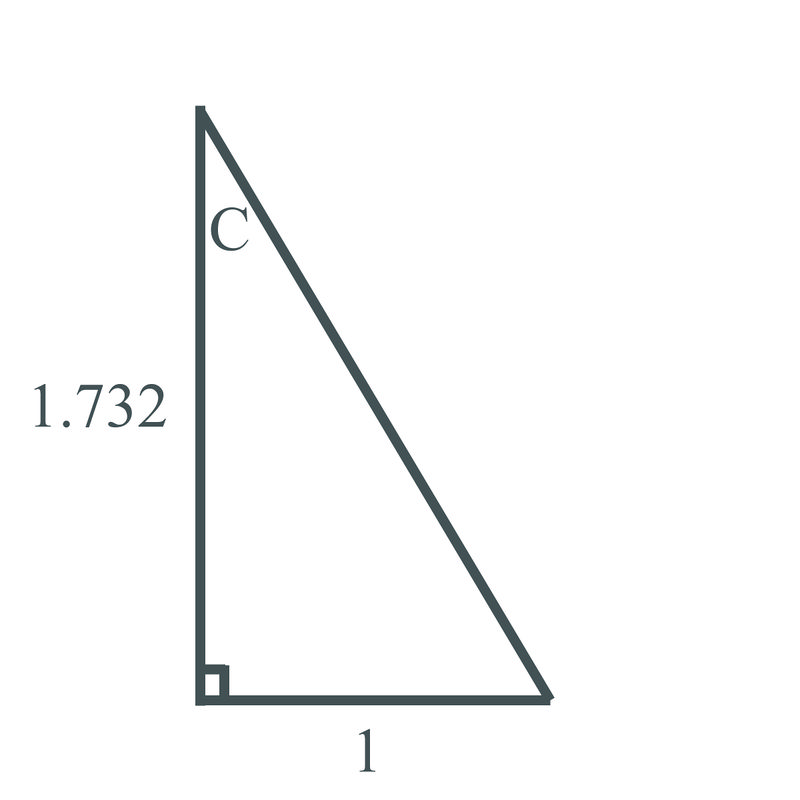
f-d_acae0d7fee4f7c9a78d3e265620b1d464df685bc8ee315d2c90a8c66+IMAGE_TINY+IMAGE_TINY.jpg — Figure \(\PageIndex{1}\)

Can you find the angle between the legs of the brace?

By the time you finish reading this lesson, you'll be able to answer this question.

Inverse of Sine, Cosine and Tangent

Inverse trig functions can be useful in a variety of math problems for finding angles that you need to know. In many cases, such as angles involving multiples of \(30^{\circ}\), \(60^{\circ} \) and \(90^{\circ}\), the values of trig functions are often memorized, since they are used so often.

Recall the unit circle and the critical values. With the inverse trigonometric functions, you can find the angle value (in either radians or degrees) when given the ratio and function. Make sure that you find all solutions within the given interval.

Let's take a look at a few example problems.

1. Find the exact value of the expression without a calculator, in \([0,2\pi )\).

\(\sin^{-1}\left(−\dfrac{\sqrt{3}}{2}\right)\)

This is a value from the special right triangles and the unit circle.

Recall that \(−\dfrac{\sqrt{3}}{2}\) is from the 30−60−90 triangle. The reference angle for sin and \(\dfrac{\sqrt{3}}{2}\) would be \(60^{\circ}\). Because this is sine and it is negative, it must be in the third or fourth quadrant. The answer is either \(\dfrac{4\pi }{3}\) or \(\dfrac{5\pi }{3}\).

2. Find the exact value of the expression without a calculator, in \([0,2\pi )\).

\(\cos^{-1}\left(−\dfrac{\sqrt{2}}{2}\right)\)

This is a value from the special right triangles and the unit circle.

\(−\dfrac{\sqrt{2}}{2}\) is from an isosceles right triangle. The reference angle is then \(45^{\circ}\). Because this is cosine and negative, the angle must be in either the second or third quadrant. The answer is either \(\dfrac{3\pi }{4}\) or \(\dfrac{5\pi }{4}\).

3. Find the exact value of the expression without a calculator, in \([0, 2\pi )\).

\(\tan^{-1}\sqrt{3}\)

This is a value from the special right triangles and the unit circle.

\(\sqrt{3}\) is also from a 30−60−90 triangle. Tangent is \(\sqrt{3}\) for the reference angle \(60^{\circ}\). Tangent is positive in the first and third quadrants, so the answer would be \(\dfrac{\pi}{3}\) or \(\dfrac{4\pi}{3}\).

Example \(\PageIndex{1}\)

Earlier, you were asked to find the angle between the legs of the brace.

Solution

Using your knowledge of the values of trig functions for angles, you can work backward to find the angle that the brace makes:

\(\begin{aligned} \tan C &=\dfrac{1}{\sqrt{3}} \\ \tan^{-1} C &=\tan^{-1}\dfrac{1}{\sqrt{3}} \\ C&=60^{\circ} \end{aligned}\)

Example \(\PageIndex{2}\)

Find the exact value of the inverse function of \(\cos^{-1}(0)\), without a calculator in \([0,2\pi)\)

Solution

\(\dfrac{\pi }{2}, \dfrac{3\pi}{2}\)

Example \(\PageIndex{3}\)

Find the exact value of the inverse function of \(\tan^{-1}(−\sqrt{3})\), without a calculator in \([0, 2\pi )\)

Solution

\(\dfrac{2\pi }{3}, \dfrac{5\pi }{3}\)

Example \(\PageIndex{4}\)

Find the exact value of the inverse function of \(\sin^{-1}(−12)\), without a calculator in \([0, 2\pi )\)

Solution

\(\dfrac{11\pi}{6}, \dfrac{7\pi}{6}\)

Review

Find the exact value of each expression without a calculator, in \([0, 2\pi )\).

\(\sin^{-1}\left(\dfrac{\sqrt{2}}{2}\right)\)
\(\cos^{-1}\left(\dfrac{1}{2}\right)\)
\(\sin^{-1}(1)\)
\(\cos^{-1}\left(−\dfrac{\sqrt{3}}{2}\right)\)
\(\tan^{-1}\left(−\dfrac{\sqrt{3}}{3}\right)\)
\(\tan^{-1}(−1)\)
\(\sin^{-1}\left(\dfrac{\sqrt{3}}{2}\right)\)
\(\cos^{-1}\left(\dfrac{\sqrt{2}}{2}\right)\)
\(\csc ^{-1}(\sqrt{2})\)
\(\sec ^{-1}(−2)\)
\(\cot ^{-1}\left(\dfrac{\sqrt{3}}3\right)\)
\(\sec ^{-1}\left(\dfrac{2\sqrt{3}}{2}\right)\)
\(\csc ^{-1}\left(−\dfrac{2\sqrt{3}}{2}\right)\)
\(\cot ^{-1}(−\sqrt{3})\)
\(\cot ^{-1}(−1)\)

Review (Answers)

To see the Review answers, open this PDF file and look for section 4.2.

Vocabulary

Term	Definition
Trigonometric Inverse	A trigonometric inverse is a function that undoes a trigonometric function to give the original argument of the function. It can also be used to find a missing angle of a triangle from the ratio of two sides of the triangle.

Additional Resources

Video: Examples: Determine Trig Function Values Using Reference Triangles

Practice: Exact Values for Inverse Sine, Cosine, and Tangent