2.2.1: The Pythagorean Theorem and Trigonometry
- Page ID
- 14306
Using trigonometric functions or the pythagorean theorem based on given information.
A 40-foot-tall tree casts a shadow of 80 feet. What is the angle of elevation from the end of the shadow to the top of the tree with respect to the ground?
Application Problems
When solving word problems, it is important to understand the terminology used to describe angles. In trigonometric problems, the terms angle of elevation and angle of depression are commonly used. Both of these angles are always measured from a horizontal line as shown in the diagrams below.

Let's solve the following problems.
- An airplane approaching an airport spots the runway at an angle of depression of \(25^{\circ}\). If the airplane is 15,000 ft above the ground, how far (ground distance) is the plane from the runway? Give your answer to the nearest 100 ft.
Make a diagram to illustrate the situation described and then use a trigonometric ratio to solve. Keep in mind that an angle of depression is down from a horizontal line of sight-in this case a horizontal line from the pilot of the plane parallel to the ground.
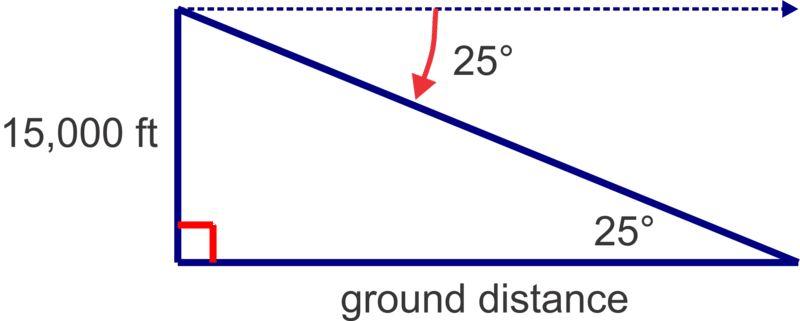
Note that the angle of depression and the alternate interior angle will be congruent, so the angle in the triangle is also \(25^{\circ}\).
From the picture, we can see that we should use the tangent ratio to find the ground distance.
\(\begin{aligned} \tan 25^{\circ}&=\dfrac{15000}{d} \\ d&=\dfrac{15000}{\tan 25^{\circ}} \approx 32,200 \text{ ft}\end{aligned}\)
- Rachel spots a bird in a tree at an angle of elevation of \(30^{\circ}\). If Rachel is 20 ft from the base of the tree, how high up in the tree is the bird? Give your answer to the nearest tenth of a foot.
Make a diagram to illustrate the situation. Keep in mind that there will be a right triangle and that the right angle is formed by the ground and the trunk of the tree.
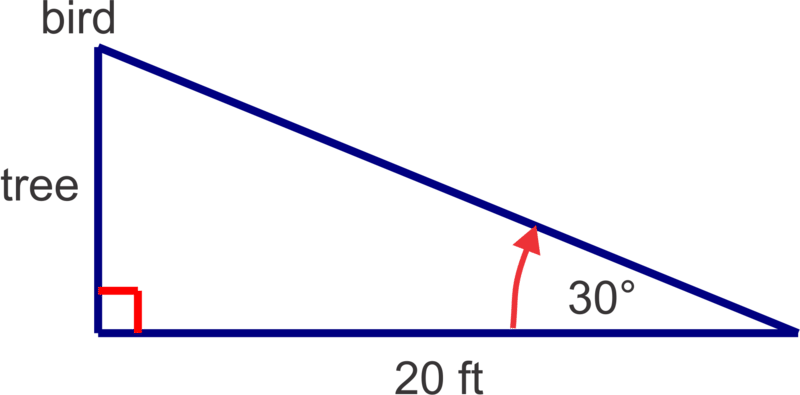
Here we can use the tangent ratio to solve for the height of the bird
\(\begin{aligned} tan 30^{\circ}&=\dfrac{h}{20} \\ h&=20 \tan 30^{\circ}\approx 11.5 \text{ ft}\end{aligned}\)
- A 12 ft ladder is leaning against a house and reaches 10 ft up the side of the house. To the nearest degree, what angle does the ladder make with the ground?
In this problem, we will need to find an angle. By making a sketch of the triangle we can see which inverse trigonometric ratio to use.
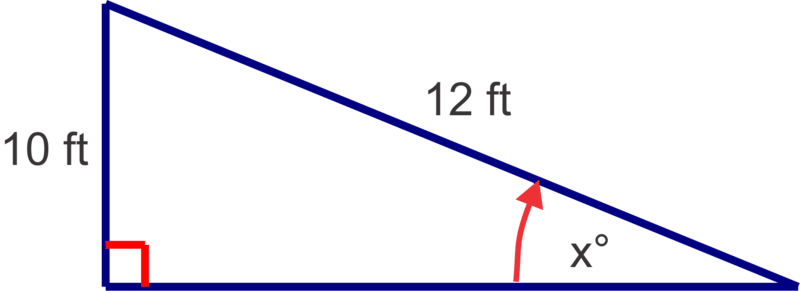
\(\begin{aligned} sin x^{\circ} &=\dfrac{10}{12}\\ sin^{−1}(\dfrac{10}{12}) &\approx 56^{\circ} \end{aligned}\)
Earlier, you were asked to find the angle of elevation from the end of the shadow to the top of the tree with respect to the ground.
Solution
If you draw this situation, you will see that we are dealing with a right triangle. The side opposite the angle of elevation is 40. The side adjacent to the angle is 80. Therefore, we can use the tangent to find the angle of elevation.
\(\begin{aligned} \tan x^{\circ}&=\dfrac{40}{80}=\dfrac{1}{2}\\ tan^{−1}(\dfrac{1}{2})&=\approx 26.57^{\circ} \end{aligned}\)
A ramp makes a \(20^{\circ}\) angle with the ground. If door the ramp leads to is 2 ft above the ground, how long is the ramp? Give your answer to the nearest tenth of a foot.
Solution
\(\begin{aligned} \sin 20^{\circ}&=\dfrac{2}{x} \\ x&=\dfrac{2}{sin20^{\circ}}\approx 5.8 \text{ ft} \end{aligned}\)
Charlie lets out 90 ft of kite string. If the angle of elevation of the string is 70^{\circ}, approximately how high is the kite? Give your answer to the nearest foot.
Solution
\(\begin{aligned} \sin 70^{\circ}&=\dfrac{x}{90} \\ x&=90 \sin 70^{\circ}\approx 85 \text{ ft}\end{aligned}\)
A ship’s sonar spots a wreckage at an angle of depression of 32^{\circ}. If the depth of the ocean is about 250 ft, how far is the wreckage (measured along the surface of the water) from the ship, to the nearest foot.
Solution
\(\begin{aligned} \tan 32^{\circ}&=\dfrac{250}{x} \\ x&=\dfrac{250}{\tan 32^{\circ}} \approx 400 \text{ ft} \end{aligned}\)
Review
Use the Pythagorean Theorem and/or trigonometry to solve the following word problems.
- A square has sides of length 8 inches. To the nearest tenth of an inch, what is the length of its diagonal?
- Layne spots a sailboat from her fifth floor balcony, about 25 m above the beach, at an angle of depression of \(3^{\circ}\). To the nearest meter, how far out is the boat?
- A zip line takes passengers on a 200 m ride from high up in the trees to a ground level platform. If the angle of elevation of the zip line is \(10^{\circ}\), how high above ground is the tree top start platform? Give your answer to the nearest meter.
- The angle of depression from the top of an apartment building to the base of a fountain in a nearby park is \(57^{\circ}\). If the building is 150 ft tall, how far away, to the nearest foot, is the fountain?
- A playground slide platform is 6 ft above ground. If the slide is 8 ft long and the end of the slide is 1 ft above ground, what angle does the slide make with the ground? Give your answer to the nearest degree.
- Benjamin spots a tree directly across the river from where he is standing. He then walks 27 ft upstream and determines that the angle between his previous position and the tree on the other side of the river is \(73^{\circ}\). How wide, to the nearest foot, is the river?
- A rectangle has sides of length 6 in and 10 in. To the nearest degree, what angle does the diagonal make with the longer side?
- Tommy is flying his kite one afternoon and notices that he has let out the entire 130 ft of string. The angle his string makes with the ground is \(48^{\circ}\). How high, to the nearest foot, is his kite at this time?
- A tree struck by lightning in a storm breaks and falls over to form a triangle with the ground. The tip of the tree makes a \(18^{\circ}\) angle with the ground 21 ft from the base of the tree. What was the height of the tree to the nearest foot?
- Upon descent an airplane is 19,000 ft above the ground. The air traffic control tower is 190 ft tall. It is determined that the angle of elevation from the top of the tower to the plane is \(15^{\circ}\). To the nearest mile, find the ground distance from the airplane to the tower.
- Why will the sine and cosine ratios always be less than 1?
Answers for Review Problems
To see the Review answers, open this PDF file and look for section 13.4.
Additional Resources
Video: Solving Right Triangles - Overview
Practice: The Pythagorean Theorem and Trigonometry

