2.2.6: Inverse Trig Functions using Algebra
- Page ID
- 14348
"Undo" a function by switching \(x\) and \(y\) values and solving for \(y\).
If you were given a function, such as \(f(x)=\dfrac{2x}{x+7}\), can you tell if the function has an inverse? Is there a way that you could find its inverse through algebraic manipulation?
Finding the Inverse of a Function
An "inverse" is something that undoes a function, giving back the original argument. For example, a function such as \(y=\dfrac{1}{3}x\) has an inverse function of \(y=3x\), since any value placed into the first function will be returned as what it originally was if it is input into the second function. In this case, it is easy to see that to "undo" multiplication by \(\dfrac{1}{3}\), you should multiply by 3. However, in many cases it may not be easy to infer by examination what the inverse of a function is.
To start, let's examine what is required for a function to have an inverse. It is important to remember that each function has an inverse relation and that this inverse relation is a function only if the original function is one-to-one. A function is one-to-one when its graph passes both the vertical and the horizontal line test. This means that every vertical and horizontal line will intersect the graph in exactly one place.
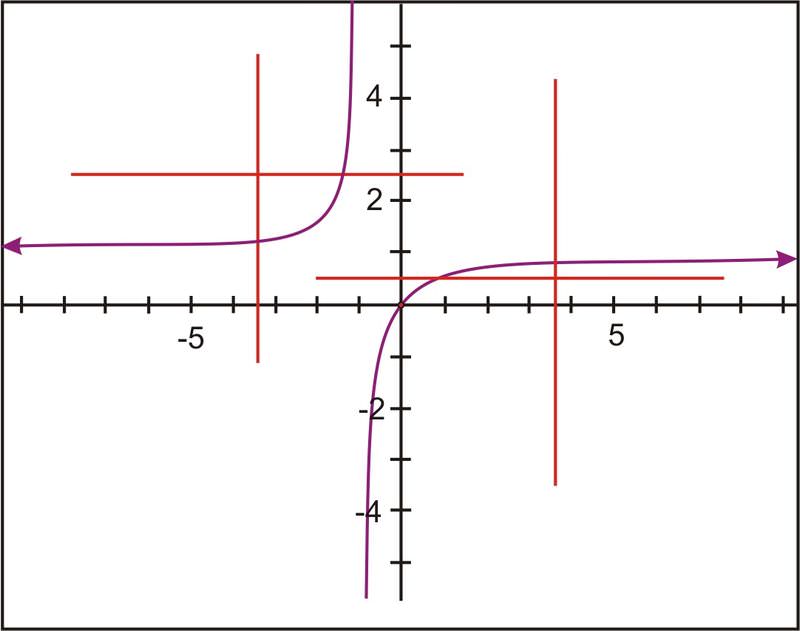
This is the graph of \(f(x)=\dfrac{x}{x+1}\). The graph suggests that \(f\) is one-to-one because it passes both the vertical and the horizontal line tests. To find the inverse of \(f\), switch the \(x\) and \(y\) and solve for \(y\).
First, switch \(x\) and \(y\).
\(x=\dfrac{y}{y+1}\)
Next, multiply both sides by \((y+1)\).
\(\begin{aligned} (y+1)x&=\dfrac{y}{y+1}(y+1) \\ x(y+1)&=y \end{aligned}\)
Then, apply the distributive property and put all the y terms on one side so you can pull out the y.
\(\begin{aligned} xy+x=y \\ xy−y=−x \\ y(x−1)=−x \end{aligned}\)
Divide by \((x−1)\) to get \(y\) by itself.
\(y=\dfrac{−x}{x−1}\)
Finally, multiply the right side by \(\dfrac{−1}{−1}\).
\(y=\dfrac{x}{1−x}\)
Therefore the inverse of f is \(f^{−1}(x)=\dfrac{x}{1−x}\).
The symbol \(f^{−1}\) is read “f inverse” and is not the reciprocal of f.
Finding the Inverse of a Function
1. Find the inverse of \(f(x)=\dfrac{1}{x−5}\) algebraically.
To find the inverse algebraically, switch \(f(x)\) to \(y\) and then switch \(x\) and \(y\).
\(\begin{aligned} y&=1x−5\\ x&=1y−5 \\ x(y−5)&=1 \\ xy−5x&=1 \\ xy&=5x+1 \\ y&=\dfrac{5x+1}{x}\end{aligned}\)
2. Find the inverse of \(f(x)=5 \sin^{−1} (\dfrac{2}{x−3})\)
\(\begin{aligned}
f(x) &=5 \sin ^{-1}\left(\dfrac{2}{x-3}\right) \\
x &=5 \sin ^{-1}\left(\dfrac{2}{y-3}\right) \\
\dfrac{x}{5} &=\sin ^{-1}\left(\dfrac{2}{y-3}\right) \\
\sin \dfrac{x}{5} &=\left(\dfrac{2}{y-3}\right) \\
(y-3) \sin \dfrac{x}{5} &=2 \\
(y-3) &=\dfrac{2}{\sin \dfrac{x}{5}} \\
y &=\dfrac{2}{\sin \dfrac{x}{5}}+3
\end{aligned}\)
3. Find the inverse of the trigonometric function \(f(x)=4 \tan^{−1} (3x+4)\)
\(\begin{aligned}
x &=4 \tan ^{-1}(3 y+4) \\
\dfrac{x}{4} &=\tan ^{-1}(3 y+4) \\
\tan \dfrac{x}{4} &=3 y+4 \\
\tan \dfrac{x}{4}-4 &=3 y \\
\dfrac{\tan \dfrac{x}{4}-4}{3} &=y \\
f^{-1}(x) &=\dfrac{\tan \dfrac{x}{4}-4}{3}
\end{aligned}\)
Earlier, you were asked to find the inverse of a function.
Solution
Since the original function is:
\(f(x)=y=\dfrac{2x}{x+7}\)
You can first switch all of the "\(x\)" and "\(y\)" values:
\(x=\dfrac{2y}{y+7}\)
You can then rearrange the equation and isolate "y":
\(\begin{array}{r}
x(y+7)=2 y \\
x y+7 x=2 y \\
x y-2 y=-7 x \\
y(x-2)=-7 x \\
y=\dfrac{-7 x}{x-2}
\end{array}\)
The inverse function is written as \(f^{−1}(x)=\dfrac{−7x}{x−2}\)
Find the inverse of \(f(x)=2x^3−5\)
Solution
\(\begin{aligned}
f(x) &=2 x^{3}-5 \\
y &=2 x^{3}-5 \\
x &=2 y^{3}-5 \\
x+5 &=2 y^{3} \\
\dfrac{x+5}{2} &=y^{3} \\
\sqrt[3]{\dfrac{x+5}{2}} &=y
\end{aligned}\)
Find the inverse of \(y=\dfrac{1}{3} \tan^{−1}(\dfrac{3}{4} x−5)\)
Solution
\(\begin{aligned}
y &=\dfrac{1}{3} \tan ^{-1}\left(\dfrac{3}{4} x-5\right) \\
x &=\dfrac{1}{3} \tan ^{-1}\left(\dfrac{3}{4} y-5\right) \\
3 x &=\tan ^{-1}\left(\dfrac{3}{4} y-5\right) \\
\tan (3 x) &=\dfrac{3}{4} y-5 \\
\tan (3 x)+5 &=\dfrac{3}{4} y \\
\dfrac{4(\tan (3 x)+5)}{3} &=y
\end{aligned}\)
Find the inverse of \(g(x)=2 \sin(x−1)+4\)
Solution
\(\begin{aligned}
g(x) &=2 \sin (x-1)+4 \\
y &=2 \sin (x-1)+4 \\
x &=2 \sin (y-1)+4 \\
x-4 &=2 \sin (y-1) \\
\dfrac{x-4}{2} &=\sin (y-1) \\
1+\sin ^{-1}\left(\dfrac{x-4}{2}\right) &=y
\end{aligned}\)
Review
Find the inverse of each function.
- \(f(x)=3x+5\)
- \(g(x)=0.2x−7\)
- \(h(x)=0.1x^2\)
- \(k(x)=5x+6\)
- \(f(x)=\sqrt{x−4}\)
- \(g(x)=(x)^{\dfrac{1}{3}}+1\)
- \(h(x)=(x+1)^3\)
- \(k(x)=\dfrac{x^2}{3}\)
- \(f(x)=−2+4 \sin^{−1} (x+7)\)
- \(g(x)=1+3 \tan^{−1}(2x+1)\)
- \(h(x)=4 \cos^{−1}(3x)\)
- \(k(x)=−1 \tan^{−1} (6x)\)
- \(j(x)=5+2 \sin^{−1}(x+5)\)
- \(m(x)=−2 \tan (3x+1)\)
- \(p(x)=5−6 \sin(\dfrac{x}{2})\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 4.3.
Vocabulary
| Term | Definition |
|---|---|
| Horizontal Line Test | The horizontal line test says that if a horizontal line drawn anywhere through the graph of a function intersects the function in more than one location, then the function is not one-to-one and not invertible. |
| One to One Function | A function is one to one if its inverse is also a function. A one-to-one function passes both the horizontal and vertical line tests. |
| Vertical Line Test | The vertical line test says that if a vertical line drawn anywhere through the graph of a relation intersects the relation in more than one location, then the relation is not a function. |

