2.3.9: Trigonometric Functions of Angles Greater than 360 Degrees

Last updated
Save as PDF

Page ID: 14465

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Based on coterminal and reference angles.

While out at the local amusement park with friends, you take a ride on the Go Karts. You ride around a circular track in the carts three and a half times, and then stop at a "pit stop" to rest. While waiting for your Go Kart to get more fuel, you are talking with your friends about the ride. You know that one way of measuring how far something has gone around a circle (or the trig values associated with it) is to use angles. However, you've gone more than one complete circle around the track.

Is it still possible to find out what the values of sine and cosine are for the change in angle you've made?

Angles Greater Than 360°

Consider the angle \(390^{\circ}\). As you learned previously, you can think of this angle as a full 360 degree rotation, plus an additional 30 degrees. Therefore \(390^{\circ}\) is coterminal with \(30^{\circ}\). As you saw above with negative angles, this means that \(390^{\circ}\) has the same ordered pair as \(30^{\circ}\), and so it has the same trig values. For example,

\(\cos 390^{\circ}=\cos 30^{\circ}=\dfrac{\sqrt{3}}{2}\)

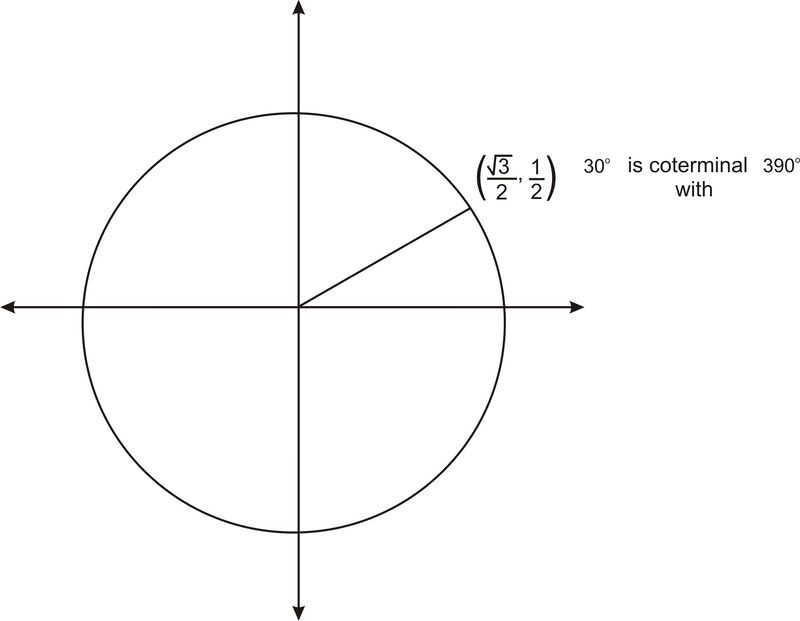
f-d_f9c84652e3661fa4ed33d2d13150ee7aadf408553ed0ce0a280c2a8a+IMAGE_TINY+IMAGE_TINY.jpg — Figure \(\PageIndex{1}\)

In general, if an angle whose measure is greater than

\(360^{\circ}\) has a reference angle of \(30^{\circ}\), \(45^{\circ}\), or \(60^{\circ}\), or if it is a quadrantal angle, we can find its ordered pair, and so we can find the values of any of the trig functions of the angle. Again, determine the reference angle first.

Let's look at some problems involving angles greater than \(360^{\circ}\).

Find the value of the following expressions:

1. \(\sin 420^{\circ}\)

\(\sin 420^{\circ}=\dfrac{\sqrt{3}}{2}\)

\(420^{\circ}\) is a full rotation of 360 degrees, plus an additional 60 degrees. Therefore the angle is coterminal with \(60^{\circ}\), and so it shares the same ordered pair, \(\left(\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right)\). The sine value is the \(y\)−coordinate.

2. \(\tan 840^{\circ}\)

\(\tan 840^{\circ}=−\sqrt{3}\)

\(840^{\circ}\) is two full rotations, or 720 degrees, plus an additional 120 degrees:

\(840=360+360+120\)

Therefore \(840^{\circ}\) is coterminal with \(120^{\circ}\), so the ordered pair is \(\left(−\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right)\). The tangent value can be found by the following:

\(\tan 840^{\circ}=\tan 120^{\circ}=\dfrac{y}{x}=\dfrac{\dfrac{\sqrt{3}}{2}}{−\dfrac{1}{2}}=\dfrac{\sqrt{3}}{2}\times −\dfrac{2}{1}=−\sqrt{3}\)

3. \(\cos 540^{\circ}\)

\(\cos 540^{\circ}=−1\)

\(540^{\circ}\) is a full rotation of 360 degrees, plus an additional 180 degrees. Therefore the angle is coterminal with \(180^{\circ}\), and the ordered pair is \((-1, 0)\). So the cosine value is -1.

Example \(\PageIndex{1}\)

Earlier, you were asked if it is still possible to find out what the values of sine and cosine are for the change in angle.

Solution

Since you've gone around the track 3.5 times, the total angle you've traveled is \(360^{\circ}\times 3.5=1260^{\circ}\). However, as you learned in this unit, this is equivalent to \(180^{\circ}\). So you can use that value in your computations:

\(\begin{aligned} \sin 1260^{\circ}&=\sin 180^{\circ}=0 \\ \cos 1260^{\circ}&=\cos 180^{\circ}=−1 \end{aligned}\)

Example \(\PageIndex{2}\)

Find the value of the expression: \(\sin 570^{\circ}\)

Solution

Since \(570^{\circ}\) has the same terminal side as \(210^{\circ}\), \(\sin 570^{\circ}=\sin 210^{\circ}=\dfrac{\dfrac{−1}{2}}{1}=\dfrac{−1}{2}\)

Example \(\PageIndex{3}\)

Find the value of the expression: \(\cos 675^{\circ}\)

Solution

Since \(675^{\circ}\) has the same terminal side as \(315^{\circ}\), \(\cos 675^{\circ}= \cos 315^{\circ}=\dfrac{\dfrac{\sqrt{2}}{2}}{1}=\dfrac{\sqrt{2}}{2}\)

Example \(\PageIndex{4}\)

Find the value of the expression: \(\sin 480^{\circ}\)

Solution

Since \(480^{\circ}\) has the same terminal side as \(120^{\circ}\), \(\sin 480^{\circ}=\sin 120^{\circ}=\dfrac{\dfrac{\sqrt{3}}{2}}{1}=\dfrac{\sqrt{3}}{2}\)

Review

Find the value of each expression.

\(\sin 405^{\circ}\)
\(\cos 810^{\circ}\)
\(\tan 630^{\circ}\)
\(\cot 900^{\circ}\)
\(csc 495^{\circ}\)
\(\sec 510^{\circ}\)
\(\cos 585^{\circ}\)
\(\sin 600^{\circ}\)
\(\cot 495^{\circ}\)
\(\tan 405^{\circ}\)
\(\cos 630^{\circ}\)
\(\sec 810^{\circ}\)
\(\csc 900^{\circ}\)
\(\tan 600^{\circ}\)
\(\sin 585^{\circ}\)
\(\tan 510^{\circ}\)
Explain how to evaluate a trigonometric function for an angle greater than \(360^{\circ}\).