3.3.4: Cosine Sum and Difference Formulas
- Page ID
- 4210
cosine of a sum or difference related to a set of cosine and sine functions.
While playing a board game with friends, you are using a spinner like this one:

When you tap the spinner with your hand, it rotates \(110^{\circ}\). However, at that moment, someone taps the game board and the spinner moves back a little to \(80^{\circ}\). One of your friends, who is a grade above you in math, starts talking to you about trig functions.
"Do you think you can calculate the cosine of the difference between those angles?" he asks.
"Hmm," you reply. "Sure. I think it's just \(\cos (110^{\circ} −80^{\circ} )=\cos 30^{\circ}\)."
Your friend smiles. "Are you sure?" he asks.
You realize you aren't sure at all. Can you solve this problem? Read this lesson, and by the end you'll be able to calculate the cosine of the difference of the angles.
Formulas for the Sum and Difference of cosines
When thinking about how to calculate values for trig functions, it is natural to consider what the value is for the trig function of a difference of two angles.
For example, is \(\cos 15^{\circ} =\cos (45^{\circ} −30^{\circ} )\)? Upon appearance, yes, it is. This section explores how to find an expression that would equal \(\cos (45^{\circ} −30^{\circ} )\). To simplify this, let the two given angles be \(a\) and \(b\) where \(0<b<a<2\pi\).
Begin with the unit circle and place the angles a and b in standard position as shown in Figure A. Point Pt1 lies on the terminal side of \(b\), so its coordinates are \((\cos b, \; \sin b)\) and Point Pt2 lies on the terminal side of a so its coordinates are \((\cos a,\sin a)\). Place the \(a−b\) in standard position, as shown in Figure B. The point A has coordinates \((1,0)\) and the Pt3 is on the terminal side of the angle \(a−b\), so its coordinates are \((\cos [a−b],\sin [a−b])\).
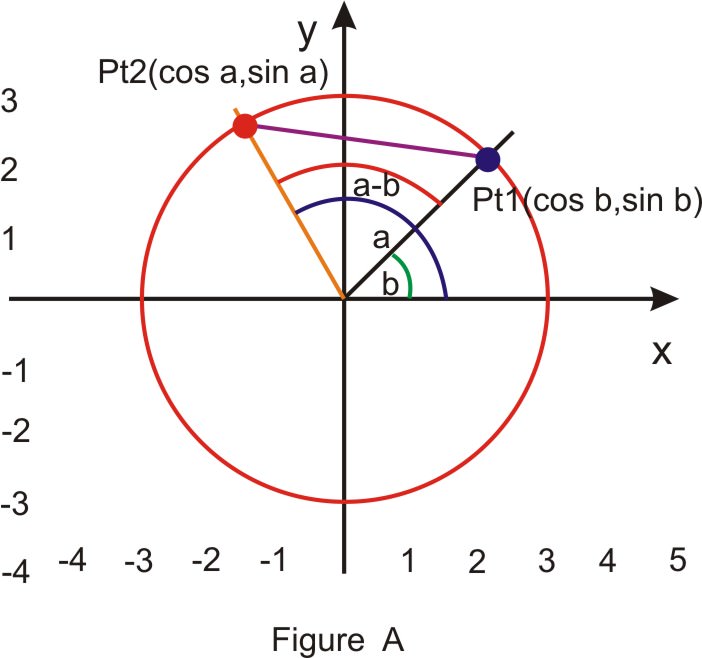
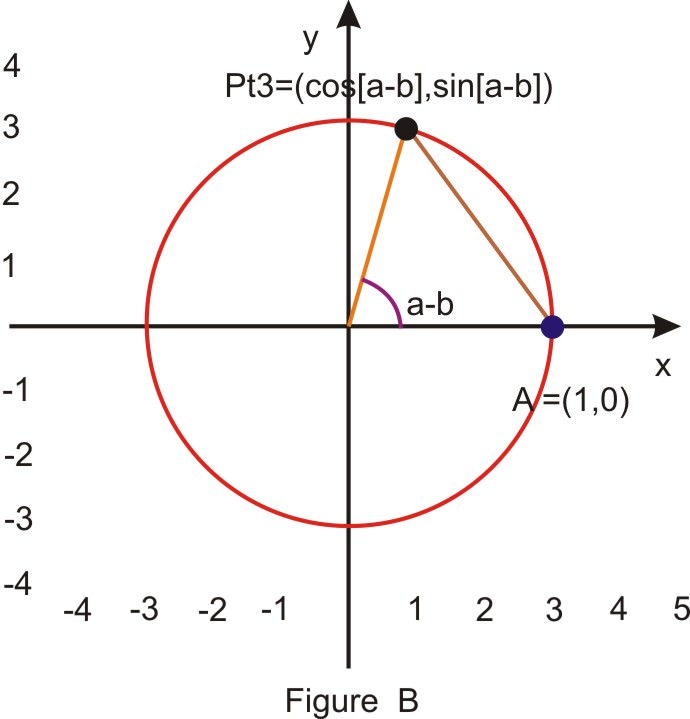
Triangles \(OP_{1} P_{2}\) in figure A and Triangle \(OAP_{3}\) in figure \(B\) are congruent. (Two sides and the included angle, \(a−b\), are equal). Therefore the unknown side of each triangle must also be equal. That is: \(d (A, P_3)=d (P_1,\; P_2)\)
Applying the distance formula to the triangles in Figures A and B and setting them equal to each other:
\(\sqrt{[\cos (a−b)−1]^2+[\sin (a−b)−0]^2}=\sqrt{(\cos a−\cos b)^2+(\sin a−\sin b)^2}\)
Square both sides to eliminate the square root.
\([\cos (a−b)−1]^2+[\sin (a−b)−0]^2=(\cos a−\cos b)^2+(\sin a−\sin b)^2\)
FOIL all four squared expressions and simplify.
\(\begin{aligned}
\cos ^{2}(a-b)-2 \cos (a-b)+1+\sin ^{2}(a-b) &=\cos ^{2} a-2 \cos a \cos b+\cos ^{2} b+\sin ^{2} a-2 \\
\underbrace{\sin ^{2}(a-b)+\cos ^{2}(a-b)}-2 \cos (a-b)+1 &=\underbrace{\sin ^{2} a+\cos ^{2} a}-2 \cos a \cos b+\underbrace{\sin ^{2} b+\cos ^2 b} -2\sin a \sin b \end{aligned}\)
\(\begin{aligned} 2\cos(a-b) + 1&=1-2 \cos a \cos b+1-2 \sin a \sin b \\
2-2 \cos (a-b) &=2-2 \cos a \cos b-2 \sin a \sin b \\
-2 \cos (a-b) &=-2 \cos a \cos b-2 \sin a \sin b \\
\cos (a-b) &=\cos a \cos b+\sin a \sin b
\end{aligned}\)
In \(\cos (a−b)=\cos a\cos b+\sin a\sin b\), the difference formula for cosine, you can substitute \(a−(−b)=a+b\) to obtain: \(\cos (a+b)=\cos [a−(−b)]\) or \(\cos a\cos (−b)+\sin a\sin (−b)\). since \(\cos (−b)=\cos b\) and \(\sin (−b)=−\sin b\), then \(\cos (a+b)=\cos a\cos b−\sin a\sin b\), which is the sum formula for cosine.
using the cosine Difference Formula
1. Find an equivalent form of \(\cos \left(\dfrac{\pi}{2}−\theta \right)\) using the cosine difference formula.
\(\begin{aligned} \cos \left(\dfrac{\pi}{2}−\theta \right) &=\cos \dfrac{\pi}{2}\cos \theta +\sin \dfrac{\pi}{2} \sin \theta \\ \cos \left(\dfrac{\pi}{2}−\theta \right)&=0 \times \cos \theta +1\times \sin \theta , \text{ substitute } \cos \dfrac{\pi}{2}=0 \text{ and } \sin \dfrac{\pi}{2}=1\\ \cos \left(\dfrac{\pi}{2}−\theta \right) &=\sin \theta \end{aligned}\)
We know that is a true identity because of our understanding of the sine and cosine curves, which are a phase shift of \(\dfrac{\pi}{2}\) off from each other.
The cosine formulas can also be used to find exact values of cosine that we weren’t able to find before, such as \(15^{\circ} =(45^{\circ} −30^{\circ})\), \(75^{\circ} =(45^{\circ} +30^{\circ} )\), among others.
2. Find the exact value of \(\cos 15^{\circ}\)
Use the difference formula where \(a=45^{\circ}\) and \(b=30^{\circ}\).
\(\begin{aligned} \cos (45^{\circ} −30^{\circ} ) &=\cos 45^{\circ} \cos 30^{\circ} +\sin 45^{\circ} \sin 30^{\circ} \\ \cos 15^{\circ}&=\dfrac{\sqrt{2}}{2}\times \dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{2}\times \dfrac{1}{2} \\ \cos 15^{\circ}&=\dfrac{\sqrt{6}+\sqrt{2}}{4} \end{aligned}\)
3. Find the exact value of \(\cos \dfrac{5 \pi}{12}\), in radians.
\(\cos \dfrac{5 \pi}{12}=\cos \left(\dfrac{\pi}{4}+\dfrac{\pi}{6}\right)\), notice that \(\dfrac{\pi}{4}=\dfrac{3 \pi}{12}\) and \(\dfrac{\pi}{6}=\dfrac{2 \pi}{12}\)
\(\begin{aligned} \cos \left(\dfrac{\pi}{4}+\dfrac{\pi}{6}\right) &=\cos \dfrac{\pi}{4}\cos \dfrac{\pi}{6}−\sin \dfrac{\pi}{4}\sin \dfrac{\pi}{6} \\ \cos \dfrac{\pi}{4}\cos \dfrac{\pi}{6}−\sin \dfrac{\pi}{4}\sin \dfrac{\pi}{6}&=\dfrac{\sqrt{2}}{2}\times \dfrac{\sqrt{3}}{2}−\dfrac{\sqrt{2}}{2}\times \dfrac{1}{2} \\&=\dfrac{\sqrt{6}−\sqrt{2}}{4} \end{aligned}\)
Earlier, you were asked if you can calculate the cosine of the difference between the two angles.
Solution
It would seem that your friend was having some fun with you, since he figured you didn't know the cosine difference formula. But now, with this formula in hand, you can readily solve for the difference of the two angles:
\(\begin{aligned} \cos (110^{\circ} −80^{\circ} ) &=(\cos 110^{\circ} )(\cos 80^{\circ} )+(\sin 110^{\circ} )(\sin 80^{\circ} ) \\&=(−.342)(.174)+(.9397)(.9848) \\&=−.0595+.9254=.8659\end{aligned}\)
Therefore,
\(\cos \left(110^{\circ} −80^{\circ} \right)=.8659\)
Find the exact value for \(\cos \dfrac{5 \pi}{12}\)
Solution
\(\begin{aligned} \cos \dfrac{5 \pi}{12}&=\cos \left(\dfrac{2 \pi}{12}+\dfrac{3 \pi}{12}\right) \\&=\cos \left(\dfrac{\pi}{6}+\dfrac{\pi}{4}\right)=\cos \dfrac{\pi}{6}\cos \dfrac{\pi}{4}−\sin \dfrac{\pi}{6}\sin \dfrac{\pi}{4}=\dfrac{\sqrt{3}}{2}\cdot \dfrac{\sqrt{2}}{2}−12\cdot \dfrac{\sqrt{2}}{2}=\dfrac{\sqrt{6}}{4}−\dfrac{\sqrt{2}}{4}=\sqrt{6}−\dfrac{\sqrt{2}}{4} \end{aligned}\)
Find the exact value for \(\cos \dfrac{7 \pi}{12}\)
Solution
\(\begin{aligned}\cos \dfrac{7 \pi}{12}&=\cos \left(\dfrac{4 \pi}{12}+\dfrac{3 \pi}{12}\right) \\ &=\cos \left(\dfrac{ \pi}{3}+\dfrac{\pi}{4}\right) \\ &=\cos \dfrac{ \pi}{3}\cos \dfrac{\pi}{4}−\sin \dfrac{ \pi}{3}\sin \dfrac{\pi}{4} \\&=12\cdot \dfrac{\sqrt{2}}{2}−\dfrac{\sqrt{3}}{2}\cdot \dfrac{\sqrt{2}}{2} \\&=\dfrac{\sqrt{2}}{4}−\dfrac{\sqrt{6}}{4} \\&=\dfrac{\sqrt{2}−\sqrt{6}}{4} \end{aligned}\)
Find the exact value for \(\cos 345^{\circ}\)
Solution
\(\begin{aligned} \cos 345^{\circ} &=\cos (315^{\circ} +30^{\circ} ) \\&=\cos 315^{\circ} \cos 30^{\circ} −\sin 315^{\circ} \sin 30^{\circ} \\&=\dfrac{\sqrt{2}}{2}\cdot \dfrac{\sqrt{3}}{2}−\left(−\dfrac{\sqrt{2}}{2}\right)\cdot \dfrac{1}{2} \\&=\dfrac{\sqrt{6}+\sqrt{2}}{4} \end{aligned}\)
Review
Find the exact value for each cosine expression.
- \(\cos 75^{\circ}\)
- \(\cos 105^{\circ}\)
- \(\cos 165^{\circ}\)
- \(\cos 255^{\circ}\)
- \(\cos −15^{\circ}\)
Write each expression as the cosine of an angle.
- \(\cos 96^{\circ} \cos 20^{\circ} +\sin 96^{\circ} \sin 20^{\circ}\)
- \(\cos 4x\cos 3x−\sin 4x\sin 3x\)
- \(\cos 37^{\circ} \cos 12^{\circ} +\sin 37^{\circ} \sin 12^{\circ}\)
- \(\cos 59^{\circ} \cos 10^{\circ} −\sin 59^{\circ} \sin 10^{\circ}\)
- \(\cos 5y\cos 2y+\sin 5y\sin 2y\)
- Prove that \(\cos \left(x−\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}(\cos (x)+\sin (x))\)
- If \(\cos (x)\cos (y)=\sin (x)\sin (y)\), then what does \(\cos (x+y)\) equal?
- Prove that \(\cos \left(x−\dfrac{\pi}{2}\right)=\sin (x)\)
- Use the fact that \(\cos \left(\dfrac{\pi}{2}−x\right)=\sin (x)\) (shown in examples), to show that \(\sin \left(\dfrac{\pi}{2}−x \right)=\cos (x)\).
- Prove that \(\cos (x−y)+\cos (x+y)=2\cos (x)\cos (y)\).
Review (Answers)
To see the Review answers, open this PDF file and look for section 3.6.

