4.2.3: Determination of Unknown Triangle Measures Given Area
- Page ID
- 4166
Solve for missing triangle parts using area formulas and the law of cosines/sines.
You are working on creating a mobile for your art class. A mobile is a piece of art that has a rod with different shapes hanging from it, so they can spin.
To create your project, you need to cut a set of triangles that have a variety of sizes. You are about to start cutting triangles, when your friend, who is helping you with the project, comes over. She tells you that each piece needs to have a rod through the side of it to balance the shape in a certain way. She wants you to make a piece that looks like this:
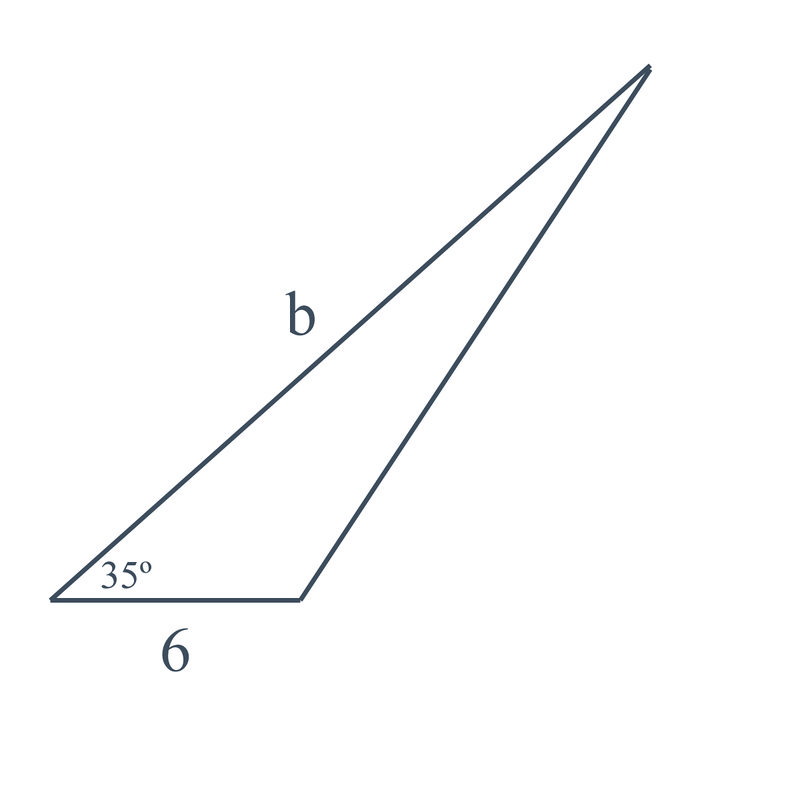
You have already cut a triangle by cutting a piece out of construction paper. You know that one side of your triangle is 6 inches long, but you don't know the length of the other two sides. Can you use the information you have to find the length of b in the mobile piece above? (The area of the triangle is \(25\text{ in}^2 \), and the interior angle between the six inch side and the side you want to know is \(35^{\circ} \)).
Finding the Measures of a Triangle Given the Area
In this section, we will look at situations where we know the area but need to find another part of the triangle, as well as an application involving a quadrilateral. All of this will involve the use of the Law of Cosines, Law of Sines, and the Alternate Formula for the Area of a Triangle.
1. The jib sail on a sailboat came untied and the rope securing it was lost. If the area of the jib sail is 56.1 square feet, use the figure and information below to find the length of the rope.
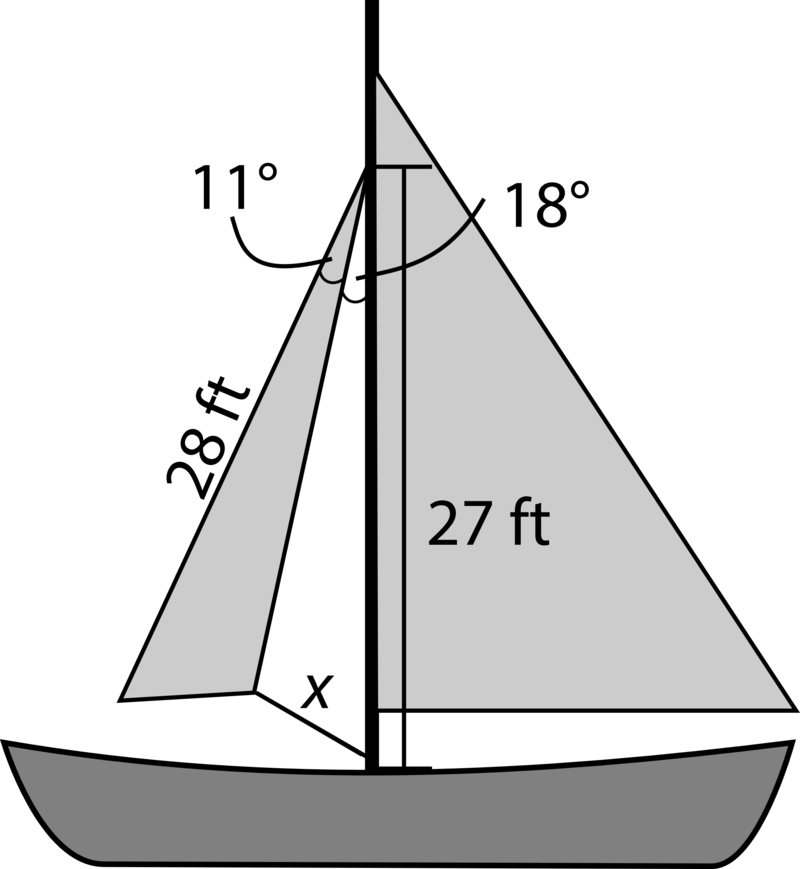
Since we know the area, one of the sides, and one angle of the jib sail, we can use the formula \(K=\dfrac{1}{2} bc \sin A\) to find the side of the jib sail that is attached to the mast. We will call this side \(y\).
\(\begin{aligned} 56.1 &=\dfrac{1}{2} 28(y)\sin 11\\ 56.1 &=2.671325935 y\\ 21.0&=y \end{aligned}\)
Now that we know side y, we know two sides and the included angle in the triangle formed by the mast, the rope, and the jib sail. We can now use the Law of Cosines to calculate the length of the rope.
\(\begin{aligned} x^2 &=21^2+27^2−2(21)(27)\cos 18 \\ x^2&=91.50191052 \\ x&\approx 9.6\text{ ft}\end{aligned}\)
The length of the rope is approximately 9.6 feet.
2. In quadrilateral \(QUAD\) below, the area of \(\Delta QUD=5.64\), the area of \(\Delta UAD=6.39\), \(\angle QUD=31^{\circ} \), \(\angle DUA=40^{\circ} \), and \(UD=7.8\). Find the perimeter of \(QUAD\).
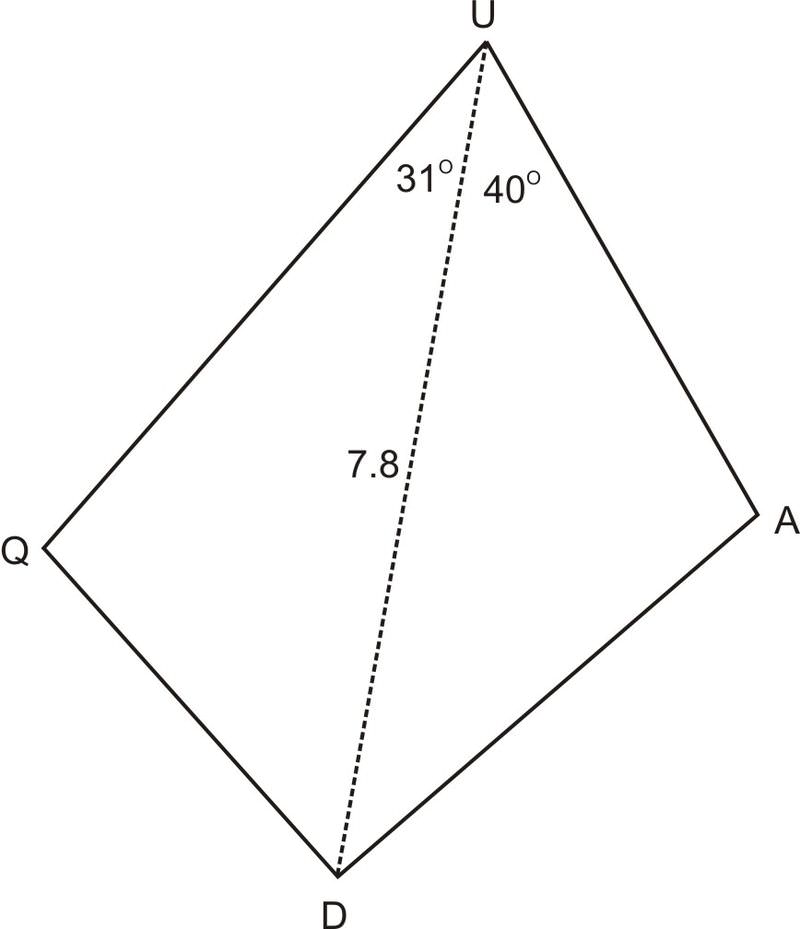
In order to find the perimeter of \(QUAD\), we need to know sides \(QU\), \(QD\), \(UA\), and \(AD\). Since we know the area, one side, and one angle in each of the triangles, we can use \(K=\dfrac{1}{2} bc \sin A\) to figure out \(QU\) and \(UA\).
\(\begin{aligned}
5.64 & =\dfrac{1}{2}(7.8)(Q U) \sin 31 & 6.39&=\dfrac{1}{2}(7.8) U A \sin 40 \\
2.8 & \approx Q U & 2.5 &\approx U A
\end{aligned}\)
Now that we know QU and UA, we know two sides and the included angle in each triangle (SAS). This means that we can use the Law of Cosines to find the other two sides, QD and DA. First we will find QD and DA.
\(\begin{aligned}
Q D^{2}&=2.8^{2}+7.8^{2}-2(2.8)(7.8) \cos 31 & D A^{2}&=2.5^{2}+7.8^{2}-2(2.5)(7.8) \cos 40 \\
Q D^{2}&=31.23893231 & D A^{2}&=37.21426672 \\
Q D& \approx 5.6 & D A &\approx 6.1
\end{aligned}\)
Finally, we can calculate the perimeter since we have found all four sides of the quadrilateral.
\(pQUAD=2.8+5.6+6.1+2.5=17\)
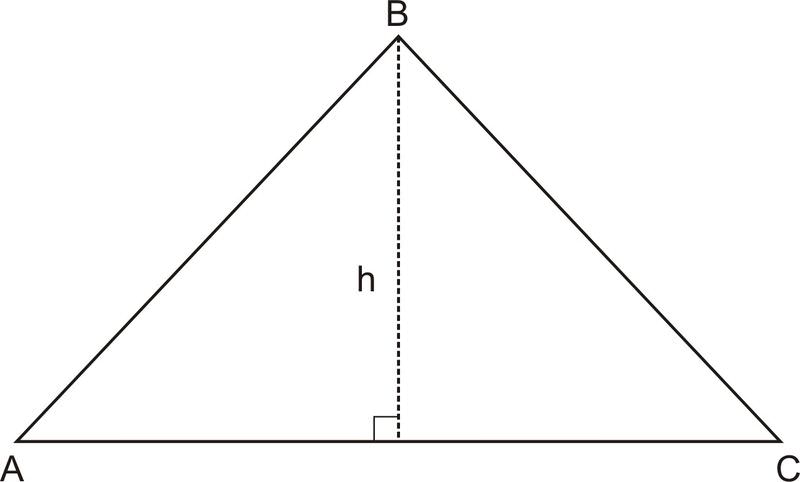
3. In \(\Delta ABC\), \(BD\) is an altitude from \(B\) to \(AC\). The area of \(\Delta ABC=232.96\), \(AB=16.2\), and \(AD=14.4\). Find \(DC\).
First, find BD by using the Pythagorean Theorem. \(BD=\sqrt{16.2^2−14.4^2}=7.42\). Then, using the area and formula (\(A=\dfrac{1}{2}bh\)), you can find \(AC\).
\(232.96=\dfrac{1}{2}(7.42)AC\rightarrow AC=62.78. \; DC=62.78−14.4=48.38\).
Earlier, you were asked to find the length of \(b\) in the mobile piece.
Solution
Since you know that the mobile piece is six inches on one side, and that the area of the triangle is \(25\text{ in}^2 \), you can use the formula \(K=\dfrac{1}{2} ab \sin C\) to find the length of the other side:
\(\begin{aligned} K&=\dfrac{1}{2} ab \sin C \\ 25&=\dfrac{1}{2} (6)(b)\sin 35^{\circ} \\ 25&=1.72b \\ b&=\dfrac{25}{1.72 }\\ b&=14.53\text{ in}\end{aligned}\)
Find "\(h\)" in the triangle below: \(\text{Area} =1618.98\), \(b=36.3\)
Solution
Since we know the area, one of the sides (18.15), and one angle of the triangle (\(45^{\circ} \)), we can use the formula \(K=\dfrac{1}{2} bc \sin A\) to find the other side of the triangle. We can then use the Pythagorean Theorem to find the height of the triangle.
This gives a result of:
\(h=89.2\)
Find \(\angle A\) in the triangle below: \(\text{Area }=387.6\), \(b=25.6\), \(c=32.9\)
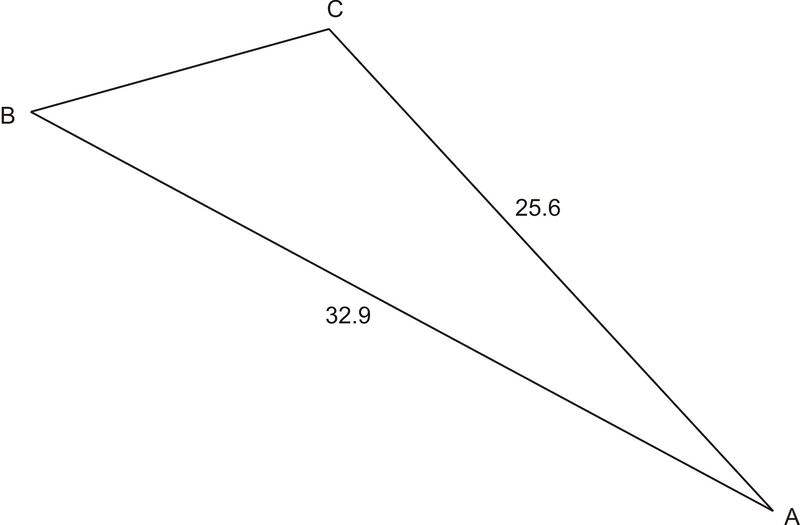
Solution
Since we know the area and the lengths of two of the sides of the triangle, we can use the formula \(K=\dfrac{1}{2} bc\sin A\) to solve for the included angle, which gives:
\(\angle A=67^{\circ}\)
Find the area of \(\Delta ABC\) below: \(\text{Area} \Delta ABD=16.96\), \(AD=3.2\), \(\angle DBC=49.6^{\circ} \)
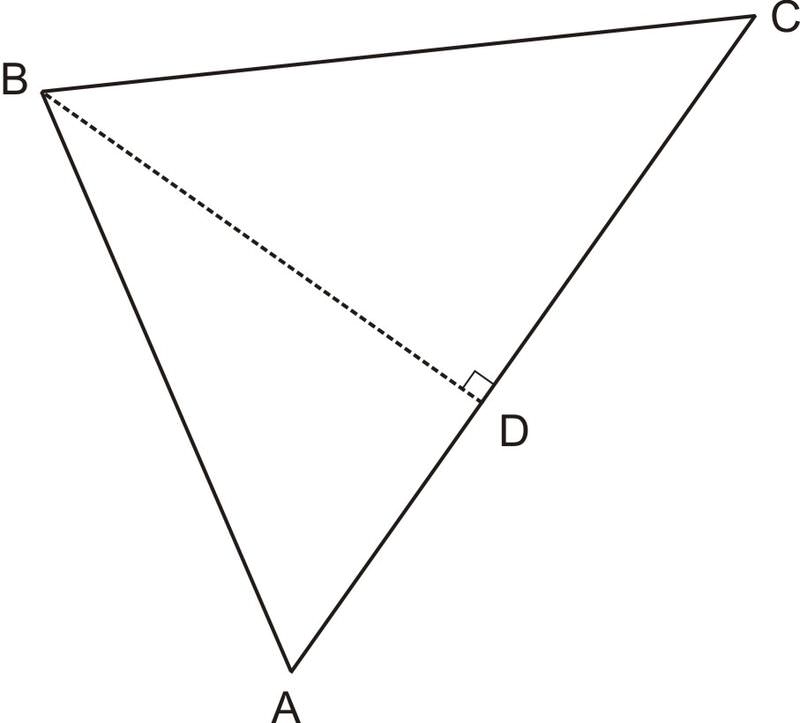
Solution
\(\text{Area of } \Delta ABC=83.0\)
Review
- The area of the triangle below is \(138\text{ in}^2 \). Solve for \(x\), the height.
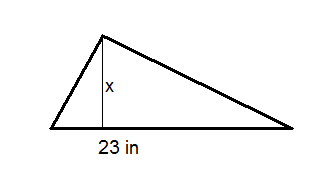
Figure \(\PageIndex{7}\) - The area of the triangle below is \(250\text{ cm}^2 \). A height is given on the diagram. Solve for \(x\).
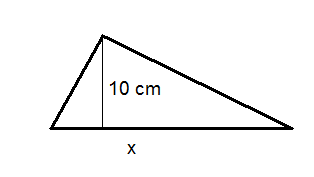
Figure \(\PageIndex{8}\)
Use the triangle below for questions 3-5. The area of the large triangle is \(65 \text{ cm}^2\).
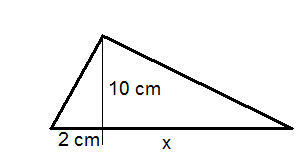
- Solve for \(x\).
- Find the perimeter of the large triangle.
- Find the measure of all three angles of the large triangle.
Use the triangle below for questions 6-8. The area of the triangle is \(244 \text{ cm}^2\).
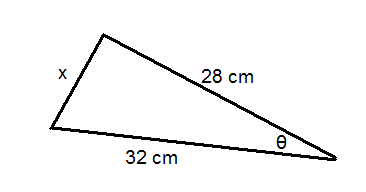
- Solve for \(\theta \).
- Solve for \(x\).
- Find the perimeter of the triangle.
Use the triangle below for questions 9-11. The area of the triangle is \(299.8 \text{ in}^2\).
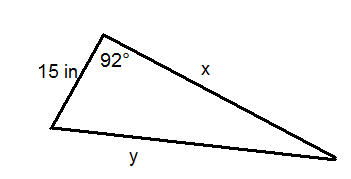
- Solve for \(x\).
- Solve for \(y\).
- Find the measure of the other two angles of the triangle.
Use the triangle below for questions 12-15. The area of the large triangle is \(84 \text{ in}^2\).
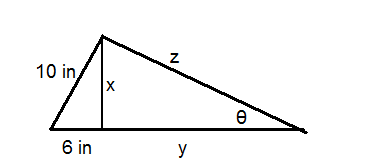
- Solve for \(x\).
- Solve for \(y\).
- Solve for \(z\).
- Solve for \(\theta \).
Review (Answers)
To see the Review answers, open this PDF file and look for section 5.6.
Vocabulary
| Term | Definition |
|---|---|
| law of cosines | The law of cosines is a rule relating the sides of a triangle to the cosine of one of its angles. The law of cosines states that \(c^2=a^2+b^2−2ab\cos C\), where \(C\) is the angle across from side \(c\). |
| law of sines | The law of sines is a rule applied to triangles stating that the ratio of the sine of an angle to the side opposite that angle is equal to the ratio of the sine of another angle in the triangle to the side opposite that angle. |

