5.1.2: Distance Between Two Polar Coordinates

Application of the law of cosines.

Distance Between Two Polar Coordinates

When playing a game of darts with your friend, the darts you throw land in a pattern like this

Figure \(\PageIndex{1}\)

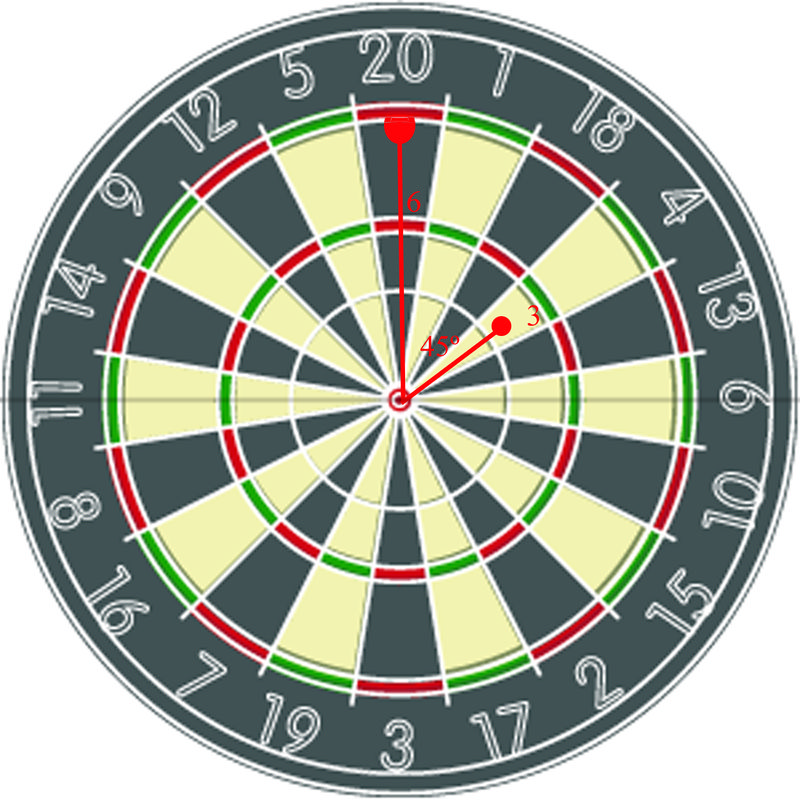
You and your friend decide to find out how far it is between the two darts you threw. If you know the positions of each of the darts in polar coordinates, can you somehow find a formula to let you determine the distance between the two darts?

Finding the Distance Between Two Polar Coordinates

Just like the Distance Formula for x and y coordinates, there is a way to find the distance between two polar coordinates. One way that we know how to find distance, or length, is the Law of Cosines, \(a^2=b^2+c^2−2bc\cos A\) or \(a=\sqrt{b^2+c^2−2bc\cos A}\). If we have two points \((r_1,\theta _1)\) and \((r_2,\theta _2)\), we can easily substitute r1 for b and r2 for c. As for A, it needs to be the angle between the two radii, or \((\theta _2−\theta _1)\). Finally, a is now distance and you have \(d=r^2_1+r^2_2−2r_1r_2 \cos(\theta _2−\theta _1)\).

Finding the Distance

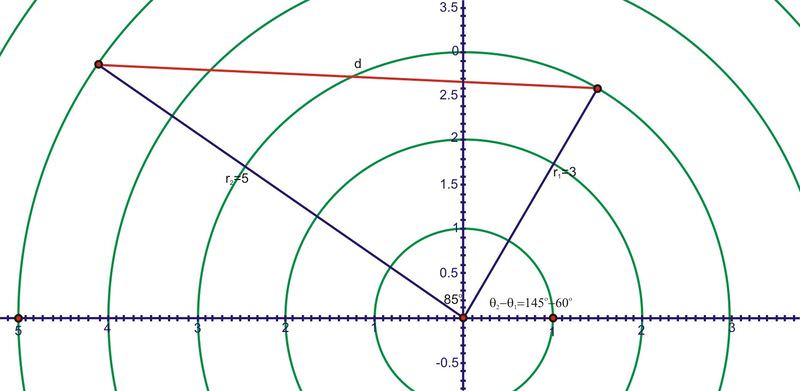
1. Find the distance between \((3,60^{\circ} )\) and \((5,145^{\circ} )\).

After graphing these two points, we have a triangle. Using the new Polar Distance Formula, we have \(d=\sqrt{3^2+5^2−2(3)(5)\cos 85^{\circ} }\approx 5.6\).

Figure \(\PageIndex{2}\)

2. Find the distance between \((9,−45^{\circ} )\) and (\(−4,70^{\circ} \)).

This one is a little trickier than the last #1 because we have negatives. The first point would be plotted in the fourth quadrant and is equivalent to \((9,315^{\circ} )\). The second point would be \((4,70^{\circ} )\) reflected across the pole, or \((4,250^{\circ} )\). Use these two values of \theta for the formula. Also, the radii should always be positive when put into the formula. That being said, the distance is \(d=9^2+4^2−2(9)(4)\cos (315−250)^{\circ} \approx 8.16\).

3. Find the distance between \((2,10^{\circ} )\) and \((7,10^{\circ} )\).

This problem is straightforward from looking at the relationship between the points. The two points lie at the same angle, so the straight line distance between them is 7−2=5. However, we can confirm this using the distance formula:

\(d=\sqrt{2^2+7^2−2(2)(7)\cos 0^{\circ} }=\sqrt{4+49−28}=\sqrt{25}=5\).

Example \(\PageIndex{1}\)

Earlier, you were asked to find the distance between the two darts.

Using the Distance Formula for points in a polar plot, it is possible to determine the distance between the 2 darts:

Solution

\(\begin{aligned} d&=\sqrt{3^2+6^2−2(4)(6)\cos 45^{\circ} } \\ d&=\sqrt{9+36−48(.707)} \\ d&=\sqrt{45−33.936} \\ d&\approx 11.064 \end{aligned}\)

Example \(\PageIndex{2}\)

Given P1 and P2, calculate the distance between the points.

\(P_1(1,30^{\circ} )\) and \(P_2(6,135^{\circ} )\)

Solution

Use \(P_1P_2=\sqrt{r^2_1+r^2_2−2r_1r_2\cos (\theta _2−\theta _1)}\).

\(\begin{aligned} P_1P_2&=1^2+6^2−2(1)(6)\cos (135^{\circ} −30^{\circ} ) \\ P_1P_2 &\approx 6.33 \text{ units}\end{aligned} \)

Example \(\PageIndex{3}\)

Given \(P_1\) and \(P_2\), calculate the distance between the points.

\(P_1(2,−65^{\circ} )\) and \(P_2(9,85^{\circ} )\)

Solution

Use \(P_1P_2=\sqrt{r^2_1+r^2_2−2r_1r_2\cos (\theta _2−\theta _1)}\).

\(P_1P_2=\sqrt{2^2+9^2−2(2)(9)\cos 150^{\circ} }=10.78\)

Example \(\PageIndex{4}\)

Given \((P_1\) and \(P_2\), calculate the distance between the points.

\(P_1(−3,142^{\circ} )\) and \(P_2(10,−88^{\circ} )\)

Solution

3. Use \(P_1P_2=\sqrt{r^2_1+r^2_2−2r_1r_2\cos (\theta _2−\theta _1)}\).

\(\begin{aligned} P_1P_2&=\sqrt{3^2+10^2−2(3)(10) \cos(322−272)^{\circ} } \\ &=8.39 \end{aligned}\)

Review

Find the distance between each set of points.

1. \((1,150^{\circ} )\) and \((2,130^{\circ} )\)
2. \((4,90^{\circ} )\) and \((5,210^{\circ} )\)
3. \((6,60^{\circ} )\) and \((2,90^{\circ} )\)
4. \((2,120^{\circ} )\) and \((1,150^{\circ} )\)
5. \((7,210^{\circ} )\) and \((4,300^{\circ} )\)
6. \((−4,120^{\circ} )\) and \((2,100^{\circ} )\)
7. \((3,−90^{\circ} )\) and \((5,150^{\circ} )\)
8. \((−4,−30^{\circ} )\) and \((3,250^{\circ} )\)
9. \((7,−150^{\circ} )\) and \((4,130^{\circ} )\)
10. \((−2,300^{\circ} )\) and \((2,10^{\circ} )\)
11. Find the length of the arc between the points \((3,40^{\circ} )\) and \((3,150^{\circ} )\).
12. Find the length of the arc between the points \((1,10^{\circ} )\) and \((1,70^{\circ} )\).
13. Find the area of the sector created by the origin and the points \((4,20^{\circ} )\) and \((4,110^{\circ} )\).
14. Find the area of the sector created by the origin and the points \((2,100^{\circ} )\) and \((2,180^{\circ} )\).
15. Find the area of the sector created by the origin and the points \((5,110^{\circ} )\) and \((5,160^{\circ} )\).

Review (Answers)

To see the Review answers, open this PDF file and look for section 6.2.

Additional Resources

Interactive Element

Practice: Distance Between Two Polar Coordinates