5.2.3: Rectangular to Polar Form for Equations
- Page ID
- 4179
Convert equations by substituting x and y with expressions of distance and angles.
You are working diligently in your math class when your teacher gives you an equation to graph:
\((x+1)^2−(y+2)^2=7\)
As you start to consider how to rearrange this equation, you are told that the goal of the class is to convert the equation to polar form instead of rectangular form.
Can you find a way to do this?
Rectangular Equations to Polar Form
Interestingly, a rectangular coordinate system isn't the only way to plot values. A polar system can be useful. However, it will often be the case that there are one or more equations that need to be converted from rectangular to polar form. To write a rectangular equation in polar form, the conversion equations of \(x=r\cos \theta\) and \(y=r\sin \theta\) are used.
If the graph of the polar equation is the same as the graph of the rectangular equation, then the conversion has been determined correctly.
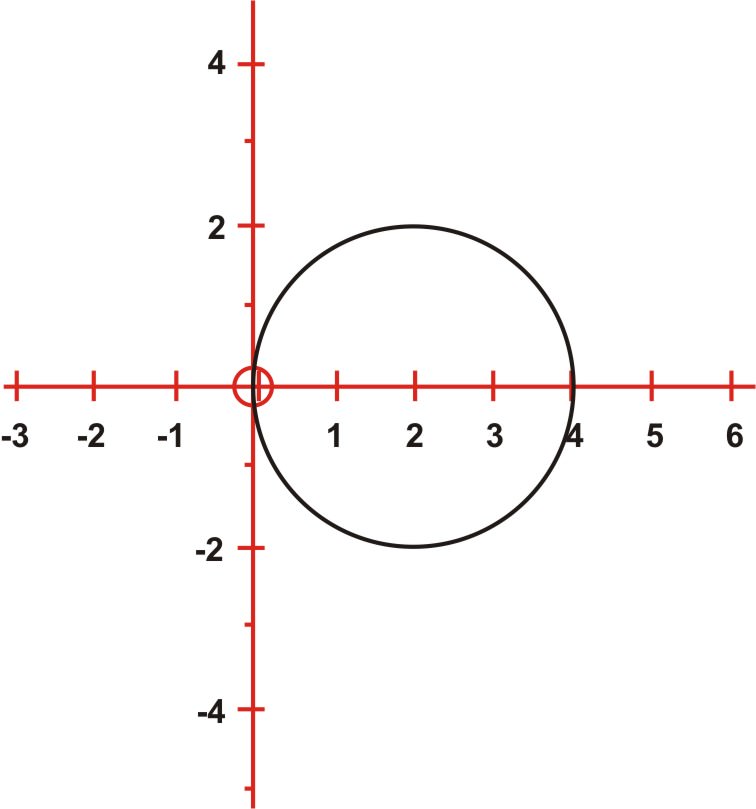
\((x−2)^2+y^2=4\)
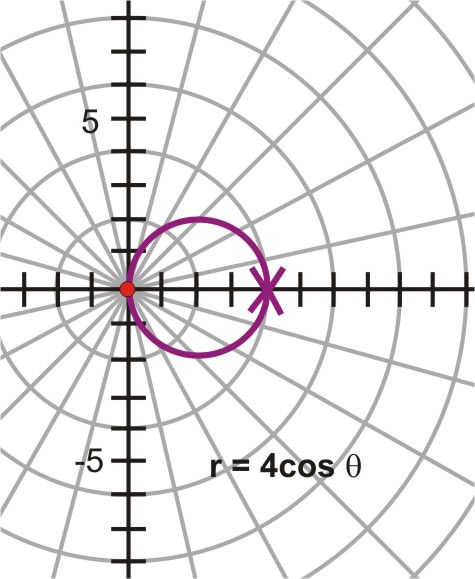
The rectangular equation \((x−2)^2+y^2=4\) represents a circle with center \((2, 0)\) and a radius of 2 units. The polar equation \(r=4\cos \theta\) is a circle with center \((2, 0)\) and a radius of 2 units.
Converting Equations
1. Write the rectangular equation \(x^2+y^2=2x\) in polar form.
Remember \(r=\sqrt{x^2+y^2}\), \(r^2=x^2+y^2\) and \(x=r\cos \theta\).
\(\begin{aligned} x^2+y^2 &=2x\\ r^2 &=2(r\cos \theta) &&\text{Pythagorean Theorem }\\ r^2 &=2r\cos \theta\\ r&=2\cos \theta and x=r\cos \theta && \text{Divide each side by r}\end{aligned}\)
2. Write \((x−2)^2+y^2=4\) in polar form.
Remember \(x=r\cos \theta\) and \(y=r\sin \theta\).
\(\begin{aligned} (x-2)^{2}+y^{2}&=4 \\ (r \cos \theta-2)^{2}+(r \sin \theta)^{2}&=4 && x=r \cos \theta \text{ and} y=r \sin \theta \\ r^{2} \cos ^{2} \theta-4 r \cos \theta+4+r^{2} \sin ^{2} \theta&=4 && \text{expand the terms} \\ r^{2} \cos ^{2} \theta-4 r \cos \theta+r^{2} \sin ^{2} \theta&=0 && \text{subtract 4 from each side}\\ r^{2} \cos ^{2} \theta+r^{2} \sin ^{2} \theta&=4 r \cos \theta && \text{isolate the squared terms} \\ r^{2}\left(\cos ^{2} \theta+\sin ^{2} \theta\right)&=4 r \cos \theta && \text{factor } r^{2}\text{ -a common factor} \\
r^{2}&=4 r \cos \theta && \text{ Pythagorean Identity } \\ r&=4 \cos \theta && \text{ Divide each side by } r \end{aligned}\)
3. Write the rectangular equation \((x+4)^2+(y−1)^2=17\) in polar form.
\(\begin{aligned} (x+4)^{2}+(y-1)^{2}&=17 \\ (r \cos \theta+4)^{2}+(r \sin \theta-1)^{2}&=17 && x=r \cos \theta \text{ and } y=r \sin \theta \\ r^{2} \cos ^{2} \theta+8 r \cos \theta+16+r^{2} \sin ^{2} \theta-2 r \sin \theta+1&=17 && \text{ expand the terms} \\ r^{2} \cos ^{2} \theta+8 r \cos \theta-2 r \sin \theta+r^{2} \sin ^{2} \theta&=0 && \text{ subtract 17 from each side} \\ r^{2} \cos ^{2} \theta+r^{2} \sin ^{2} \theta&=-8 r \cos \theta+2 r \sin \theta && \text{isolate the squared terms} \\ r^{2}\left(\cos ^{2} \theta+\sin ^{2} \theta\right)&=-2 r(4 \cos \theta-\sin \theta) && \text{ factor } r^{2} \text{-a common factor} \\ r^{2}&=-2 r(4 \cos \theta-\sin \theta) && \text{ Pythagorean Identity} \\ r&=-2(4 \cos \theta-\sin \theta) && \text{ Divide each side by } r \end{aligned}\)
Earlier, you were asked to convert an equation to polar form.
Solution
The original equation to convert is:
\((x+1)^2−(y+2)^2=7\)
You can substitute \(x=r\cos \theta\) and \(y=r\sin \theta\) into the equation, and then simplify:
\(\begin{aligned}
(r \cos \theta+1)^{2}-(r \sin \theta+2)^{2}&=7 \\
\left(r^{2} \cos ^{2} \theta+2 r \cos \theta+1\right)-\left(r^{2} \sin ^{2} \theta+4 r \sin \theta+4\right)&=7 \\
r^{2}\left(\cos ^{2} \theta-\sin ^{2} \theta\right)+2 r(\cos \theta-2 \sin \theta)-3&=7 \\
r^{2}\left(\cos ^{2} \theta-\sin ^{2} \theta\right)+2 r(\cos \theta-2 \sin \theta)&=10
\end{aligned}\)
Write the rectangular equation \((x−4)^2+(y−3)^2=25\) in polar form.
Solution
\(\begin{aligned}
(x-4)^{2}+(y-3)^{2} &=25 \\
x^{2}-8 x+16+y^{2}-6 y+9 &=25 \\
x^{2}-8 x+y^{2}-6 y+25 &=25 \\
x^{2}-8 x+y^{2}-6 y &=0 \\
x^{2}+y^{2}-8 x-6 y &=0 \\
r^{2}-8(r \cos \theta)-6(r \sin \theta) &=0 \\
r^{2}-8 r \cos \theta-6 r \sin \theta &=0 \\
r(r-8 \cos \theta-6 \sin \theta) &=0 \\
r=0 \text { or } r-8 \cos \theta-6 \sin \theta &=0 \\
r=0 \text { or } r &=8 \cos \theta+6 \sin \theta
\end{aligned}\)
From graphing r−8\cos \theta−6\sin \theta=0, we see that the additional solutions are 0 and 8.
Write the rectangular equation \(3x−2y=1\) in polar form.
Solution
\(\begin{aligned} 3x−2y&=1 \\ 3r\cos \theta−2r\sin \theta &=1\\ r(3\cos \theta−2\sin \theta) &=1\\ r&=\dfrac{1}{3\cos \theta−2\sin \theta} \end{aligned}\)
Write the rectangular equation \(x^2+y^2−4x+2y=0\) in polar form.
Solution
\(\begin{aligned}
x^{2}+y^{2}-4 x+2 y &=0 \\
r^{2} \cos ^{2} \theta+r^{2} \sin ^{2} \theta-4 r \cos \theta+2 r \sin \theta &=0 \\
r^{2}\left(\sin ^{2} \theta+\cos ^{2} \theta\right)-4 r \cos \theta+2 r \sin \theta &=0 \\
r(r-4 \cos \theta+2 \sin \theta) &=0 \\
r=0 \text { or } r-4 \cos \theta+2 \sin \theta &=0 \\
r=0 \text { or } r &=4 \cos \theta-2 \sin \theta
\end{aligned}\)
Review
Write each rectangular equation in polar form.
- \(x=3\)
- \(y=4\)
- \(x^2+y^2=4\)
- \(x^2+y^2=9\)
- \((x−1)^2+y^2=1\)
- \((x−2)^2+(y−3)^2=13\)
- \((x−1)^2+(y−3)^2=10\)
- \((x+2)^2+(y+2)^2=8\)
- \((x+5)^2+(y−1)^2=26\)
- \(x^2+(y−6)^2=36\)
- \(x^2+(y+2)^2=4\)
- \(2x+5y=11\)
- \(4x−7y=10\)
- \(x+5y=8\)
- \(3x−4y=15\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 6.6.
Additional Resources
Video: Example: Find the Polar Equation for a Line
Practice: Rectangular to Polar Form for Equations

