5.2.6: Systems of Polar Equations
- Page ID
- 4182
Points of intersection or locations where two polar equations have the same solution.
You likely recall that when you graph multiple equations on the same line, you usually end up with locations on the graph where they intersect (unless you are graphing parallel lines!).
The same is true when graphing equations in polar form, and/or on a polar graph. When you graph the intersection of multiple polar equations, you treat them just as you would rectangular equations, graph both and find the areas that are true for both equations.
Systems of Polar Equations
Polar equations can be graphed using polar coordinates. Graphing two polar equations on the same set of axes may result in having point(s) of intersection.
All points on a polar graph are coordinates that make the equation valid. The coordinates of point(s) of intersection when substituted into each equation will make both of the equations valid.
One method to find point(s) of intersection for two polar graphs is by setting the equations equal to each other.
Call the first equation \(r_1 \) and the second equation \(r_2 \).
Points of intersection are when \(r_1 = r_2 \), so set the equations equal and then solve the resulting trigonometric equation.
Find the intersection of \(r_1 =3 \sin \theta \) and \(r_2 =\sqrt{3} \cos \theta \).
Solution
Set the equations equal to each other: \(3 \sin \theta =\sqrt{3} \cos \theta\)
divide both sides of the equation by cos \(\theta \) and 3: \(\dfrac{3 \sin \theta }{3\cos \theta }=\dfrac{\sqrt{3} \cos \theta }{3 \cos \theta}\)
Simplify: \(\dfrac{\sin \theta }{\cos \theta }=\dfrac{\sqrt{3} }{3}\)
Use the identity: \(\dfrac{\sin \theta }{\cos \theta }=\tan \theta\)
\(\tan \theta =\dfrac{\sqrt{3}}{ 3}\)
\(\theta =\dfrac{\pi }{6}\) or \(\dfrac{7\pi }{6}\)
substitute \(\dfrac{\pi }{6}\) in either equation to obtain \(r = 1.5\)
substitute \(\dfrac{7\pi }{6}\) in either equation to obtain \(-1.5\)
NOTE: the coordinates \(\left(1.5, \dfrac{\pi }{6}\right)\) and \(\left(−1.5, \dfrac{7\pi }{6}\right)\) represent the SAME polar point so there is only one solution to this equation.
Are we done? If we look at the graphs of \(r_1 \) and \(r_2 \), we can see that there is another point of intersection:
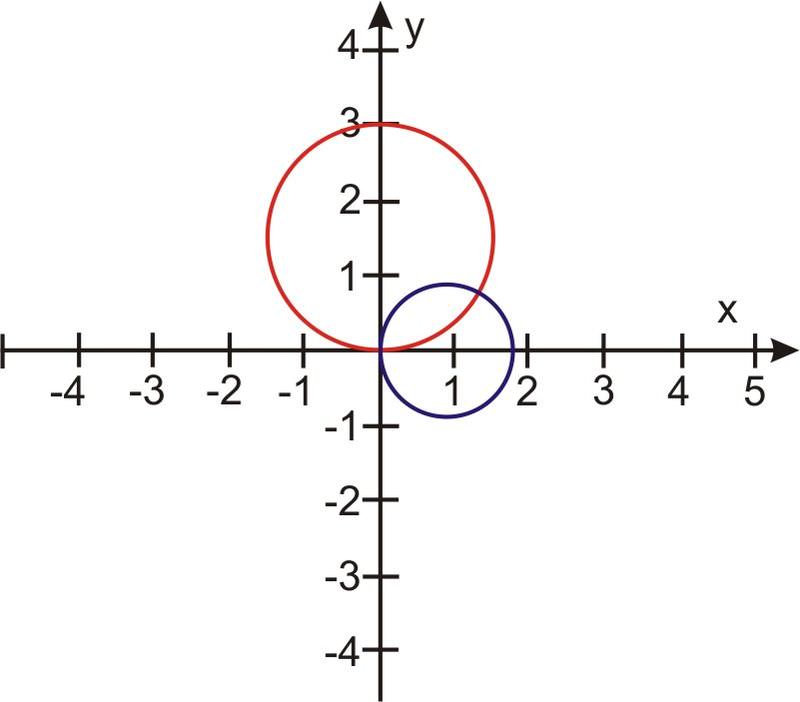
when \(\theta = 0\), \(r_1 = 3 \) sin \(\theta = 3 \) sin \((0) = 0\)
That means \(r_1 = 3 \) sin \(\theta\) goes through the pole \((0, 0)\).
For r_2 : when \(\theta =\dfrac{\pi }{2}\), \(r_2 = 0\) that is \(r_2 =\sqrt{3} \cos \theta \) goes through the point \(\left(0,\dfrac{\pi }{2}\right)\).
Therefore, both graphs go through the pole and the pole is a point of intersection.
The pole was NOT revealed as a point of intersection using the first step! (Why? Hint: How many ways are there to represent the pole in polar coordinates?) This shows us that after you use algebraic methods to find intersections at points other than the pole, you should also check for intersections at the pole.
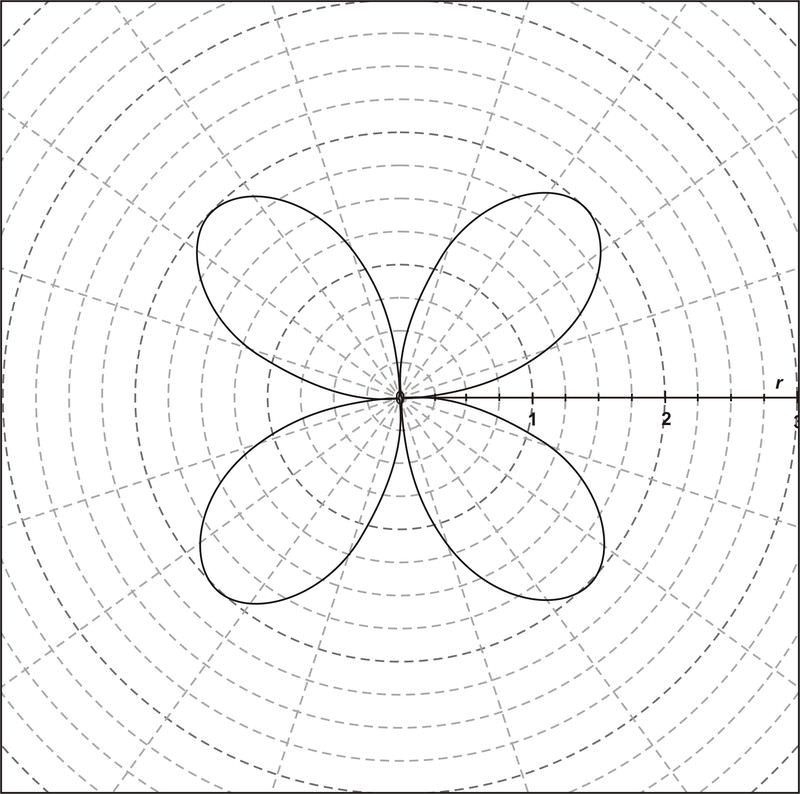
Find the point(s) of intersection for the two graphs: \(r_1 = 1\) and \(r_2 = 2 \sin 2\theta \).
Solution
Set \(r_1 = r_2\) and solve:
\(\begin{aligned} 1&=2 \sin 2\theta \\ \dfrac{1}{2}&=\sin 2\theta\end{aligned} \)
Use a substitution \(\alpha = 2\theta \) to solve
\(\begin{aligned} \dfrac{1}{2}&=\sin \alpha \\ \alpha &=\dfrac{\pi }{6}, \dfrac{5\pi }{6} \end{aligned}\)
Since \(\alpha = 2\theta \), solving for \(\theta \) gives us
\(\theta =\dfrac{\pi }{12}, \dfrac{5\pi }{12}\)
But, recall that \(\theta \) has the range \(0 \leq \theta \leq 2\pi \). Since we solved with \(0 \leq \alpha \leq 2\pi\) we actually need to consider values of \(\theta \) with \(0 \leq \theta \leq 4\pi \). Why? Recall that \(\sin (2\theta )\) has two cycles between \(0\) and \(2\pi \), and so we add two more solutions,
\(\alpha =\dfrac{13\pi }{6}, \dfrac{17\pi }{6}\)
and since \(\alpha = 2\theta \),
\(\theta =\dfrac{13\pi }{12}, \dfrac{17\pi }{12}\)
Finally, we need to consider solutions when \(r = -1\) because \(r = 1\) and \(r = -1\) are the same polar equation. So, solving
\(\begin{aligned} −\dfrac{1}{2}&=\sin \alpha \\ \alpha &=\dfrac{7\pi }{6}, \dfrac{11\pi }{6}\end{aligned}\)
Again, using \(\alpha = 2\theta \) and adding solutions for the repetition gives us four more solutions,
\(\theta =\dfrac{7\pi }{12}, \dfrac{11\pi }{12}, \dfrac{19\pi }{12}, \dfrac{21\pi}{12}\)
So in total, there are eight solutions to this set of equations.
NOTE: Recall that solving trigonometric equations where the angle is \theta requires looking at all potential values between 0 and \(2\pi \). When the angle is \(2\theta\) as it is in this case, be sure to look for all potential values between 0 and \(4\pi \). When the angle is \(3\theta\) as it is in this case, be sure to look for all potential values between 0 and \(6\pi \)., and so on.
Since \(r_1 \) cannot equal 0, the pole is not on its graph and not a point of intersection.
The graph reveals eight points of intersection which were found earlier.
Find point(s) of intersection, if any exist, for the following pair of equations: \(r_1 = 2\) and \(r_2 = \sec \theta \).
Here we will use a table of values for each function, solving by quadrant. Recall that the period of \(\sec \theta\) is \(2\pi \).
Solution
For the first quadrant:
| \(\theta\) (angle) | 0 | \(\dfrac{\pi}{6}\) | \(\dfrac{\pi}{4}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{\pi}{2}\) |
|---|---|---|---|---|---|
| \(r_1\) (distance) | 2 | 2 | 2 | 2 | 2 |
| \(r_2\) | 1 | 1.15 | 1.4 | 2 | und |
For the second quadrant:
| \(\theta\) (angle) | \(\dfrac{2 \pi}{3}\) | \(\dfrac{3 \pi}{4}\) | \(\dfrac{5 \pi}{6}\) | \(\pi\) |
|---|---|---|---|---|
| \(r_1\) (distance) | 2 | 2 | 2 | 2 |
| \(r_2\) | -2 | -1.4 | -1.15 | -1 |
For the third quadrant:
| \(\theta\) (angle) | \(\dfrac{7 \pi}{6}\) | \(\dfrac{5 \pi}{4}\) | \(\dfrac{4 \pi}{3}\) | \(\dfrac{3 \pi}{2}\) |
|---|---|---|---|---|
| \(r_1\) (distance) | 2 | 2 | 2 | 2 |
| \(r_2\) | -1.15 | -1.4 | -2 | und |
For the fourth quadrant:
| \(\theta\) (angle) | \(\dfrac{5 \pi}{3}\) | \(\dfrac{7 \pi}{4}\) | \(\dfrac{11 \pi}{6}\) | \(2\pi\) |
|---|---|---|---|---|
| \(r_1\) (distance) | 2 | 2 | 2 | 2 |
| \(r_2\) | 2 | 1.4 | 1.15 | 1 |
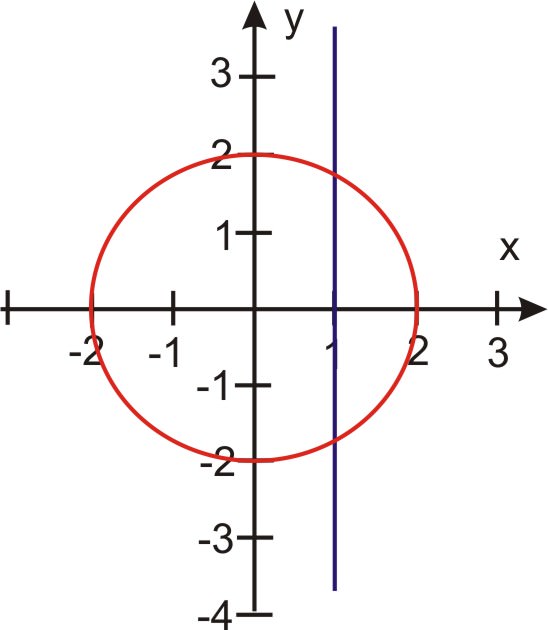
Note that the 3rd and 4th quadrant repeat 1st and 2nd quadrant values.
Observe in the table of values that \(\left(2, \dfrac{\pi}{3}\right)\) and \(\left(2, \dfrac{5 \pi}{3}\right)\) are the points of intersection. Look at the curves- the first equation yields a circle while the second yields a line. The maximum number of intersecting points for a line and a circle is 2. The two points have been found.
Find the point(s) of intersection for this pair of Polar equations: \(r = 2 + 4 \sin \theta\) and \(\theta = 60^{\circ}\).
Solution
The equation \(\theta = 60^{\circ}\) is a line making a \(60^{\circ}\) angle with the r axis.
Make a table of values for \(r = 2 + 4 \sin \theta\)
For the first quadrant:
| \(\theta\) (angle) | 0 | 30 | 45 | 60 | 90 |
|---|---|---|---|---|---|
| R (distance) | 2 | 4 | 4.83 | 5.46 | 6 |
For the second quadrant:
| \(\theta\) (angle) | 120 | 135 | 150 | 180 |
|---|---|---|---|---|
| R (distance) | 5.46 | 4.83 | 4 | 2 |
For the third quadrant:
| \(\theta\) (angle) | 210 | 225 | 240 | 270 |
|---|---|---|---|---|
| R (distance) | 0 | -.83 | -1.46 | -2 |
For the fourth quadrant:
| \(\theta\) (angle) | 300 | 315 | 330 | 360 |
|---|---|---|---|---|
| R (distance) | -1.46 | -.83 | 0 | 2 |
Notice there are two solutions in the table., \((60, 5.46)\) and \((240, -1.46) = (60, 1.46)\). Recall that when \(r < 0\), you plot a point \((r, \theta )\), by rotating \(180^{\circ}\) (or \(\pi\)).
Finally, we need to check the pole: \(r = 2 + 4 \sin \theta \) passes through the pole for \(\theta = 330^{\circ}\), and \(\theta = 60^{\circ}\) also passes through the pole. Thus, the third point of intersection is \((0, 0)\).
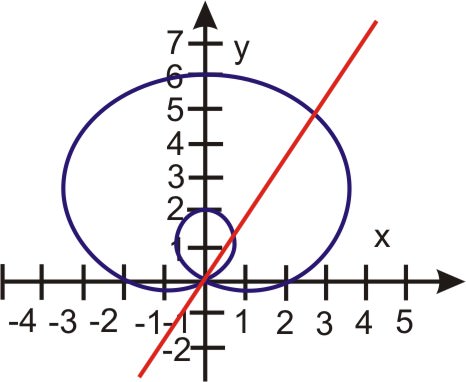
Find the point(s) of intersection for this pair of Polar equations: \(r_1 = 2 \cos \theta\) and \(r_2 = 1\).
Solution
Make a table:
For the first quadrant:
| \(\theta\) (angle) | 0 | \(\dfrac{\pi}{6}\) | \(\dfrac{\pi}{4}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{\pi}{2}\) |
|---|---|---|---|---|---|
| \(r_1\) (distance) | 2 | \(\sqrt{3}\) | \(\sqrt{2}\) | 1 | 0 |
| \(r_2\) | 1 | 1 | 1 | 1 | 1 |
For the second quadrant:
| \(\theta\) (angle) | \(\dfrac{2 \pi}{3}\) | \(\dfrac{3 \pi}{4}\) | \(\dfrac{5 \pi}{6}\) | \(\pi\) |
|---|---|---|---|---|
| \(r_1\) (distance) | -1 | \(−\sqrt{2}\) | \(−\sqrt{3}\) | -2 |
| \(r_2\) | 1 | 1 | 1 | 1 |
For the third quadrant:
| \(\theta\) (angle) | \(\dfrac{7 \pi}{6}\) | \(\dfrac{5 \pi}{4}\) | \(\dfrac{4 \pi}{3}\) | \(\dfrac{3 \pi}{2}\) |
|---|---|---|---|---|
| \(r_1\) (distance) | \(−\sqrt{3}\) | \(−\sqrt{2}\) | -1 | 0 |
| \(r_2\) | 1 | 1 | 1 | 1 |
For the fourth quadrant:
| \(\theta\) (angle) | \(\dfrac{5 \pi}{3}\) | \(\dfrac{7 \pi}{4}\) | \(\dfrac{11 \pi}{6}\) | \(2\pi\) |
|---|---|---|---|---|
| \(r_1\) (distance) | 1 | \(\sqrt{2}\) | \(\sqrt{3}\) | 2 |
| \(r_2\) | 1 | 1 | 1 | 1 |
So the unique solutions are at \(\theta =\dfrac{\pi }{3}, \dfrac{4\pi }{3}\). There are also two repeated solutions in this set (can you find them?).
Here is a graph showing the two solutions:
Review
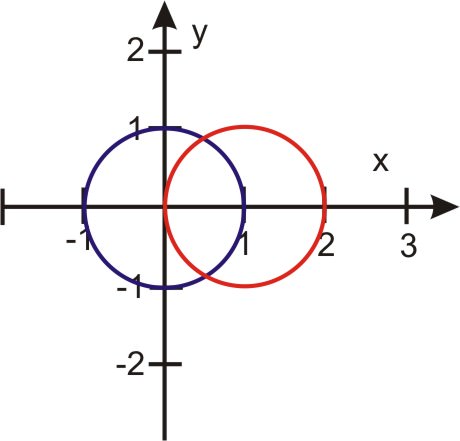
The graphs of \(r=1\) and \(r=2\cos \theta \) are shown below.
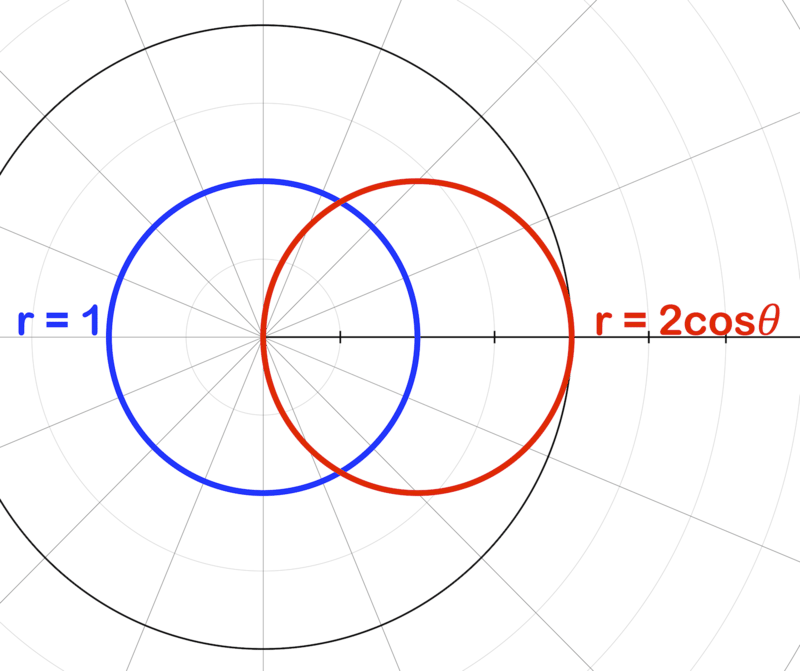
- How many times do they intersect?
- In which quadrants do they intersect?
- At what points do the intersections occur?
Based on the image below and the following information: the intersection of the graphs of \(r=\cos \theta \) and \(r=1−\cos \theta\)
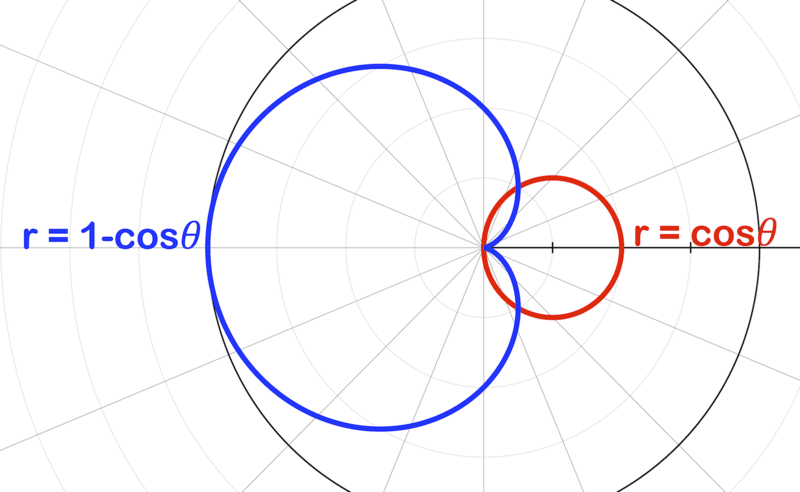
- Identify how many times they intersect?
- At what points do the intersections occur?
Find the points of intersection of the following pairs of curves.
- \(r=2 ; r=2\cos \theta\)
- \(r=\sin 2\theta ; r=2\sin \theta\)
- \(r=2+2\sin \theta ; r=2−2\cos \theta\)
- \(r=3\cos \theta ; r=2−\cos \theta\)
Find the point(s) of intersection for each system of equations. Graph to verify your solution.
- \(r_1 =csc\theta ; r_2 =2\sin \theta\)
- \(r_1 =\cos \theta ; r_2 =1+\sin \theta\)
- \(r_1 =\sin \theta ; r_2 =\sin 2\theta\)
- \(r_1 =−4\sin \theta ; r_2 =−4\cos \theta\)
- \(r_1 =1−2\sin \theta ; r_2 =\sqrt{9 \cos (\theta )}\)
- \(r_1 =1−\cos \theta ; r_2 =4\cos (3\theta )\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 4.3.
Vocabulary
| Term | Definition |
|---|---|
| Conic | Conic sections are those curves that can be created by the intersection of a double cone and a plane. They include circles, ellipses, parabolas, and hyperbolas. |
| Points of intersection | Points of intersection are locations where two different equations have the same solutions. |
| polar coordinates | Polar coordinates describe locations on a grid using the polar coordinate system. The location of each point is determined by its distance from the pole and its angle with respect to the polar axis. |
| pole | The pole is the center point on a polar graph. |
| quadrant | A quadrant is one-fourth of the coordinate plane. The four quadrants are numbered using Roman Numerals I, II, III, and IV, starting in the top-right, and increasing counter-clockwise. |
Additional Resources
Video: Example: Finding Points of Intersection on a Polar Graph
Practice: Systems of Polar Equations

