5.3.8: Geometry of Complex Roots
- Page ID
- 14914
Roots equally spaced around circles.
You've just finished a problem where you needed to solve the equation:
\(x^4=16\)
After solving for the roots, which were \(2,\; −2,\; 2i,\; −2i\) your instructor asks you to plot them on the complex plane.
Can you accomplish this?
It's always good to get an intuitive feel for values by plotting them. This tendency extends into the complex numbers as well.
The five roots of the equation \(x^5−32=0\) involve one real root and four complex ones. Let's take a look at a plot of these roots in the complex plane.
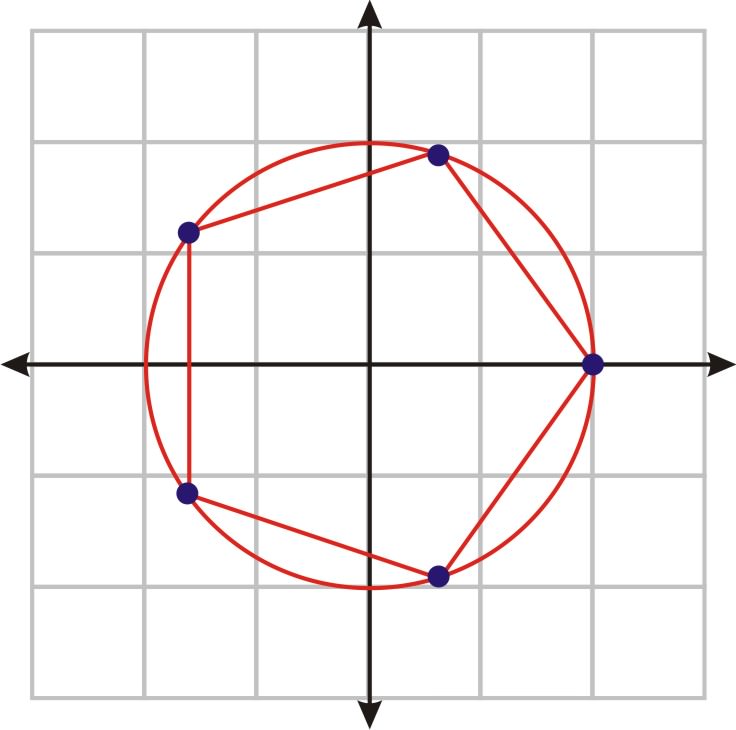
The \(n^{th}\) roots of a complex number, when graphed on the complex plane, are equally spaced around a circle. So, instead of having all the roots, all that is necessary to graph the roots is one of them and the radius of the circle. For this particular example, the roots are \(\dfrac{2\pi }{5}\) or \(72^{\circ} \) apart. This goes along with what we know about regular pentagons. The roots are \(\dfrac{2\pi }{n}\) degrees apart.
Let's take a look at some problems involving the geometry of complex roots.
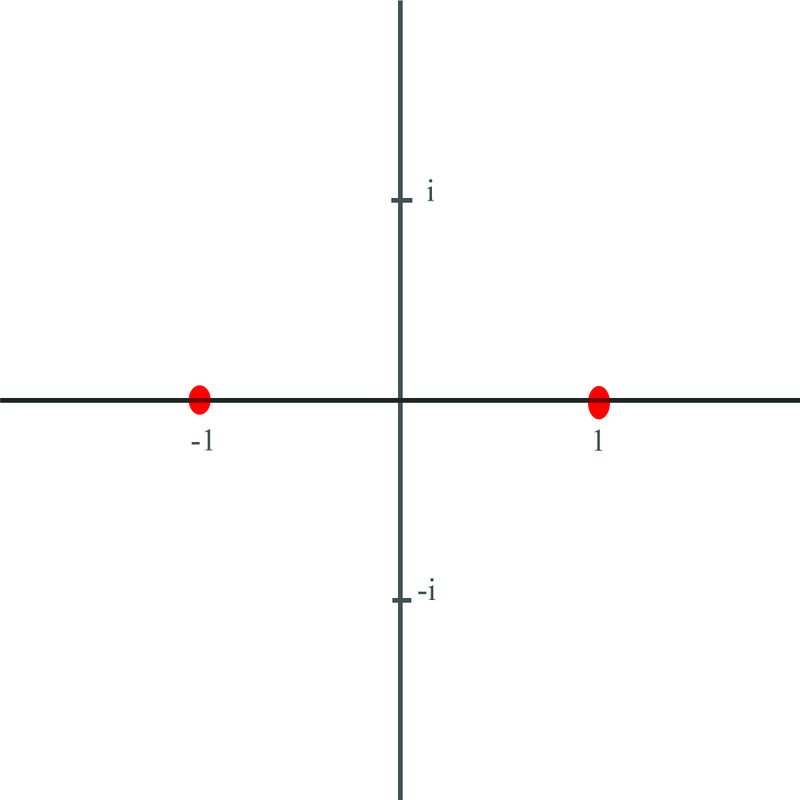
1. Calculate the two roots for \(x^2=1\) and represent them graphically.
\(\begin{aligned}
x^{2}=1 & \\
r &=\sqrt{x^{2}+y^{2}} \\
r &=\sqrt{(1)^{2}+(0)^{2}} \\
r &=1 \\
& \theta=\tan ^{-1}\left(\frac{0}{1}\right)=0
\end{aligned}\)
Write an expression for determining the two roots of \(1=1+0i\)
\(\begin{aligned}
1^{1/2} &=\left[1(\cos (0+2 \pi k)+i \sin (0+2 \pi k)\right]^{1/2}\\
&=1\left(\cos \frac{2 \pi k}{2}+i \sin \frac{2 \pi k}{2}\right) k=0,1 \\
x_{1} &=1\left(\cos \frac{0}{2}+i \sin \frac{0}{2}\right) \rightarrow 1(\cos 0+i \sin 0)=1 \quad \text { for } k=0 \\
x_{2} &=1\left(\cos \frac{2 \pi}{2}+i \sin \frac{2 \pi}{2}\right)=-1 \quad \text { for } k=1
\end{aligned}\)
These roots are plotted here:
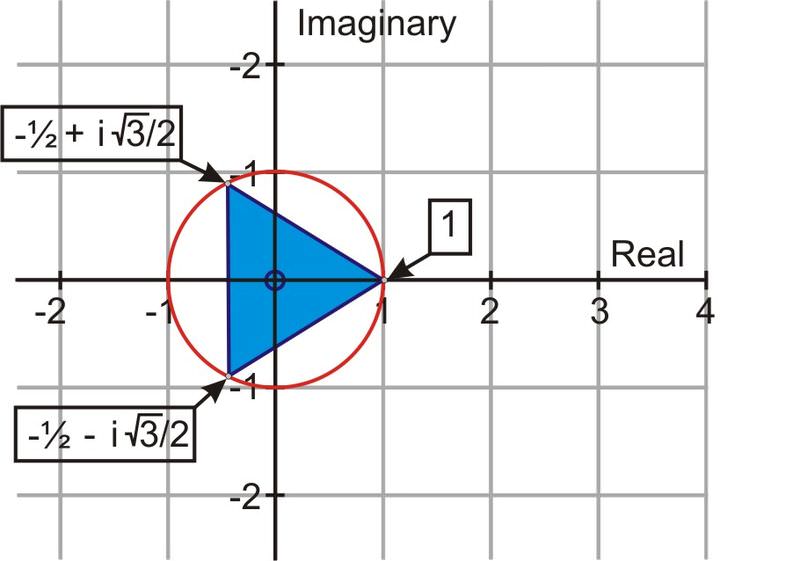
2. Calculate the three roots for \(x^3=1\) and represent them graphically.
In standard form, \(1=1+0i r=1\) and \(\theta =0\). The polar form is \(1+0i=1[\cos(0+2\pi k)+i\sin(0+2\pi k)]\). The expression for determining the cube roots of 1+0i is:
\((1+0i)^{1/3}=1^{1/3}\left(\cos \dfrac{0+2\pi k}{3}+i \sin \dfrac{0+2\pi k}{3}\right)\)
When \(k=0\), \(k=1\) and \(k=2\) the three cube roots of 1 are \(1,\; −\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2},\;−\dfrac{1}{2}−i\dfrac{\sqrt{3}}{2}\). When these three roots are represented graphically, the three points, on the circle with a radius of 1 (the cubed root of 1 is 1), form a triangle.
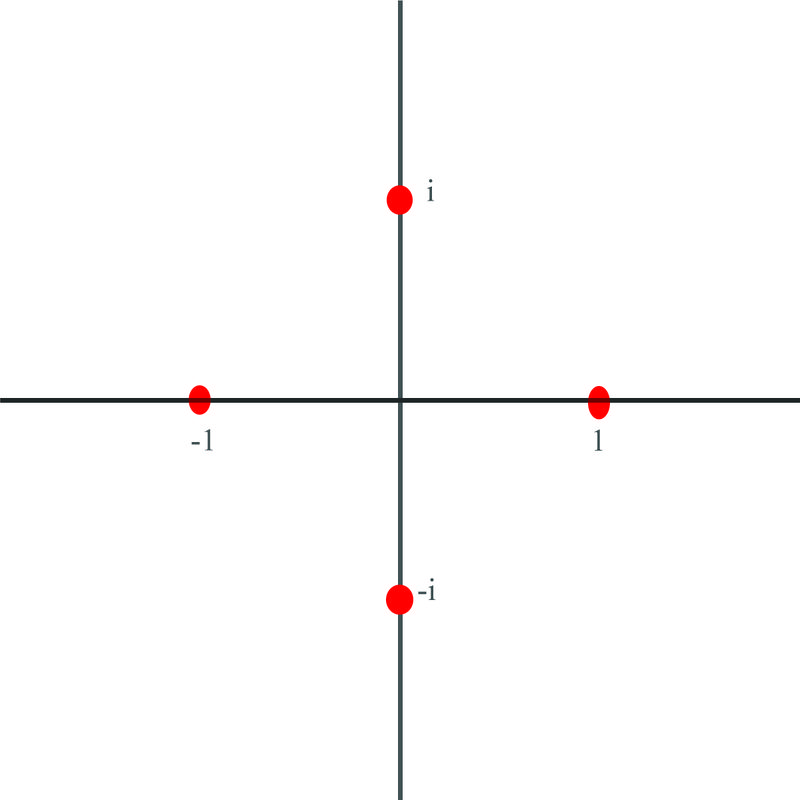
3. Calculate the four roots for \(x^4=1\) and represent them graphically
\(\begin{aligned}
x^{4}&=1 \\
r &=\sqrt{x^{2}+y^{2}} \\
r &=\sqrt{(1)^{2}+(0)^{2}} \\
r &=1 \\
& \theta=\tan ^{-1}\left(\frac{0}{1}\right)=0
\end{aligned}\)
Write an expression for determining the cube roots of \(1=1+0i\)
\(\begin{array}{rlr}
1^{\frac{1}{4}} & =\left[1(\cos (0+2 \pi k)+i \sin (0+2 \pi k)\right]^{1/4}& \\
& =1\left(\cos \frac{2 \pi k}{4}+i \sin \frac{2 \pi k}{4}\right) k=0,1,2,3 & \\
x_{1} & =1\left(\cos \frac{0}{4}+i \sin \frac{0}{4}\right) \rightarrow 3(\cos 0+i \sin 0)=1 & & \text { for } k=0 \\
x_{2} & =1\left(\cos \frac{2 \pi}{4}+i \sin \frac{2 \pi}{4}\right)=0+i=i & & \text { for } k=1 \\
x_{3} & =1\left(\cos \frac{4 \pi}{4}+i \sin \frac{4 \pi}{4}\right)=-1-0 i=-1 & & \text { for } k=2 \\
x_{4} & =1\left(\cos \frac{6 \pi}{4}+i \sin \frac{6 \pi}{4}\right)=0-i=-i & & \text { for } k=3
\end{array}\)
These roots are plotted here:
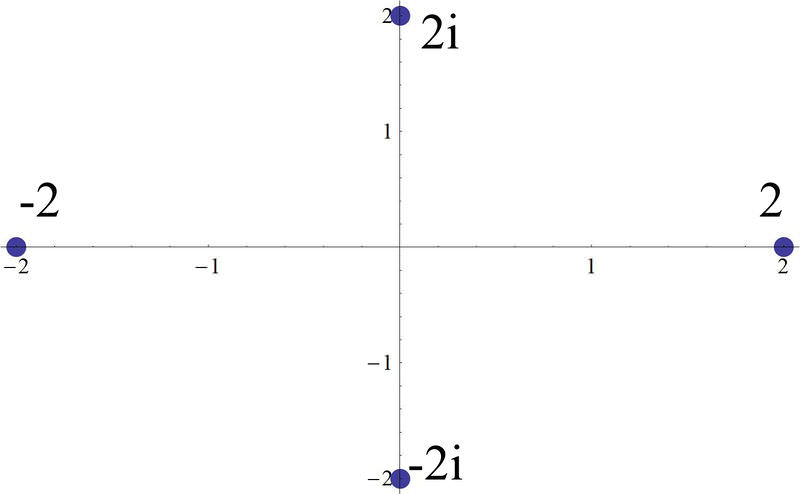
Earlier, you were asked to plot \(2,\;−2,\;2i,\;−2i\) on a plane.
Solution
You can see a plot of these roots here. Notice, as mentioned before, that the roots are placed equidistant around a circle that could be drawn in the plane with a radius of two.
In the examples above, you saw the complex roots determined for a number of different polynomial orders, such as \(x^2,\; x^3,\; x^4\). What conclusion can you draw about the number of complex roots there are in relation to the order of the polynomial being solved?
Solution
You can conclude that the total number of roots is the same as the order of the polynomial under consideration. For example, \(x^2\) will have 2 roots, while \(x^3\) will have 3 roots, etc.
What is the spacing in polar coordinates between the roots of the polynomial \(x^6=12\)?
Solution
Since there are six total roots, and all of the roots are equally spaced around a circle in the complex plane, there are \(\dfrac{360^{\circ} }{6}=60^{\circ} \) between roots.
Solve for the roots of the equation \(x^2−3x+5=0\) and plot them.
Solution
This equation can be solved using the familiar quadratic formula. Notice that previously we used quadratics that gave real solutions. However, there is no reason to limit the solution set to the real numbers, now that you know how to utilize complex numbers as well.
\(\begin{aligned}
x&=\frac{-(-3) \pm \sqrt{(-3)^{2}-(4)(1)(5)}}{(2)(1)} \\
&=\frac{3 \pm \sqrt{-11}}{2} \\
&=\frac{3 \pm i \sqrt{11}}{2} \\
&=\frac{3}{2} \pm \frac{i \sqrt{11}}{2}
\end{aligned}\)
A plot of these roots looks like this:
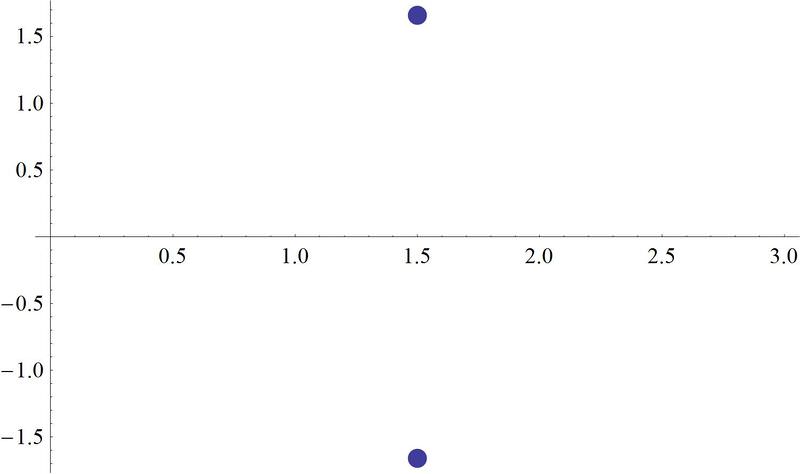
where the vertical axis is the imaginary number line.
Review
- How many roots does \(x^5=1\) have?
- Calculate the roots of \(x^5=1\) and represent them graphically.
- How many roots does \(x^8=1\) have?
- Calculate the roots of \(x^8=1\) and represent them graphically.
- How many roots does \(x^{10}=1\) have?
- Calculate the roots of \(x^{10}=1\) and represent them graphically.
- How many roots does \(x^4=16\) have?
- Calculate the roots of \(x^4=16\) and represent them graphically.
- How many roots does \(x^3=27\) have?
- Calculate the roots of \(x^3=27\) and represent them graphically.
- How do the solutions of the equation \(x^3=−1\) compare to the solutions of the equation \(x^3=1\)?
- Describe how to represent the roots of \(x^6=1\) graphically without first solving the equation.
- Describe how to represent the roots of \(x^{12}=1\) graphically without first solving the equation.
- Describe how to represent the roots of \(x^4=81\) graphically without first solving the equation.
- Describe how to represent the roots of \(x^8=256\) graphically without first solving the equation.
Review (Answers)
To see the Review answers, open this PDF file and look for section 6.15.

