3.2: Assembling the Periodic Table
- Page ID
- 5653
Overview
Following the Big Bang, the only atomic elements that existed in the early universe were hydrogen, helium and lithium. All other elements in the Periodic Table were formed later in the cores of stars. Since we need those other elements to form planets and life, we consider the process of star and planet formation and nucleosynthesis in this chapter.
Nucleosynthesis
Nucleosynthesis is the process of synthesizing heavier elements from lighter elements. In the Sun and other stars, the most common atom is hydrogen. It is possible for hydrogen nuclei (protons) overcome the strong electrostatic repulsive forces because of the enormous temperature and pressure in the core of a star. The energy output of the Sun is 3.8 x 1026 Joules per second (the energy per second is the luminosity of the Sun). This energy comes from the fusion of hydrogen into helium in the core of the Sun.
H-fusion: the p-p chain
The exact pathway for nucleosynthesis is very temperature-dependent. In a star like the Sun (or less massive than the Sun), the process is proton-proton (or p-p) fusion and follows the steps outlined in the figure below.
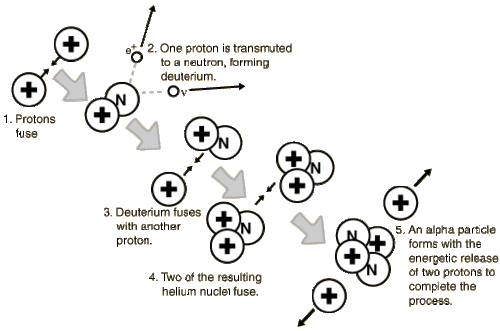
How many hydrogen nuclei are needed to produce a helium nucleus?
A few things to know.
First: Recall that the hydrogen nucleus is simply a proton, and the helium nucleus (also called an alpha particle) has two protons and two neutrons.
Second: protons and neutrons are not fundamental particles, they are comprised of a soup of quarks, anti-quarks, gluons - their nature, a fascinating tale of quantum mechanics, is being explored a particle accelerators like the Large Hadron Collider (LHC). Protons have two "Up" and one "Down" quark, while neutrons have one "Up" and two "Down" quarks. By using a bit of energy to transmute the spin of one "Up" quark, a proton can change into a neutron. This is a statistically rare process, but there are a lot of protons and a lot of energy in the core of the Sun.
Take a look at the Figure above to see how many protons (a.k.a. hydrogen nuclei) are needed to build one helium nucleus. Importantly, the mass of the helium nucleus is less than the mass of the 4 protons. That mass difference is converted into the energy that is radiated by the Sun.
In the first step of p-p nucleosynthesis, a small fraction of hydrogen transforms into deuterium (an isotope of hydrogen with a neutron added to the nucleus). This is the rate-limiting step in the p-p chain because the transformation of a proton into a neutron is statistically improbable. Once deuterium is created, the rest of the p-p pathway proceeds relatively quickly.
As hydrogen fusion occurs in the Sun, most of the mass of the hydrogen is converted into an "ash" of helium. However, there is a slight difference of 0.71% between the mass of 4 protons and the mass of a helium nucleus; this fraction of the original mass is converted into energy and the mass loss rate from the Sun, Δm, can be calculated with Einstein's famous equation:
\[E\,=\Delta mc^2 \qquad\,E\,=\,3.8\times 10^{26}\,Joules\qquad c\,=\,3\times\,10^8\,m\,s^2\]
The mass that is converted into energy every second is:
\(\Delta m\,=\frac{E}{c^2}\,4\times\,10^9\,kg\,=\,4.4\,\text{million tons}\)
Think about that... every second, 4.4 million tons (or 4.4 billion kg) of the mass of our Sun vanishes - it is transformed into energy that is radiated away. However, this only represents 0.71% of the mass of hydrogen that is converted into helium. How much hydrogen is being burned in the sun every second?
(m_H\,=\frac{4\times\,10^9\,kg}{0.0071}\,=\text{600 billion kg}\)
600 billion kg of hydrogen are used up by nucleosynthesis in the Sun every second. Should we feel nervous? How long can our Sun last if it is burning hydrogen at this rate?
The mass of the Sun is 2 x 1030 kilograms and 90% of the solar mass is hydrogen. If we take the naive view that the rate of fusion is constant and that 100% of the mass of the Sun is used in nucleosynthesis, how long would the Sun live before the hydrogen is gone?
\(\frac{2\times 10^{30}}{6\times 10^{11}}\,=\,3.3\times 10^{18} \text{seconds = 95 Gyr (95 Billion years)}\)
Of course, hydrogen fusion requires high temperatures and pressures that are only found in the core of the Sun, so the lifetime is actually shorter by about a factor of 10. But, you can sleep well tonight, knowing that even though the Sun is churning out an incredible amount of energy, there is still enough fuel for another ~5 billion years.
H-fusion: the CNO chain
Stars that are more massive than the Sun have more gravitational pressure in their cores and hotter temperatures. Massive stars that have trace amounts of carbon, nitrogen and oxygen (CNO) can take a more efficient path for synthesizing helium, using CNO as catalysts to form helium nuclei (figure below). The energy yield is higher and therefore more efficient: 26.72 MeV per helium nucleus instead of 25 MeV per helium nucleus with the p-p pathway.
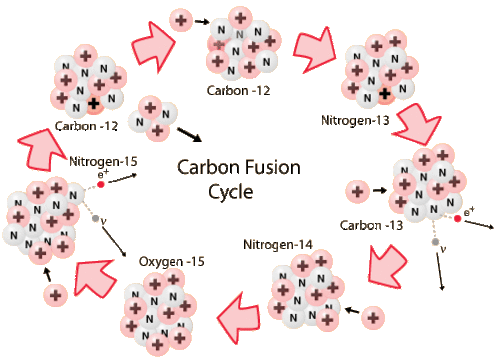
Stars that are more massive than the Sun will have higher temperatures in their cores. This allows them to use a more efficient pathway for H-fusion, using CNO as catalysts. The first stars to form after the Big Bang were more massive than stars today. Would those stars have experienced H-fusion through the CNO chain?
Manufacturing heavier elements
So, if hydrogen fusion is forming a helium "ash" core, how does that get us to carbon, oxygen, nitrogen, phosphorus, sulfur.... all the good stuff that we need for life? Stars on the main sequence only burn hydrogen in their cores. Elements with atomic masses greater than helium can only be formed after the star leaves the main sequence. After most of the hydrogen in the core has been fused to helium, hydrogen fusion slows down. This is a problem for the star because H-fusion was supporting the star against gravitational collapse. As the rate of H-fusion declines, gravity begins to win, and the core of the star collapses. This causes the pressure and temperature to increase. When the pressure and temperature are high enough, helium fusion in the core is initiated. During this gravitational collapse, the pressure and temperature of hydrogen gas in a shell surrounding the core "reignites" and begins forming helium.
The helium nucleus (a.k.a. alpha particle), with a mass number of four (2 protons, 2 neutrons) begins fusion reactions, forming carbon (mass number 12) though a "triple alpha" process. Adding another alpha particle to the nucleus of carbon yields an oxygen nucleus. For "low mass" stars (M ≤ a few M⊙) this is the end of nuclear fusion reactions. Low mass stars (like the Sun) do not form most of the elements that we need for life. For this, we need high mass stars.
Massive stars are rare with relatively short lifetimes (millions rather than billions of years). But, massive stars do all of the heavy lifting when it comes to manufacturing high atomic mass elements. Like their lower mass counterparts, massive stars burn hydrogen on the main sequence. But when hydrogen fusion ends, there is a rapid succession of fusion and collapse events. When the core depletes the element it is burning in the core, gravity squeezes the star and the next stage of core nuclear fusion along with shell burning of lighter elements begins. Close to the end of its life, the massive star has developed a stratified, onion skin structure with the heaviest elements in the core and surrounding shells of successively lighter elements. However, that fusion stops when iron is formed in the core. For elements with lower atomic mass than iron, fusion reactions are exothermic - they give off energy and support the star against gravity. Iron fusion is endothermic - energy is used in this reaction.
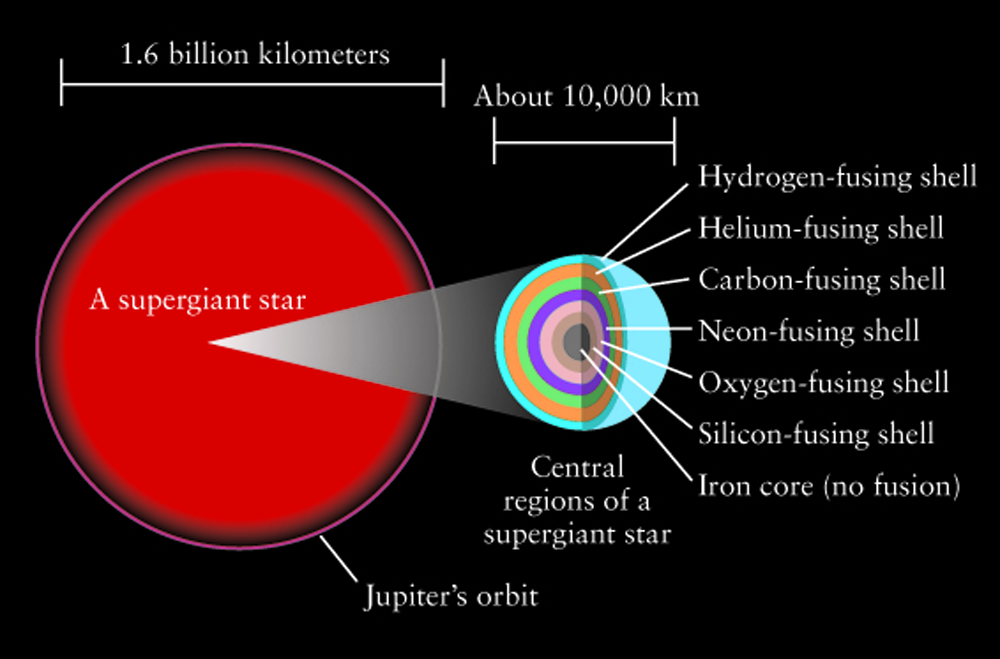
The next move belongs to gravity. Once the core collapse begins, the onion shells in the core mix, and the density increases. The outer layers of the star fall in, hit the high density core, and bounce off in a fierce supernova event that blows out about half of the material in the star. During the supernova, the shock waves generate high enough pressures to produce the heaviest elements in the Periodic Table. The final distribution of elements has some interesting structure. The addition of alpha particles favors production of even-numbered atomic mass elements and leaves behind an even-odd pattern in the logarithmic elemental abundances. There is an obvious iron peak in the elemental abundances with higher mass elements being increasingly rare.
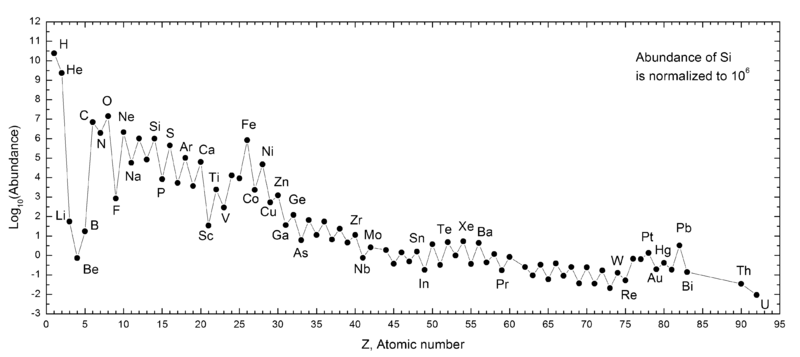
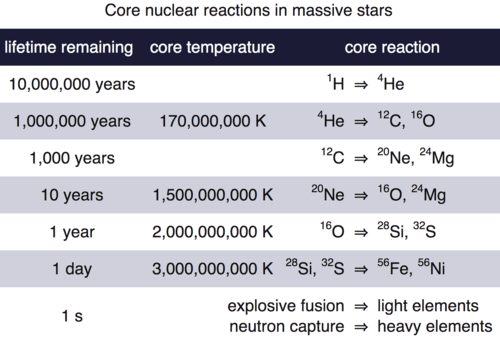
The Table below drives home the dramatic timescales for production of heavy elements. The high mass star spends 90% of its life on the main sequence forming helium. The next stages of nucleosynthesis are increasingly rapid and the formation of elements heavier than iron occur in a one-second flash of time.
Completing the Periodic Table of Elements
The sources for the ordered Table of Elements are summarized below. All of the hydrogen that exists today was formed in the Big Bang. Most of the helium today was also formed in the Big Bang. However, hydrogen fusion in the cores of stars produces helium and a small fraction of helium today is released during the explosive deaths of stars. The lithium atoms that exist today were formed by three processes: big bang nuclear fusion, the evolution of low mass stars, and cosmic ray fission (splitting) of heavier atoms. Beryllium and Boron are used up as fast as they form in the cores of stars. They are used as building blocks for heavier elements and never make it out of the core of a star. These light elements must be produced outside of stars by a process of spallation, where cosmic rays cleave heavier elements. Most of the heavy elements are formed during explosive evolution of stars and Type 1a supernovae.
A new process for manufacturing the heaviest atomic elements has recently been in the news. The Laser Interferometer Gravitational wave Observatory (LIGO) has registered tiny ripples in the space-time continuum when orbiting neutron stars or black holes undergo a collision. Orbiting neutron stars will radiate gravitational energy according to a prediction made by Einstein. As the binary stars lose energy, their orbits should decay until the two spiraling stellar remnants merge, triggering the release of a hypothesized gravitational wave. In August, 2017, a gravitational wave and the energetic optical counterpart of a neutron star merger was observed.
As the neutron stars smash together, some of the neutron material is liberated from the stars, losing their ultra-high density. A hot, expanding shell now contains some of the heaviest elements in the Periodic Table and these elements experience a brief flash of nuclear fusion, producing heavy elements like lead (Pb), platinum (Pt) and gold (Au). The coded Periodic Table summarizes the important contribution of rare earth elements from neutron stars mergers.

Galactic Chemical Enrichment
The universe began with a Big Bang. The first stars were only comprised of hydrogen and helium and they collected into initially small galaxies that grew by mergers. As stars ended their lives, they enriched the interstellar medium with higher atomic mass elements. The massive stars formed all of the elements with atomic masses greater than iron during supernova explosions in the last seconds of their lives. All of these heavy elements collected into giant molecular clouds that seeded the next generation of stars, enriched in metals (astronomers refer to all elements in the Periodic Table that are not hydrogen or helium as "metals"). The galaxies act as distribution centers, recycling the heavy elements from dying stars into the next generation of stars. Somewhere along the path to galactic chemical enrichment, protostellar disks had enough heavy elements to build planets.
Of course, in some sense, astronomers learned all of this "backwards." The stars closest to us were observed first and like the Sun, we could detect the presence of small quantities of metals. The table below shows the mass fraction and number fraction for the most common atoms (about 70 elements have been observed altogether) in the Sun. Later, we observed stars in our galaxy that were older and more metal poor. Naturally, we called the stars like our Sun "Population I" stars and the metal poor stars were "Population II" stars. One of the holy grails in astronomy is the search for "Population III" stars - the oldest stars in the universe.
|
Percentage of total number of atoms | Percentage of total mass |
| Hydrogen | 91.2 | 71.0 |
| Helium | 8.7 | 27.1 |
| Oxygen | 0.078 | 0.97 |
| Carbon | 0.043 | 0.4 |
| Nitrogen | 0.0088 | 0.096 |
| Silicon | 0.0045 | 0.099 |
| Magnesium | 0.0038 | 0.076 |
| Neon | 0.0035 | 0.058 |
| Iron | 0.0030 | 0.14 |
| Sulfur | 0.0015 | 0.04 |
Learning things backwards is common in science. We make observations and develop theories. In many cases, we are observing the end state of objects and we have to reconstruct the origin. That is one of the important ways that science works. So, when our understanding and scientific theories change, it is cause for celebration, not a reason to dismiss the value of science.

