7.4: The Transit Method
- Page ID
- 5637
By 1999, about a dozen planet candidates had been detected with the Doppler technique and most were similar to 51 Peg b, with \(m_{planet}\sin i\) of about one Jupiter mass and orbits of just a few days. Even the astronomers working with the Doppler method were deferential in calling these objects planet "candidates" in those early days because the true mass of the orbiting companion could not be determined with this detection technique.
However, astronomers knew that if these really were planets (and not face-on stellar binary systems), about one in ten of the short-period 51 Peg b type objects would have an orbit that was oriented so that the planet would "transit" or cross our line of site to the star. When that happens, the planet blocks some of the starlight for the few hours that it transits.
Measuring the brightness of stars is relatively straightforward, and each of the stars with 51 Peg b type objects was being monitored for a possible transit. While the Doppler technique cannot determine the inclination, the data do predict when a planet will transit if the inclination is viewed nearly edge-on. If a planet transits, we know that \(i \sim \,90^∘\) and therefore, \(\sin i\sim 1.0\). In this case, the Doppler measured mass is no longer just \(m_{pl}\sin i\), it is the total, true mass of the planet.

The figure above illustrates what is happening. During a transit the planet passes in front of the star (top animation) and as this happens the brightness of the star decreases (bottom animation). We do not actually have pictures like the top animation because stars are point sources of light, not resolved objects. The data that we have is the time series photometry (brightness measurements) depicted in the lower animation that show a regular and periodic decrease in the brightness of the star at precisely the putative time time (predicted by the Doppler velocity measurements). Because we cannot resolve the image of the planet (or the star) this is still an indirect detection technique. However, even astronomers sometimes take some poetic license here and say that we are seeing the shadow (or the silhouette) of the planet.
There is only one case where we can resolve the physical extent of star, and that is for our Sun. If the Earth is in the right position on our orbit around the Sun, we can see the inner planets, Mercury and Venus, transiting the Sun. This fortuitous alignment happens about 13 times a century for Mercury and fewer than 2 times per century for Venus. The video below shows the transit of Venus, seen from Trondheim, Norway in June 2004. You will have to wait until Dec 10, 2117 to see the next transit of Venus. Can you estimate the transit depth for Venus crossing the Sun?
The first transiting exoplanet
HD 209458 b was the first star where astronomers observed a transiting exoplanet. The planet had a mass similar to Jupiter with a short orbital period of just a few days, and was independently detected by two teams using the Doppler method in the summer of 1999. HD 209458 b was the twelfth example of a 51 Peg b analog -- recall that about one in ten close-in planets was expected to transit -- and the planet hunters were anxiously awaiting the validation of "planet" status that a transit would bring.
In August and September 1999, the team led by Harvard graduate student David Charbonneau and Dr. Tim Brown, observed a transit at the time predicted by the Doppler velocity data. Their published data is shown in the Figure below. The ground based photometry is good enough that you can unambiguously see the transit event, but the scatter in the published relative flux over time reflects measurement errors from atmospheric scintillation - the twinkling effect on starlight caused by differences in temperature and pressure in different layers of the atmosphere. The team phase-folded the photometric data at one orbital period to strengthen the fidelity of the repeating signal was able to reduce their errors to 0.015%. This precision is impressive, but not high enough to detect a transiting planet like the Earth with a radius that is one tenth of Jupiter. A second team, led by Greg Henry measured a partial transit in November of that same year and the two discovery papers were published back-to-back in the Astrophysical Journal.

The depth of the transit tells us about the relative size of the planet and star. Imagine a planet that is large enough to completely cover (eclipse) the star during transit. In this extreme case, the brightness of the star would drop to zero. However, the typical case is that planet is much smaller than the star and in this case, the brightness of the star decreases by the ratio:
\[\frac{\Delta B}{B}\,=\,\frac{\text{cross sectional area of planet}}{\text{cross sectional area of star}}\,=\,\left(\frac{\pi r_{planet}}{\pi R_{\ast}}\right)^2\,=\,\left(\frac{r_{planet}}{R_{\ast}}\right)^2\]
Equation \(\PageIndex{1}\) says that the fractional change in brightness of the star is proportional to the radius of the planet to the star. We measure the brightness of the star without a transit and the decreased brightness during transit. So, if we know the radius of the star, we can solve this equation to derive the radius of a planet that we cannot even see. Science is amazing!
In our everyday lives, we have a lot of experience with what artists call perspective. Objects that are closer to us look larger than objects that are farther away. This sometimes lead to an incorrect intuition that transit depth is related to the star-planet separation since the more distant planet are "closer" to us. However, the incredible distances to the stars that we observe mean that the difference in star-planet distances within a given planetary system are negligible.
Transit Probability
Do all planets have an equal probability of transiting, or do some planets have a higher transit probability?
What factors might improve the chances that a planet will transit?
Transit probability
The transit probability depends on the serendipitous tilt, or inclination, of the orbital plane of the planets. If the planetary system is viewed "face-on" (by definition, this inclination angle is zero) then the planets will not transit. If the planetary system is exactly "edge-on" (in this case, the inclination angle is 90 degrees) then the planet will always transit. But what is the probability that a planet will transit if the inclination of the orbital plane is somewhere in between these two extremes? For these cases, the transit probability depends on the radius of the star and the distance between the star and the planet. The transit probability is derived from this geometry and expresses a simple dependency between stellar radius, R, and the star-planet distance, a, in the simple form:
\[P(transit)\,=\frac{R}{a}\]
Equation \(\PageIndex{2}\) captures the idea that larger stars present a bigger target for prospective transits (although the transit depth will be shallower and may be harder to detect than with smaller stars). Likewise planets that are closer to the star are more likely to transit.
If one planet transits its host star, will all of the other planets transit, too? Not necessarily. As figure \(\PageIndex{3}\) shows, it is more probable that the inner planets will transit. A more distant planet in the system could avoid transiting even if the system is perfectly co-planar.

Use the NAAP transit simulator (download from NAAP and install on your computer, then open the Exoplanet Transit Simulator) to understand how transiting exoplanets are detected with time series photometric data. Set up the simulator using the settings listed below:
- Familiarize yourself with the input widgets in the bottom three frames of the Transit Simulator window.
- Set the planet properties as shown: a 1 Mjup planet with a radius of 1 Rjup orbiting at 1 AU with zero eccentricity.
- Set the mass of the star to be equal to the mass of the Sun.
- Keep the system orientation with an edge-on inclination of 90 degrees with a longitude of zero.
- In the output window, toggle on the theoretical curve and the simulated measurements. Select "noise" in the data of 0.00020, typical errors in the Kepler data.
- Use the sliders to observe the impact on the data when the noise is increased and the number of observations is 10 or 100.
- Check to see how the mass of the star affects the strength of the transit signal (notice that the numbers on the y-axis will change). A lower mass star is smaller and fractionally more light is blocked out than for a high mass star with a large radius.
- The Earth has a mass that is 0.0032 times the mass of Jupiter and a radius that is about 0.1 times the radius of Jupiter. Change the planet mass and radius in the simulator to these value. Notice that the real change in the transit signal occurs when the radius, not the mass, is changed. Is there any way of convincingly detecting an Earth analog (Earth-size planet at 1 AU) around a solar mass star with the precision of the 0.0002? What precision do you need to be able to convincingly see the transit dip?
The Kepler Mission
A decade before the first exoplanet was discovered, William Borucki, a scientist at NASA Ames Research Center in Mountainview CA, wrote a paper "The Photometric Method of Detecting Other Planetary Systems" (Borucki & Summers 1984) where he made the case for a space mission to detect planets orbiting other stars using the transit technique. It took more than twenty years of advocacy, but Borucki's persistence paid off. The first exoplanets were discovered in the mid-1990's heating up interest and after the first ground-based transit discovery in 2000, the exoplanet community rallied behind Bill Borucki's plan.
The first question in deciding whether to go forward with a space mission is: can this be done from the ground? If so, then the mission is a no-go. The justification for the space-based Kepler transit mission was the need to reach higher precision. Ground-based transit surveys could only detect 1% (0.01) changes in the brightness. The important limitations to the precision of ground-based photometry (brightness measurement) blurring from the Earth's atmosphere and the limited number of dark nighttime hours when the telescopes point away from the Sun. From space, the atmospheric blurring is limited and the telescope can always point away from the Sun. The higher photometric precision was demonstrated by the Hubble Space Telescope, which measures 0.1% (0.001) changes in brightness. However, a special purpose telescope was really needed that could reach even higher precision with continuous monitoring of stars.
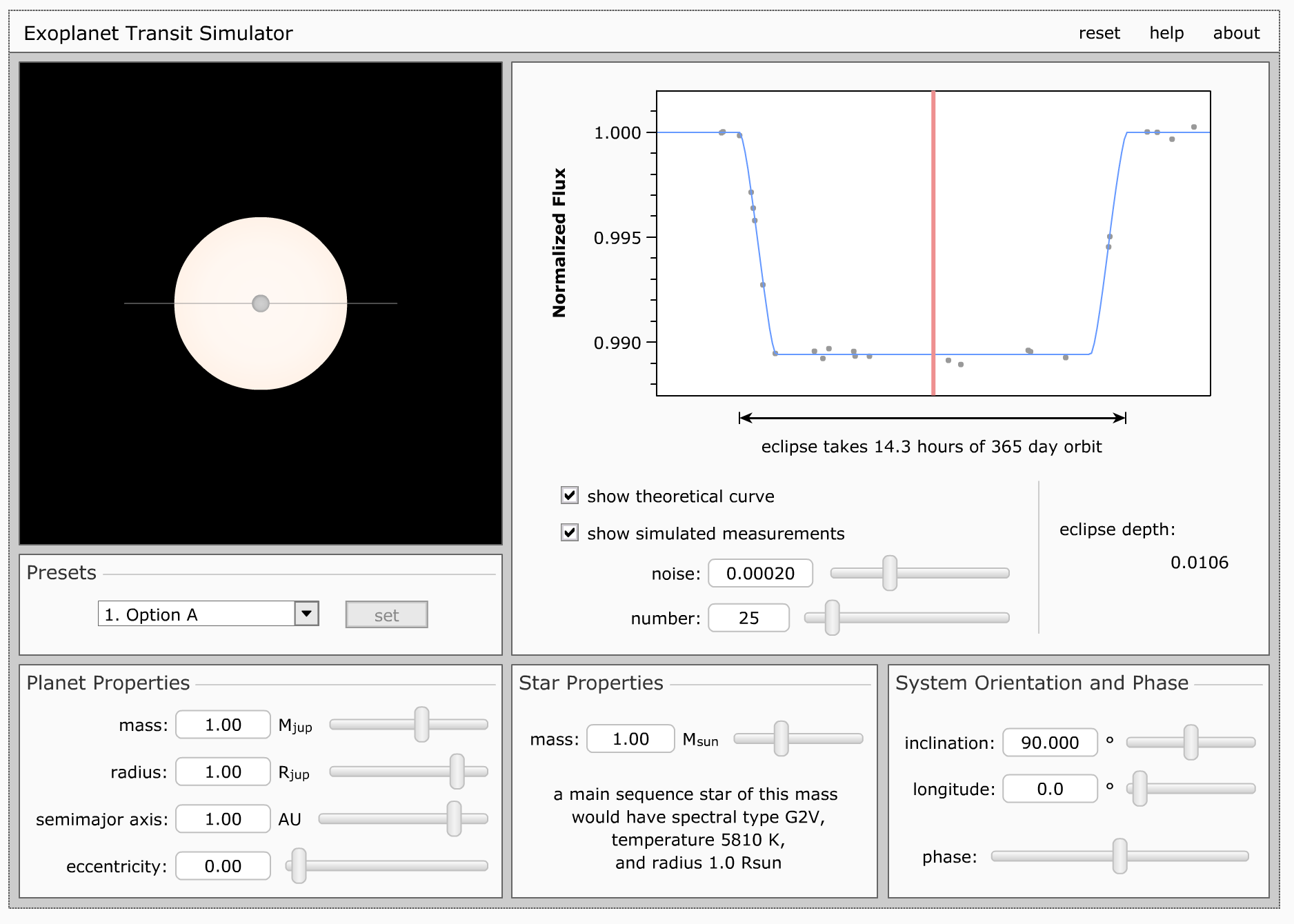
In 2009, NASA launched the Kepler Mission, which measures 0.01\% or (0.0001) changes in the brightness of the host star. The figure below shows that Kepler was remarkably successful in detecting a range of exoplanets with radii down to a couple times the radius of Earth.
The specific science goal for Kepler was to determine the occurrence rate of Earth-sized planets. The HAT-P-7 light curve below compares a light curve from a ground-based transit survey for the planet HAT-P-7b with data from the Kepler space mission. What a difference the higher precision made!

In 2011, the first rocky planet was discovered with the Kepler mission. The phase folded transit light curve from the original publication is shown in the figure below. The lead author on the discovery paper, Natalie Batalha, was also the Deputy Scientist for the space mission and her collaborative leadership style helped to make the NASA mission an incredible success. You can participate in the hunt for transiting planets in the Kepler data on the Zooniverse Planet Hunters website.


Multi-planet Transiting Systems
So far, we've only considered cases where there is just one transiting planet. In our solar system, the planets are nearly co-planar. What if there is more than one transiting planet in the time series light curve data? Would we be able to disentangle the different signals? If the planets are different sizes, then the transit depths will also differ. A second important parameter is the orbital period. Kepler's third law says that the orbital period is related to the semi-major axis of the orbit so that more distant planets have longer period orbits. With longer period orbits, the time interval between transits is also longer. So there are two important pieces of information that go into a model of a transiting system: the spacing between transits (i.e., the orbital period) and the depth of the transits.
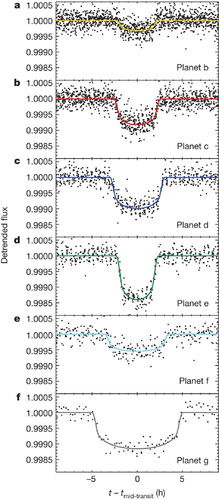
A good example of what data looks like for a system with more than one planet is shown in the figure below. The six planets in this system all orbit closer than the distance to Mercury in our solar system.

After detrending the light curve to remove instrumental errors in the photometry, transits of the individual planets are phase-folded and shown below.
Think about it...
Students will be modeling the dynamical interactions of Kepler multi-planet systems with the Yale Orbital Simulator Interface. Do you think that there are strong gravitational interactions between the planets in the Kepler-11 system that could drive the system to become unstable?

