1.1.4: Zeroes and Intercepts

Zeroes and Intercepts of Functions

An intercept in mathematics is where a function crosses the x or y axis. What are the intercepts of this function?

[Figure1]

---

X and Y Intercepts

The first type of intercept you may have learned is the y-intercept when you learned the slope intercept form of a line: y=mx+b. A y-intercept is the unique point where a function crosses the y axis. It can be found algebraically by setting x=0 and solving for y.

x-intercepts are where functions cross the x axis and where the height of the function is zero. They are also called roots, solutions and zeroes of a function. They are found algebraically by setting y=0 and solving for x. Watch the videos below for practice:

---

Examples

Example 1

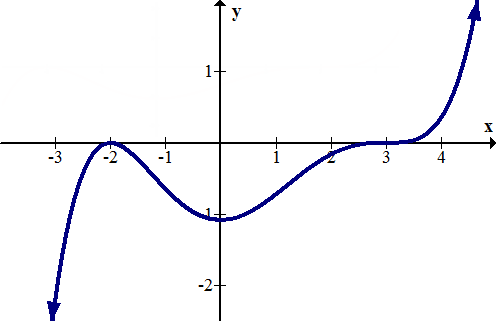
Earlier, you were asked what the intercepts of the graph below are.

[Figure2]

Solution

Graphically the function has zeroes at -2 and 3 with a y intercept at about -1.1.

Note: In order for a function to pass the vertical line test, it must only have one y-intercept, but it may have multiple x-intercepts.

Example 2

What are the zeroes and y-intercepts of the parabola y=x²−2x−3?

Using a graph:

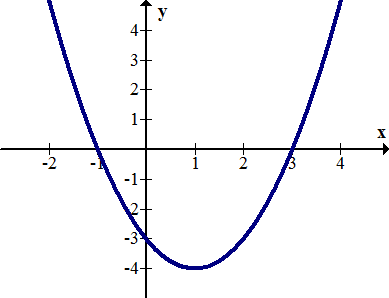[Figure3]

Solution

The zeroes are at (-1, 0) and (3, 0). The y-intercept is at (0, -3).

Using Algebra:

Substitute 0 for y to find zeroes.

0=x²−2x−3=(x−3)(x+1)

y=0,x=3,−1

Substitute 0 for x to find the y-intercept.

y=(0)²−2(0)−3=−3

x=0,y=−3

Example 3

Identify the zeroes and y-intercepts for the sine function.

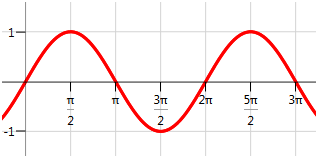[Figure4]

Solution

The y-intercept is (0, 0). There are four zeroes visible on this portion of the graph. One thing you know about the sine graph is that it is periodic and repeats forever in both directions. In order to capture every x-intercept, you must identify a pattern instead of trying to write out every single one.

The visible x-intercepts are 0,π,2π,3π. The pattern is that there is an x-intercept every multiple of π including negative multiples. In order to describe all of these values you should write:

The x-intercepts are ±nπ where n is an integer {0,±1,±2,…}.

Example 4

Identify the intercepts and zeroes of the function: \(\ f(x)=\frac{1}{100}(x-3)^{3}(x+2)^{2}\)

Solution

To find the y-intercept, substitute 0 for x:

\(\ y=\frac{1}{100}(0-3)^{3}(0+2)^{2}=\frac{1}{100}(-27)(4)=-\frac{108}{100}=-1.08\)

To find the x-intercepts, substitute 0 for y:

\(\ 0=\frac{1}{100}(x-3)^{3}(x+2)^{2}\)

x=3,−2

Thus the y-intercept is (0, -1.08) and the x-intercepts are (3, 0) and (-2, 0).

Example 5

Determine the intercepts of the following function graphically.

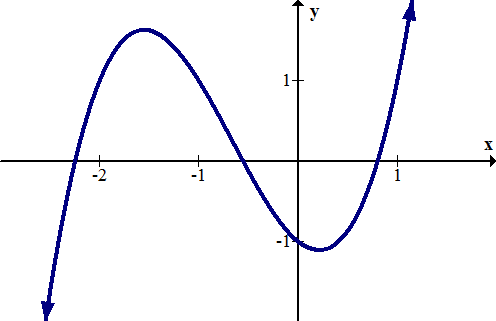[Figure5]

Solution

The y-intercept is approximately (0, -1). The x-intercepts are approximately (-2.3, 0), (-0.4, 0) and (0.7, 0). When finding values graphically, answers are always approximate. Exact answers need to be found analytically.

---

Review

1. Determine the zeroes and y-intercept of the following function using algebra:

f(x)=(x+1)³(x−4)

2. Determine the roots and y-intercept of the following function using algebra or a graph:

g(x)=x⁴−2x³−7x²+20x−12

3. Determine the intercepts of the following function graphically:

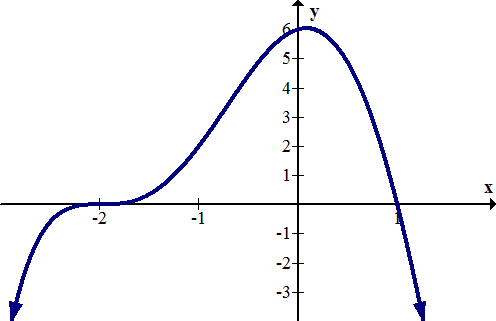[Figure6]

Find the intercepts for each of the following functions.

4. y=x²

5. y=x³

6. y=ln(x)

7. y=\(\ \frac{1}{x}\)

8. y=e^x

9. y=\(\ \sqrt{x}\)

10. Are there any functions without a y-intercept? Explain.

11. Are there any functions without an x-intercept? Explain.

12. Explain why it makes sense that an x-intercept of a function is also called a “zero” of the function.

Determine the intercepts of the following functions using algebra or a graph.

13. h(x)=x³−6x²+3x+10

14. j(x)=x²−6x−7

15. k(x)=4x⁴−20x³−3x²+14x+5

---

Review (Answers)

To see the Review answers, open this PDF file and look for section 1.8.

---

Vocabulary

Term	Definition
Intercept	The intercepts of a curve are the locations where the curve intersects the x and y axes. An x intercept is a point at which the curve intersects the x-axis. A y intercept is a point at which the curve intersects the y-axis.
Intercepts	The intercepts of a curve are the locations where the curve intersects the x and y axes. An x intercept is a point at which the curve intersects the x-axis. A y intercept is a point at which the curve intersects the y-axis.
Roots	The roots of a function are the values of x that make y equal to zero.
Vertical Line Test	The vertical line test says that if a vertical line drawn anywhere through the graph of a relation intersects the relation in more than one location, then the relation is not a function.
Zeroes	The zeroes of a function f(x) are the values of x that cause f(x) to be equal to zero.

---

Image Attributions

1. [Figure 1]
   Credit: CK-12 Foundation
   License: CC BY-SA
2. [Figure 2]
   Credit: CK-12 Foundation
   License: CC BY-SA
3. [Figure 3]
   Credit: CK-12 Foundation
   License: CC BY-SA
4. [Figure 4]
   Credit: CK-12 Foundation
   License: CC BY-SA
5. [Figure 5]
   Credit: CK-12 Foundation
   License: CC BY-SA
6. [Figure 6]
   Credit: CK-12 Foundation
   License: CC BY-SA