5.3.10: DeMoivre's Theorem and nth Roots
- Page ID
- 14910
Raise complex numbers to powers or find their roots.
You know how to multiply two complex numbers together and you’ve seen the advantages of using trigonometric polar form, especially when multiplying more than two complex numbers at the same time. Because raising a number to a whole number power is repeated multiplication, you also know how to raise a complex number to a whole number power.
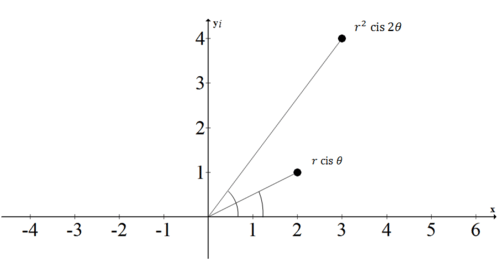
What is a geometric interpretation of squaring a complex number?
Recall that if \(z_1=r_1\cdot \; cis \; \theta_1\) and \(z_2=r_2\cdot \; cis \; \theta_2\) with \(r_2\neq 0\), then \(z_1\cdot z_2=r_1\cdot r_2\cdot \; cis \; (\theta 1+\theta 2)\).
If \(z_1=z_2=z=r \; cis \; \theta \) then you can determine \(z_2\) and \(z_3\):
\(\begin{aligned} z^2 &=r\cdot r\cdot \; cis \; (\theta +\theta ) =r^2 \; cis \; (2\cdot \theta )\\ z^3&=r^3 \; cis \; (3\cdot \theta ) \end{aligned}\)
De Moivre’s Theorem simply generalizes this pattern to the power of any positive integer.
\(z^n=r^n\cdot \; cis \; (n\cdot \theta )\)
In addition to raising a complex number to a power, you can also take square roots, cube roots and \(n^{th}\) roots of complex numbers. Suppose you have complex number \(z=r \; cis \; \theta \) and you want to take the \(n^{th}\) root of z. In other words, you want to find a number \(v=s\cdot \; cis \; \beta \) such that \(v^n=z\). Do some substitution and manipulation:
\(\begin{aligned} v^n&=z \\ (s\cdot \; cis \; \beta )^n&=r\cdot \; cis \; \theta \\ s^n \cdot \; cis \; (n\cdot \beta )&=r\cdot \; cis \; \theta \end{aligned}\)
You can see at this point that to find s you need to take the \(n^{th}\) root of r. The trickier part is to find the angles, because \(n\cdot \beta \) could be any angle coterminal with \(\theta \). This means that there are \(n\) different \(n^{th}\) roots of \(z\).
\(\begin{aligned} n\cdot \beta &=\theta +2\pi k\\ \beta &=\dfrac{\theta +2\pi k}{n} \end{aligned}\)
The number \(k\) can be all of the counting numbers including zeros up to \(n−1\). So if you are taking the 4th root, then \(k=0,1,2,3\).
Thus the \(n^{th}\) root of a complex number requires n different calculations, one for each root:
\(v=\sqrt{n}{r} \cdot \; cis \; \left(\dfrac{\theta +2\pi k}{n}\right)\) for \({k \in I | 0\leq k\leq n−1}\)
To apply this formula, find the cube root of the number 8. Most students know that 23=8 and so know that 2 is the cube root of 8. However, they don’t realize that there are two other cube roots that they are mis\sin g. Remember to write out \(k=0,1,2\) and use the unit circle whenever possible to help you to find all three cube roots.
\(\begin{aligned}
8 &=8 \operatorname{cis} 0=(s \cdot \operatorname{cis} \beta)^{3} \\
z_{1} &=2 \cdot \operatorname{cis}\left(\frac{0+2 \pi \cdot 0}{3}\right)=2 \operatorname{cis} 0=2(\cos 0+i \cdot \sin 0)=2(1+0)=2 \\
z_{2} &=2 \cdot \operatorname{cis}\left(\frac{0+2 \pi \cdot 1}{3}\right)=2 \operatorname{cis}\left(\frac{2 \pi}{3}\right) \\
&=2\left(\cos \left(\frac{2 \pi}{3}\right)+i \cdot \sin \left(\frac{2 \pi}{3}\right)\right)=2\left(-\frac{1}{2}+\frac{\sqrt{3}}{2} i\right)=-1+i \sqrt{3} \\
z_{3} &=2 \cdot \operatorname{cis}\left(\frac{0+2 \pi \cdot 2}{3}\right)=2 \operatorname{cis}\left(\frac{4 \pi}{3}\right) \\
&=2\left(\cos \left(\frac{4 \pi}{3}\right)+i \cdot \sin \left(\frac{4 \pi}{3}\right)\right)=2\left(-\frac{1}{2}-\frac{\sqrt{3}}{2} i\right)=-1-i \sqrt{3}
\end{aligned}\)
The cube roots of 8 are 2, \(−1+i\sqrt{3} \), \(−1−i\sqrt{3} \).
To check, that they are the cube roots, cube them all simplify.
\(\begin{aligned} z^3_1 &=2^3=8\\ z^3_2&=(−1+i\sqrt{3} )^3 \\ &=(−1+i\sqrt{3} )\cdot (−1+i\sqrt{3} )\cdot (−1+i\sqrt{3} )\\ &=(1−2i\sqrt{3} −3)\cdot (−1+i\sqrt{3} ) \\ &=(−2−2i\sqrt{3} )\cdot (−1+i\sqrt{3} ) \\ &=2−2i\sqrt{3} +2i\sqrt{3} +6 \\&=8\end{aligned}\)
Note how many steps and opportunities there are for making a mistake when multiplying multiple terms in rectangular form. When you check z3, use trigonometric polar form.
\(\begin{aligned} z^3_3&=2^3 \; cis \; \left(3\cdot \dfrac{4\pi }{3}\right) \\ &=8(\cos 4\pi +i\cdot \sin 4\pi ) \\ &=8(1+0)\\&=8 \end{aligned}\)
Earlier, you were asked what a geometric interpretation of squaring a complex number is. Squaring a complex number produces a new complex number. The angle gets doubled and the magnitude gets squared, so geometrically you see a rotation.
Solution
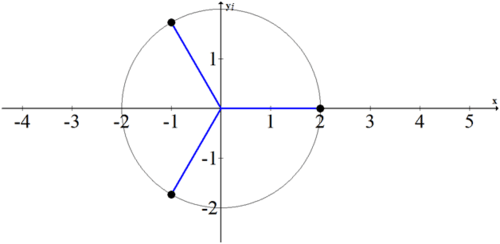
Plot the roots of 8 graphically and discuss any patterns you notice.
Solution
The three points are equally spaced around a circle of radius 2. Only one of the points, \(2+0i\), is made up of only real numbers. The other two points have both a real and an imaginary component which is why they are off of the x axis.
As you become more comfortable with roots, you can just determine the number of points that need to be evenly spaced around a certain radius circle and find the first point. The rest is just logic.
What are the fourth roots of \(16 \; cis \; 48^{\circ} \)?
Solution
There will be 4 points, each \(90^{\circ} \) apart with the first point at \(2 \; cis \; (12^{\circ} )\).
\(2 \; cis \; (12^{\circ} )\), \( 2 \; cis \; (102^{\circ} )\), \(2 \; cis \; (192^{\circ} )\), \(2 \; cis \; (282^{\circ} )\)
Solve for z by finding the \(n^{th}\) root of the complex number.
\(z^3=64−64\sqrt{3}i\)
Solution
First write the complex number in \(\; cis \;\) form. Remember to identify \(k=0,1,2\). This means the roots will appear every \(\sqrt{360^{\circ} }{3}=120^{\circ} \).
\(\begin{aligned} z^3 &=64−64\sqrt{3}i =128\cdot \; cis \; 300^{\circ} \\ z_1&=128^{\dfrac{1}{3}} \cdot \; cis \; \left(\dfrac{300}{3}\right)^{\circ} =128^{\dfrac{1}{3}} \cdot \; cis \; \left(\dfrac{300}{3}\right)^{\circ} \\ z_2 &=128^{\dfrac{1}{3}} \cdot \; cis \; (220^{\circ} )\\ z_3 &=128^{\dfrac{1}{3}} \cdot \; cis \; (340^{\circ} ) \end{aligned}\)
Use De Moivre’s Theorem to evaluate the following power.
\((\sqrt{2} −\sqrt{2} i)^6\)
Solution
First write the number in trigonometric polar form, then apply De Moivre’s Theorem and simplify.
\(\begin{aligned} (\sqrt{2} −\sqrt{2} i)^6&=(2 \; cis \; 315^{\circ} )^6 \\ &=2^6\cdot \; cis \; (6\cdot 315^{\circ} ) \\ &=64\cdot \; cis \; (1890^{\circ} ) \\ &=64\cdot \; cis \; (1890^{\circ} )\\&=64\cdot \; cis \; (90^{\circ} ) \\&=64(\cos 90^{\circ} +i\cdot \sin 90^{\circ} ) \\&=64(0+i) \\&=64i \end{aligned}\)
Review
Use De Moivre’s Theorem to evaluate each expression. Write your answers in rectangular form.
1. \((1+i)^5\)
2. \((1−\sqrt{3}i)^3\)
3. \((1+2i)^6\)
4. \((\sqrt{3}−i)^5\)
5. \(\left(\dfrac{1}{2}+\dfrac{i\sqrt{3}}{2}\right)^4\)
6. Find the cube roots of \(3+4i\).
7. Find the \(5^{th}\) roots of \(32i\).
8. Find the \(5^{th}\) roots of \(1+\sqrt{5}i\).
9. Find the \(6^{th}\) roots of - 64 and plot them on the complex plane.
10. Use your answers to #9 to help you solve \(x^6+64=0\).
For each equation: a) state the number of roots, b) calculate the roots, and c) represent the roots graphically.
11. \(x^3=1\)
12. \(x^8=1\)
13. \(x^{12}=1\)
14. \(x^4=16\)
15. \(x^3=27\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 11.4.
Vocabulary
| Term | Definition |
|---|---|
| \(n^{th}\) roots of unity | The \(n^{th}\) roots of unity are the \(n^{th}\) roots of the number 1. |
| complex number | A complex number is the sum of a real number and an imaginary number, written in the form \(a+bi\). |
| complex plane | The complex plane is the graphical representation of the set of all complex numbers. |
| De Moivre's Theorem | De Moivre's theorem is the only practical manual method for identifying the powers or roots of complex numbers. The theorem states that if \(z=r(\\cos \theta +i\\sin \theta )\) is a complex number in \(r\; cis \;\theta \) form and n is a positive integer, then \(z^n=r^n(\cos (n\theta )+i\sin (n\theta ))\). |
| trigonometric polar form | To write a complex number in trigonometric form means to write it in the form \(r\cos \theta +ri\sin \theta \). \(r\; cis \;\theta \) is shorthand for this expression. |
Additional Resources
Video: Determining the \(n^{th}\) Roots of a Complex Number
Practice: DeMoivre's Theorem and \(n^{th}\) Roots

