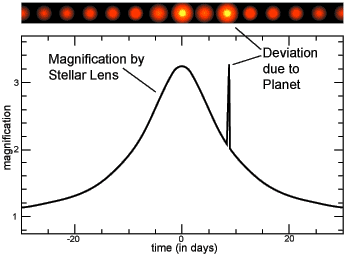
7.6: Microlensing
- Page ID
- 5639
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
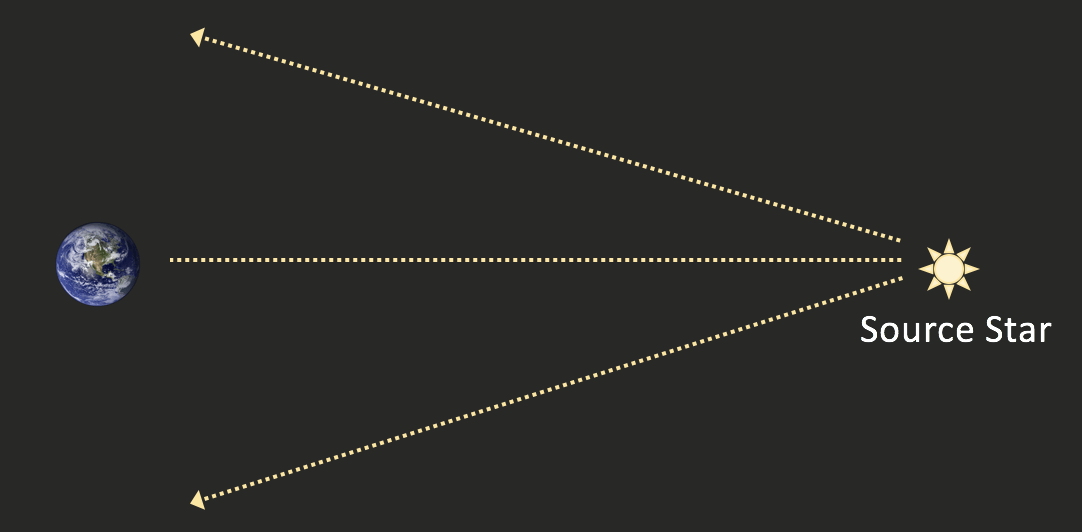
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Stars emit light in all directions. When we observe a distant star we only see the few rays of light from the star that are directed straight toward us. However, if a foreground star passes very close to our line of site of the more distant source star, the light from the distant background star will be gravitationally focused. To understand this idea, remember that we are the observer. The distant star is the source. The intervening star is the lens and it bends light from the source toward us. The two Figures below show the light path from a distant source star without and then with an intervening "lens" star.

Every object with mass has a gravitational field. We can think of objects with spherical symmetry, like stars or planets, as point sources. The strength of the gravitational field for a star is spherically symmetric. When we consider gravitational lensing, the relevant geometry is a slice through the sphere - a disk perpendicular to our line of site.
Qualitatively, the gravitational field at small radii on this disk (i.e., closest to the lensing object) is strongest and light from the source is bent so strongly that it converges closer to the lensing object and does not reach the observer. Likewise, the gravitational field is weakest at large radii on the disk and light from the source star focuses at distances beyond the observer. However, there is a ring on the disk where the bending of light from the source is "just right." Those rays of light from the source are brought to a focus at the position of the observer. This effect is called gravitational lensing and it was predicted in 1936 by Einstein. The ring of light that is focused at the position of the observer is given the special name of an Einstein ring.
Quantitatively, the size of the Einstein ring depends on the mass of the lens, the distance between the observer and the lens, DL, and the distance from the observer to the source, DS. Gravitational lensing occurs even if the lens star is too faint for us to see. Since most of the stars in galaxy are low mass, low luminosity M dwarf stars, this is often the case!
Since microlensing is an effect of gravity, it might seem like the amplitude of brightening will depend on the mass of the lens. While the mass of the lensing star determines the radius of the Einstein ring and the duration of the lensing event, the amplitude of brightening is most sensitive to something called the impact parameter. When the lensing object precisely lines up with our view to the source star, the impact parameter is zero and the magnification in brightness is a maximum. If the lensing object is not as tightly aligned with our view of the source - perhaps it just clips our view of the source star, then impact parameter is larger and the brightening of the source star (the "magnification") is not as strong. This is depicted in the figure below. The Einstein ring is represented by the dashed circle. The red, yellow, green and blue lines show the path that the lensing object travels with different offsets from precise alignment with our view of the source. The closer the alignment of the Einstein ring of the lens to our view of the source, the stronger the magnification that we observe. Gravitational lensing from objects as massive as stars typically last for several days.

The physical radius of the Einstein ring at the distance of the lens is described by the following equation:
\[R_E\,=\,2.2AU\sqrt{\frac{M}{0.3M_{star}}\,\frac{D_S}{8kpc}\,\frac{x(1-x)}{0.25}}\]
where x = DL/DS.
Gravitational lensing generally refers to the bending of light from a background source by a foreground massive object. Gravitational microlensing is a special case where multiple lensing events occur from more than one foreground mass. If the lensing star happens to have orbiting planets that also cross our line of site to the source star, then a second microlensing event is superimposed during the brightening event. Because the mass of the orbiting planet is smaller than the mass of a star, the duration of the second microlensing event will be shorter, but since the alignment of the lensing planet is essentially the same as the alignment of the host star, the amplitude of the magnification will be the similar.