4.1.7: Rules Based on Graphs
- Page ID
- 4308
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Function Rules based on Graphs
In the last two Concepts, you learned how to graph a function from a table and from a function rule. Now, you will learn how to find coordinate points on a graph and to interpret the meaning. Recall that each point on the graph has an x-value and y-value. When given an x-value, you will be asked to find its y-value.
Finding Coordinate Points on a Graph
The students at a local high school took The Youth Risk Behavior Survey. The graph below shows the percentage of high school students who reported that they were current smokers. (A current smoker is anyone who has smoked one or more cigarettes in the past 30 days.) What percentage of high-school students were current smokers in the following years?
- 1991
- 2004

1. First, find the value 1991 on the x-axis. This appears to be the first red point on the left side of the graph. By looking at the y-axis, it looks like this point has a y-value of approximately 27. This means that in 1991, approximately 27% of high school students reported that they were current smokers.
2. Find the value 2004 on the x-axis, which appears to be between the two red points on the right. This has an approximate y-value of 22.5. This means that in 2004, approximately 22.5% of high school students reported that they were current smokers.
Write a Function Rule from a Graph
Sometimes you’ll need to find the equation or rule of a function by looking at the graph of the function. Points that are on the graph can give you values of dependent and independent variables that are related to each other by the function rule. However, you must make sure that the rule works for all the points on the curve. In this course you will learn to recognize different kinds of functions and discover the rules for all of them. For now we’ll look at some simple examples and find patterns that will help us figure out how the dependent and independent variables are related.
The graph to the right shows the distance that an ant covers over time. Find the function rule that shows how distance and time are related to each other.
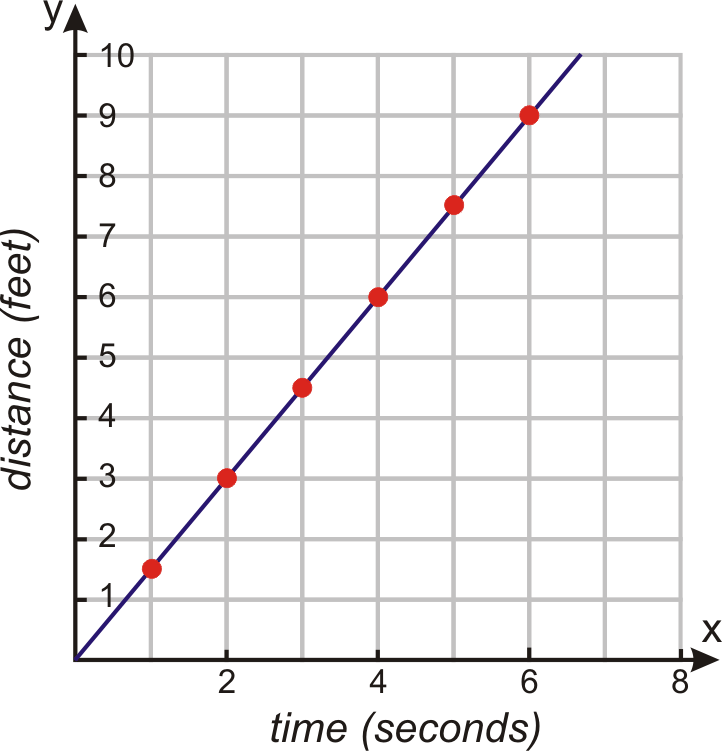
Let’s make a table of values of several coordinate points to see if we can spot how they are related to each other.
Time 0 1 2 3 4 5 6
Distance 0 1.5 3 4.5 6 7.5 9
We can see that for every second the distance increases by 1.5 feet. We can write the function rule as
Distance=1.5×time
The equation of the function is f(x)=1.5x.
Finding a Function Rule Described by a Graph
Find the function rule that describes the function shown in the graph.

Again, we can make a table of values of several coordinate points to identify how they are related to each other.
x −4 −3 −2 −1 0 1 2 3 4
y 8 4.5 2 .5 0 .5 2 4.5 8
Notice that the values of y are half of perfect squares: 8 is half of 16 (which is 4 squared), 4.5 is half of 9 (which is 3 squared), and so on. So the equation of the function is f(x)=(1/2)x2.
Example
Example \(\PageIndex{1}\)
Find the function rule that shows the volume of a balloon at different times, based on the following graph:

(Notice that the graph shows negative time. The negative time can represent what happened on days before you started measuring the volume.)
Solution
(Notice that the graph shows negative time. The negative time can represent what happened on days before you started measuring the volume.)
Once again, we make a table to spot the pattern:
Time −1 0 1 2 3 4 5
Volume 10 5 2.5 1.2 0.6 0.3 0.15
We can see that every day, the volume of the balloon is half what it was the previous day. On day 0, the volume is 5; on day 1, the volume is 5×(1/2); on day 2, it is 5×(1/2)×(1/2), and in general, on day x it is 5×(1/2)x. The equation of the function is f(x)=5×(1/2)x.
Review
For 1-4, the graph below shows the average life-span of people based on the year in which they were born. This information comes from the National Vital Statistics Report from the Center for Disease Control.
- What is the average life-span of a person born in 1940?
- What is the average life-span of a person born in 1955?
- What is the average life-span of a person born in 1980?
- What is the average life-span of a person born in 1995?

For 5-8, the graph below shows the median income of an individual based on his/her number of years of education. The top curve shows the median income for males and the bottom curve shows the median income for females. (Source: US Census, 2003.)
- What is the median income of a male that has 10 years of education?
- What is the median income of a male that has 17 years of education
- What is the median income of a female that has 10 years of education?
- What is the median income of a female that has 17 years of education?

For 9-11, write the function rule for each graph.
Review (Answers)
To view the Review answers, open this PDF file and look for section 1.14.
Vocabulary
| Term | Definition |
|---|---|
| coordinate point | A coordinate point is the description of a location on the coordinate plane. Coordinate points are written in the form (x, y) where x is the horizontal distance from the origin, and y is the vertical distance from the origin. |
| Function | A function is a relation where there is only one output for every input. In other words, for every value of x, there is only one value for y. |
| Function Rule | A function rule describes how to convert an input value (x) into an output value (y) for a given function. An example of a function rule is f(x)=x2+3. |
Additional Resources
PLIX: Play, Learn, Interact, eXplore: Function Rules Based on Graphs: Making Money in the Hat Business
Video: Solving Problems Involving the Distance and Midpoint Formulas
Practice: Rules Based on Graphs




