4.7.2: Write an Equation Given the Slope and a Point
- Page ID
- 4330
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Write an Equation Given the Slope and a Point
Suppose that you sent out a text message to all of your friends, asking them what information was needed to write the equation of a line. One of your friends responded that all you need is the slope of the line and a point on the line. Do you think that your friend was correct? If so, does it matter what point you have, and how could you use this information to come up with the equation?
Equations Given the Slope and a Point
Writing an Equation Given the y−Intercept
Previously, you learned how to graph solutions to two-variable equations in slope-intercept form. This Concept focuses on how to write an equation for a graphed line when given the slope and a point. There are two things you will need from the graph to write the equation in slope-intercept form:
- The y−intercept of the graph
- The slope of the line
Having these two pieces of information will allow you to make the appropriate substitutions in the slope-intercept formula. Recall the following:
Slope-intercept form: y=(slope)x+(y−intercept) or y=mx+b
Let's write an equation in slope-intercept form for each of the following situations:
- A line with a slope of 4 and a y−intercept of (0, –3).
Slope-intercept form requires two things: the slope and y−intercept. To write the equation, you substitute the values into the formula.
y=(slope)x+(y−intercept)
y=4x+(−3)
y=4x−3
You can also use a graphed line to determine the slope and y−intercept.
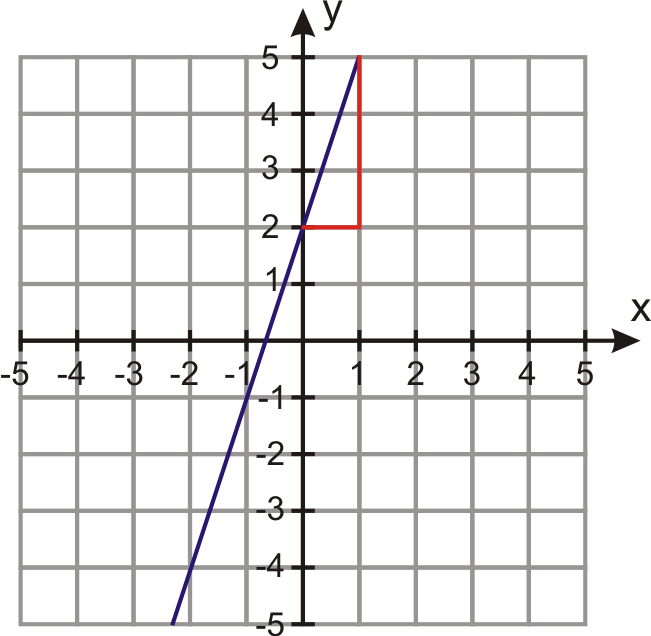
- The line shown in:
Figure 4.7.2.1
The y−intercept is (0, 2). Using the slope triangle, you can determine the slope is riserun=−3/−1=3/1. Substituting the value 2 for b and the value 3 for m, the equation for this line is y=3x+2.
Writing an Equation Given an Ordered Pair
You will not always be given the y−intercept, but sometimes you will be given any point on the line. When asked to write the equation given a graph, it may be difficult to determine the y−intercept. Perhaps the y−intercept is rational instead of an integer. Maybe all you have is the slope and an ordered pair. You can use this information to write the equation in slope-intercept form. To do so, you will need to follow several steps:
Step 1: Begin by writing the formula for slope-intercept form: y=mx+b.
Step 2: Substitute the given slope for m.
Step 3: Use the ordered pair you are given (x,y) and substitute these values for the variables x and y in the equation.
Step 4: Solve for b (the y−intercept of the graph).
Step 5: Rewrite the original equation in Step 1, substituting the slope for m and the y−intercept for b.
Let's write an equation in slope-intercept form for the following line:
A line with a slope of 4 that contains the ordered pair (–1, 5).
Step 1: Begin by writing the formula for slope-intercept form.
y=mx+b
Step 2: Substitute the given slope for m.
y=4x+b
Step 3: Use the ordered pair you are given, (–1, 5), and substitute these values for the variables x and y in the equation.
5=(4)(−1)+b
Step 4: Solve for b (the y−intercept of the graph).
5=−4+b
5+4=−4+4+b
9=b
Step 5: Rewrite y=mx+b, substituting the slope for m and the y−intercept for b.
y=4x+9
Examples
Example 4.7.2.1
Earlier, you were asked if you only need the slope of a line and a point on the line to write the equation of a line.
Solution
You can write the equation of a line with just the slope and a point on the line. As shown in this concept, if you have the slope and the y−intercept, you can easily write the equation in slope-intercept form y=mx+b. If you do not have the y−intercept and instead just have a random point on the line, you can plug the ordered pair and the slope into the general equation and solve for b (the y−intercept of the graph).
Example 4.7.2.2
Write the equation for a line with a slope of –3 containing the point (3, –5).
Solution
Using the five-steps from above:
y=(slope)x+(y−intercept)
y=−3x+b
−5=−3(3)+b
−5=−9+b
4=b
y=−3x+4
Review
- What is the formula for slope-intercept form? What do the variables m and b represent?
- What are the five steps needed to determine the equation of a line given the slope and a point on the graph (not the y−intercept)?
In 3–13, find the equation of the line in slope–intercept form.
- The line has a slope of 7 and a y−intercept of –2.
- The line has a slope of –5 and a y−intercept of 6.
- The line has a slope of -2 and a y−intercept of 7.
- The line has a slope of 2/3 and a y−intercept of 4/5.
- The line has a slope of −1/4 and contains the point (4, –1).
- The line has a slope of 2/3 and contains the point (12,1).
- The line has a slope of –1 and contains the point (45,0).
- The slope of the line is −2/3, and the line contains the point (2, –2).
- The slope of the line is –3, and the line contains the point (3, –5).
-
Figure 4.7.2.2 -
Figure 4.7.2.3
Review (Answers)
To see the Review answers, open this PDF file and look for section 5.1.
Vocabulary
| Term | Definition |
|---|---|
| undefined slope | An undefined slope cannot be computed. Vertical lines have undefined slopes. |
| zero slope | A line with zero slope is a line without any steepness, or a horizontal line. |
| Intercept | The intercepts of a curve are the locations where the curve intersects the x and y axes. An x intercept is a point at which the curve intersects the x-axis. A y intercept is a point at which the curve intersects the y-axis. |
Additional Resources
Video: Writing Linear Equations in Point-Slope Form Given Information
Activity: Write an Equation Given the Slope and a Point Discussion Questions
Study Aid: Determining the Equation of a Line Study Guide
Practice: Write an Equation Given the Slope and a Point
Real World Application: Bangladesh