1.1.1: Relations and Functions
- Page ID
- 14118
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Finding the Domain and Range of Functions
You just got a new part-time job at the mall that pays a base rate of $150/week plus $5/sale. Your boss encourages you to make as many sales as possible but she will cap your weekly earnings at $250. What are the domain and range of the function represented by this situation?
Domain and Range of a Function
The input and output of a function is also called the domain and range. The domain of a function is the set of all input values. The range of a function is the set of all output values. Sometimes, a function is a set of points. In this case, the domain is all the x− values and the range is all the y− values. Functions can also be linear and polynomial equations. In these instances, you need to graph the function to see where it is defined. You may notice that some functions are defined for “all real numbers.” The symbol, ℝ, is used to denote the set of all real numbers.
Let's determine if {(9, 2), (7, -3), (4, -6), (-10, 4), (-2, -7)} is a function. If so, we will find the domain and range.
First, this is a function because the x− values do not repeat. To find the domain, we need to list all the x− values. The range is all the y− values. Typically, you would list the values in the order they appear. Notice the notation.
x∈{9,7,4,−10,−2}
y∈{2,−3,−6,4,−7}
The ∈ symbol means “an element of/in.” The braces, { }, around the x and y−values, indicate that each is a set. In words, you would say, “x is an element in the set 9, 7, 4, -10, and 2.” Depending on the text, you may see “:” (colon) interchanged with the “∈” symbol and sets without { } around them.
Let's find the domain and range for the following problems.
- y=x−3
Because this is a linear equation we also know that it is a linear function. All lines continue forever in both directions, as indicated by the arrows.
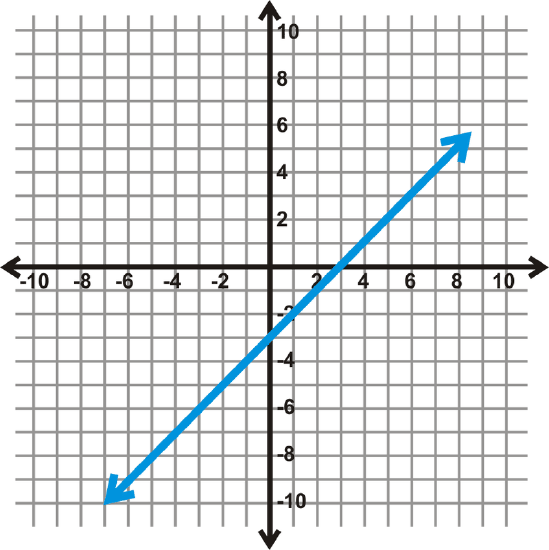
[Figure1]
Notice the line is solid, there are no dashes or breaks. This means that it is continuous. A continuous function has a value for every x, or the domain is all real numbers. Can you plug in ANY value for x and get a y−value? Yes. There are a few ways to write this.
Domain: x∈ℝ, x∈(−∞,∞), x is all reals
In words, x is an element in the set of real numbers.
The second option, (−∞,∞), is an interval, not a point. The parenthesis indicate that infinity, ∞, and negative infinity, −∞, are not included in the interval, but every number between them is. To include an endpoint in the interval, use [ or ] brackets. This is called interval notation.
The range of this function is also continuous. Therefore, the range is also the set of all real numbers. We can write the range in the same ways we wrote the domain, but with y instead of x.
Range: y∈ℝ or y∈(−∞,∞)
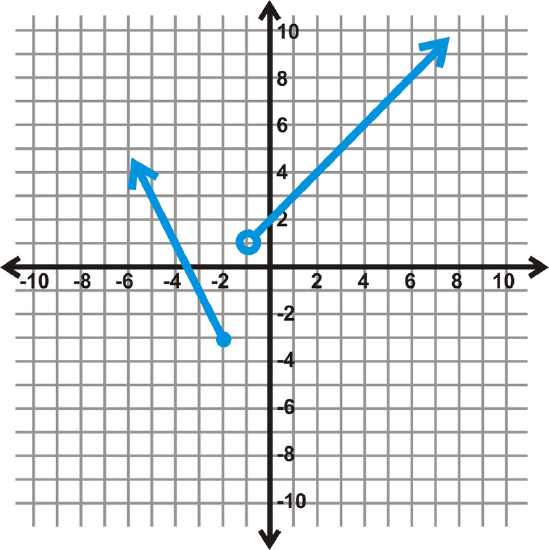
This is a function, even though it might not look like it. This type of function is called a piecewise function because it pieces together two or more parts of other functions.
To find the domain, look at the possible x−values. Notice that when x is between -2 and -1 it is not defined, or there are no x−values.
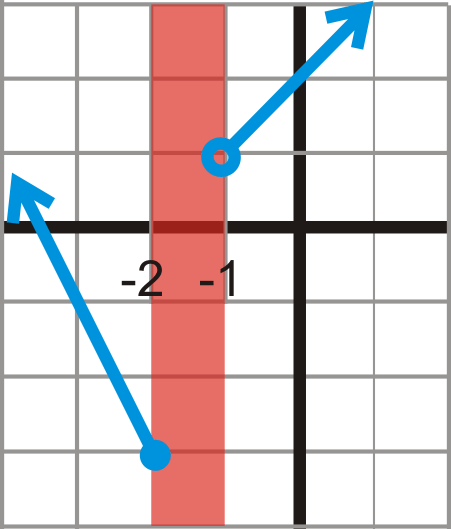
[Figure3]
Mathematically, this would be written: x∈(−∞,−2]∪(−1,∞). The ∪ symbol means “union.” In words, the domain is “all real numbers except those between -2 and -1.” Notice that -2 is included in the domain because the dot at -2 is closed. To find the range, we need to look at the possible y−values. Changing our viewpoint to look at the y−axis, at first glance, it looks like the function is not defined from 1 to -3.
However, upon further investigation, the branch on the left does pass through the yellow region, where we though the function was not defined. This means that the function is defined between 1 and -3 and thus for all real numbers. However, below -3, there are no y−values. The range is y∈[−3,∞).
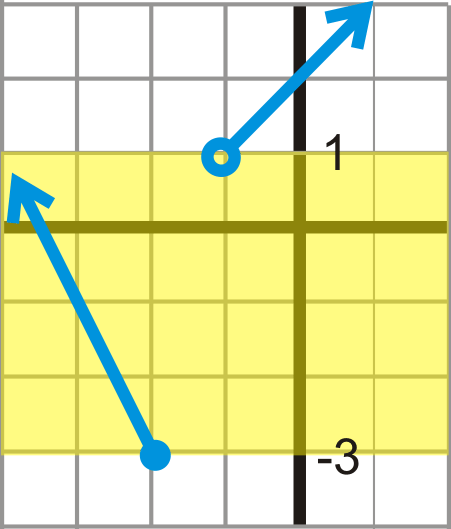
[Figure4]
Examples
Earlier, you were asked to find the domain and range of the function of your sales, where you make a base rate of $150/week plus $5/sale (your weekly earnings are capped at $250/week).
Solution
The function represented by this situation can be written as y=150+5x, where x is the number of sales you make. You can't make a negative number of sales, so the least amount of sales you can make is zero. To find the maximum number of sales before you reach the cap, we must plug in $250 for y.
250=150+5x
100=5x
x=20
Therefore, the domain of the function is 0≤x≤20.
To find the range, plug the two extremes of the domain into the equation. When x equals 0, y equals 150, and when x equals 20, y equals 250.
Therefore the range of the function is 150≤y≤250.
Find the domain and range of the following function: {(8, 3), (-4, 2), (-6, 1), (5, 7)}.
Solution
Domain: x∈{8,−4,−6,5} Range: y∈{3,2,1,7}
Find the domain and range of the following function: y=−\(\ 1\over 2\)x+4.
Solution
Domain: x∈ℝ Range: y∈ℝ
Find the domain and range of the following function.
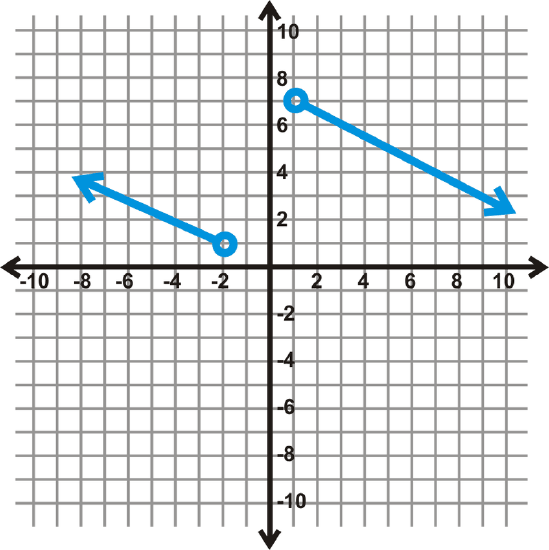
[Figure5]
Solution
This is a piecewise function. The x−values are not defined from -2 to 1. The range looks like it is not defined from 1 to 7, but the lines continue on, filling in that space as x gets larger, both negatively and positively.
Domain: x∈(−∞,−2)∪(1,∞) Range: y∈ℝ
Find the domain and range of the following function.
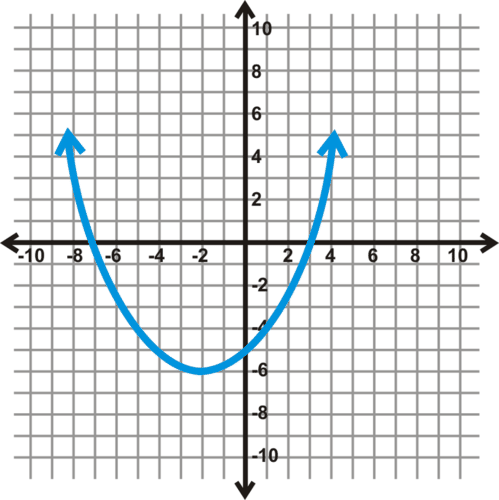
[Figure6]
Solution
This is a parabola, the graph of a quadratic equation. Even though it might not look like it, the ends of the graph continue up, infinitely, and x keeps growing. In other words, x is not limited to be between -9 and 5. It is all real numbers. The range, however, seems to start at -6 and is all real numbers above that value.
Domain: x∈ℝ Range: y∈[−6,∞)
Review
Determine if the following sets of points are functions. If so, state the domain and range.
- {(5, 6), (-1, 5), (7, -3), (0, 9)}
- {(9, 8), (-7, 8), (-7, 9), (8, 8)}
- {(6, 2), (-5, 6), (-5, 2)}
- {(-1, 2), (-6, 3), (10, 7), (8, 11)}
- {(5, 7), (3, 7), (5, 8), (8, 1)}
- {(-3, -4), (-5, -6), (1, 2), (2, -6)}
Find the domain and range of the following functions.
- y=3x−7
- 6x−2y=10
9.
[Figure7]
10.
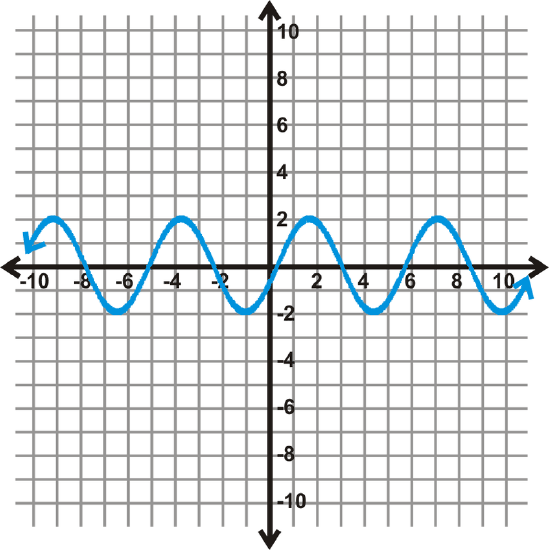
[Figure8]
11.
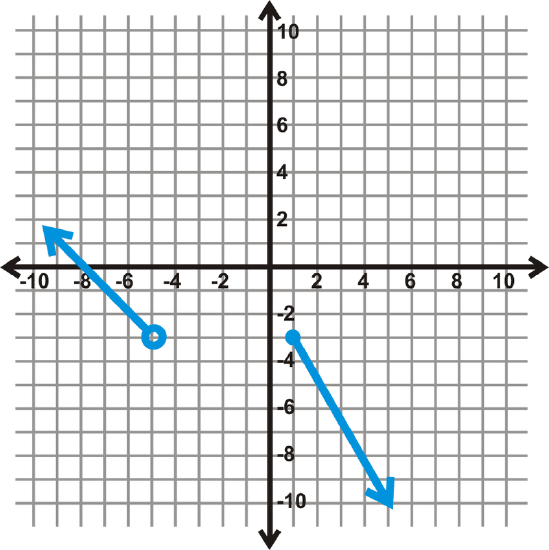
[Figure9]
12.
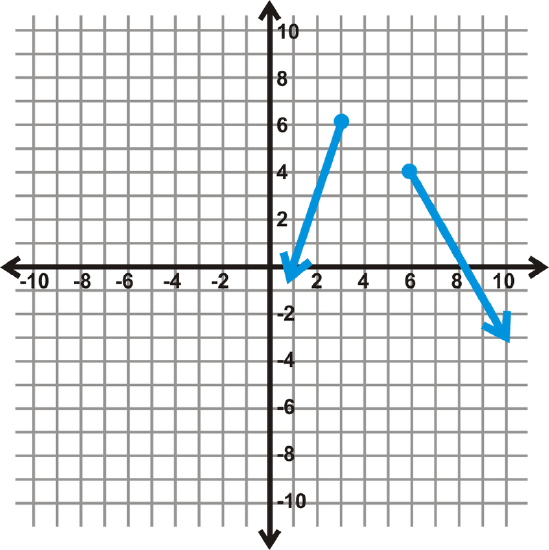 [Figure10]
[Figure10]13.
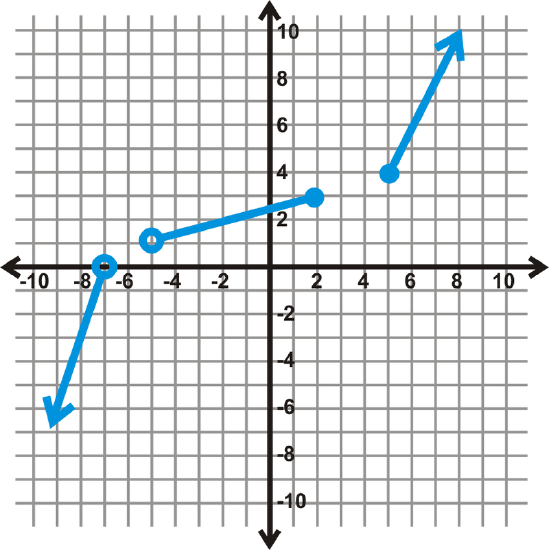
14. Challenge
15. Writing Make a general statement about the domain and range of all linear functions. Use the proper notation.
Vocabulary
| Term | Definition |
|---|---|
| closed interval | A closed interval includes the minimum and maximum values (endpoints) of the interval. |
| Continuous Function | A continuous function is a function without breaks or gaps. It contains an infinite, uncountable number of values. |
| Function | A function is a relation where there is only one output for every input. In other words, for every value of x, there is only one value for y. |
| open interval | An open interval does not include the endpoints of the interval. |
| Piecewise Function | A piecewise function is a function that pieces together two or more parts of other functions to create a new function. |
| Relation | A relation is any set of ordered pairs (x,y). A relation can have more than one output for a given input. |
| union | ∪ is a symbol that stands for union and is used to connect two groups together. It is associated with the logical term OR. |
Image Attributions
[Figure 1]
Credit: Laura Guerin;CK-12 Foundation
Source: CK-12 Foundation
[Figure 2]
Credit: Laura Guerin;CK-12 Foundation;CK-12 Foundation, Larame Spence
Source: CK-12 Foundation;Desmos Graphing Calculator
[Figure 3]
Credit: Laura Guerin;CK-12 Foundation
Source: CK-12 Foundation
[Figure 4]
Credit: Laura Guerin;CK-12 Foundation
Source: CK-12 Foundation
[Figure 5]
Credit: Laura Guerin;CK-12 Foundation
Source: CK-12 Foundation
[Figure 6]
Credit: Laura Guerin;CK-12 Foundation
Source: CK-12 Foundation
[Figure 7]
Credit: Laura Guerin;CK-12 Foundation
Source: CK-12 Foundation
[Figure 8]
Credit: Laura Guerin;CK-12 Foundation
Source: CK-12 Foundation
[Figure 9]
Credit: Laura Guerin;CK-12 Foundation
Source: CK-12 Foundation
[Figure 10]
Credit: CK-12 Foundation, Larame Spence
Source: Desmos Graphing Calculator

