2.1.2: Graphs of Quadratic Functions
- Page ID
- 14190
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Graphs of Quadratic Functions
In prior lessons, we have discussed the standard form of a quadratic function: f(x)=ax2+bx+c. You may have seen other forms, such as the vertex form, or the factored form. Why are there so many common ways to write the same equations? Why should we learn all these different forms if the standard form is the most common anyway?
Graphing Quadratic Functions
Quadratic Functions
A function f defined by f(x)=ax2+bx+c, where a,b, and c are real numbers and a≠0, is called a quadratic function.
The defining characteristic of a quadratic function is that it is a polynomial whose highest exponent is 2.
There are several ways to write quadratic functions:
- standard form, the form of the quadratic function above: f(x)=ax2+bx+c
- vertex form, commonly used for quick sketching: f(x)=a(x−h)2+k
- factored form, excellent for finding x-intercepts: f(x)=a(x−r1)(x−r2)
The y−intercept of a quadratic function in standard form is (0,c) and it is found by substituting for x in f(x)=ax2+bx+c.
Summary of Vertex Form
Given a quadratic function in vertex form: f(x)=a(x−h)2+k:
- The vertex is at (h,k)
- The parabola opens up if a>0
- The parabola opens down if a<0
- The parabola is narrower than y=x2 if |a|>1
- The parabola opens wider than y=x2 if |a|<1
Vertex of a Parabola
In the standard form of a quadratic function, the x−coordinate of the vertex of the parabola is given by the equation:
\(\ x=-\frac{b}{2 a}\)
The y−coordinate of the vertex is found with:
\(\ y=f\left(-\frac{b}{2 a}\right)\)
Axis of Symmetry of a Parabola
A parabola has reflective symmetry about a vertical line through the vertex.
The vertical line \(\ x=-\frac{b}{2 a}\) is also the parabola's axis of symmetry.
Examples
Graph g(x)=x2+6x+7 using transformations.
Solution
First, complete the square to write this function in vertex form. Add and subtract \(\ \left(\frac{b}{2}\right)^{2}\) to the right hand side of the equation:
g(x)=x2+6x+7
=x2+6x+9+7−9
Now, factor the right hand side:
g(x)=(x+3)2−2
Thus, a=1 and the vertex of this parabola is (-3, -2). We know that the parabola opens up with the same width as y=x2 and it has a minimum value at the vertex. The graph of the parabola is below.

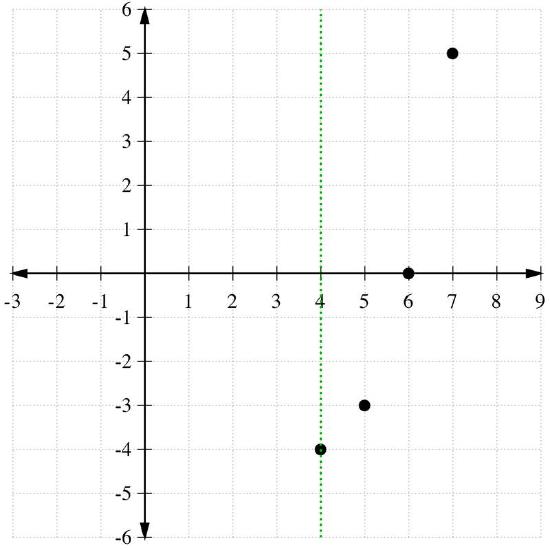
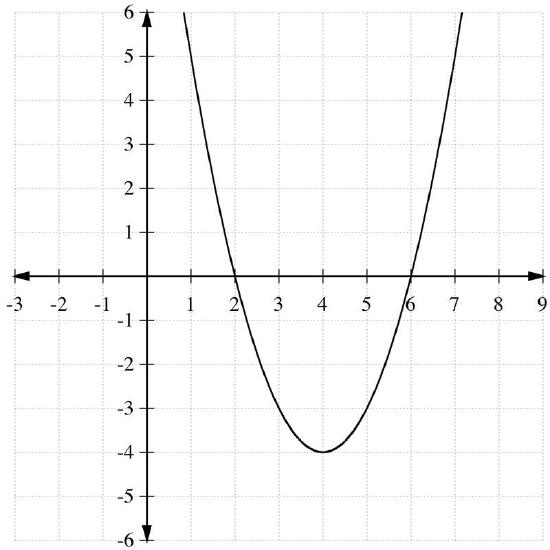
Find the vertex and graph the quadratic function g(x)=x2−8x+12.
Solution
The x−coordinate of the vertex is \(\ x=-\frac{-8}{2}=4\).
The y−coordinate of the vertex is g(4)=(4)2−8(4)+12=16−32+12=−4
Thus the vertex is at (4, -4).
To graph the parabola, we will make a table of points staring with the x−coordinate of 4:
| x | y=g(x) |
|---|---|
| 4 | -4 |
| 5 | -3 |
| 6 | 0 |
| 7 | 5 |
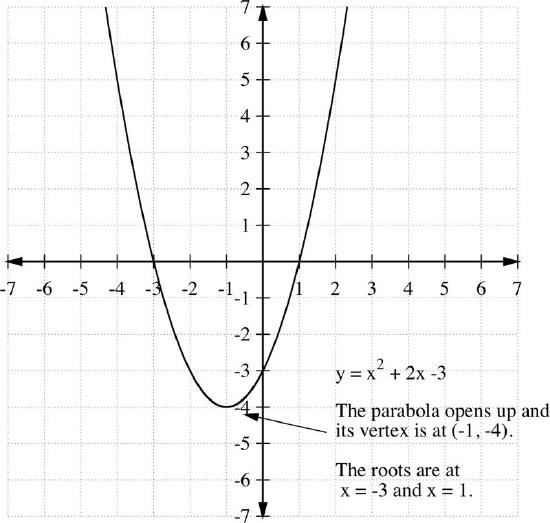
Sketch the graph of the function y=f(x)=x2+2x−3.
Solution
Let's first find the intercepts. For the y−intercept, if x=0, then f(0)=−3, or y=−3, so the y−intercept point is (0, -3).
Now, for the x−intercepts, if y=f(x)=0, then x2+2x−3=0, or x2+2x−3=(x+3)(x−1)=0
so that x=−3 and x=1 are the x−intercepts, that is (-3, 0) and (1, 0).
The vertex (extreme point) is at
\(\ x=\frac{-b}{2 a}=\frac{-2}{2(1)}=-1\)
Since
\(\ \begin{aligned}
f(-1) &=(-1)^{2}+2(-1)-3 \\
&=-4
\end{aligned}\)
The vertex is (-1, -4).
Since the coefficient of x2 is positive, a>0, the extreme point is a minimum and the parabola opens up. From this information, we can make a rough sketch of the parabola containing the points determined above. Notice that the range of the function is y≥−4.
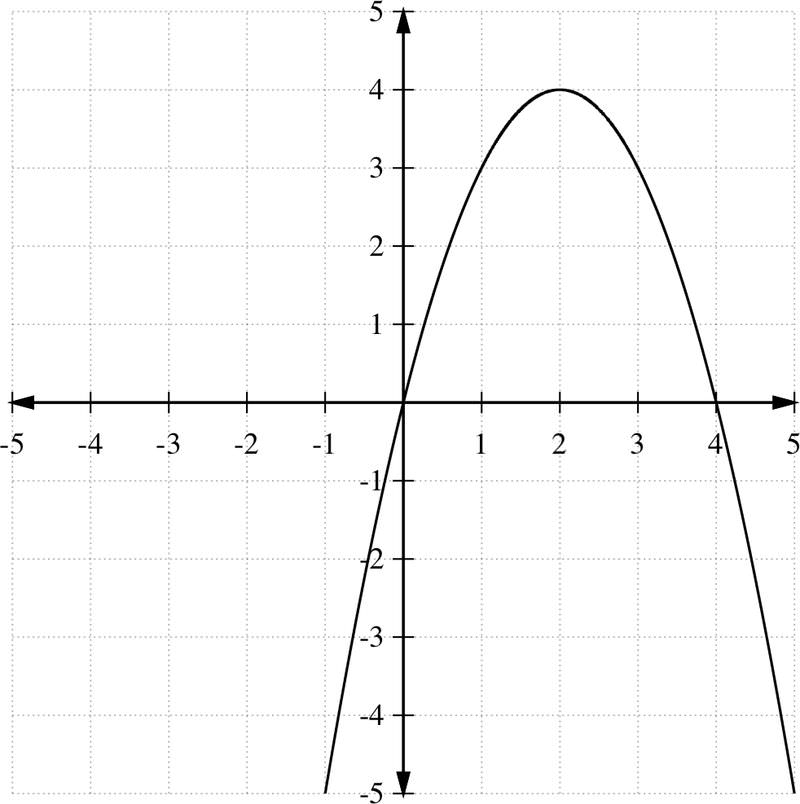
Sketch the graph of the quadratic function f(x)=−x2+4x.
Solution
To find the y−intercept, set x=0, and f(0)=−(0)2+4(0)=0
Thus the parabola intercepts the y−axis at the origin.
The x−intercept is obtained by setting y=0. Thus, −x2+4x=0.
Factoring,
−x2+4x=−x(x−4)=0
so that x=0 and x=4 are the x−intercepts.
We have a=−1 and b=4, so that the extreme point occurs when
\(\ x=\frac{-b}{2 a}=\frac{-4}{2(-1)}=2\)
Since f(2)=−(2)2+4(2)=−4+8=4, then (2, 4) is the extreme point. It is a maximum point since a=−1<0 and the parabola opens down. Finally, the graph can be obtained by sketching a parabola through the points determined above. From graph, the range of the function is y≤4.
Sketch the graph of y=−3(x−2)2+1.
Solution
The equation y=−3(x−2)2+1 is already in vertex form, so graphing is relatively easy:
Recall the when the equation is written in vertex form like this, the vertex is the point (h,k):
vertex form: y=a(x−h)2+k
Our equation: y=−3(x−2)2+1
Examining our equation, we can see the vertex of the parabola is at (2, 1).
To find another point on the parabola solve for an x value.
Since the vertex is at x = 2, let's try one unit to the right: x = 3.
−3(3−2)2+1=−2
∴ There is a point on the parabola at (3, -2)
Since a parabola has an axis of symmetry that passes through its vertex, we can reflect the point (3, -2) across the axis of symmetry to get another point, (1, -2) also on the parabola.
The graph of y=−3(x−2)2+1 is shown below, using vertex (2, 1) and points (3, -2) and (1, -2).
Review
- What is the U-Shaped graph of a quadratic function called?
- Which direction does a parabola open if the leading coefficient (a) is positive?
- For y2=x If the coefficient of y is positive, which way does the parabola open?
- What is the name of the lowest point of a parabola that opens up and the highest point of a parabola that opens down.
- What is the name of the line passing through the vertex that divides the parabola into two symmetric parts?
- Sketch the graph of y=x2+3
- Sketch the graph of y=−x2+4x−4
- Sketch the graph of y=2x2+8x
- Consider the following quadratic function: y=−x2−2x+1 a) Which direction does it open? b) What is the vertex? c) Is it stretched in any way?
- Consider the quadratic functions: y=2x2 y=4x2 y=6x2 Which quadratic function would you expect to have the narrowest parabola? Explain your answer.
Sketch the graph of each function:
- y=−x2
- y=3x2+6x+1
- y=12x2+2x+4
- y=(x−3)2+4
- y=−x2−8x−17
The quadratic function y=−0.05x2+1.5x can be used to represent the path of a football kicked 30 yards down the field. The variable x represents the distance, in yards, the ball has traveled down the field. The height, in yards, of the football in the air is represented by the variable (y).
Use the quadratic function to calculate the height of the ball as it travels down the field. Round your answers to the nearest hundredth of a yard.
| Distance Down the Field (yds) | Height in the Air (yds) |
|---|---|
| 0.0 | |
| 5.0 | |
| 10.0 | |
| 15.0 | |
| 20.0 | |
| 25.0 | |
| 30.0 |
- What is the maximum height of the football during the kick?
- How far down the field has the football traveled when it reaches its maximum height?
- Use the information in the table to graph the path of the football kick.
- If you were shown only the graph of this quadratic function, how could you determine the maximum height of the football during the kick and how far down the field the football has traveled when it reaches its maximum height?
Vocabulary
| Term | Definition |
|---|---|
| axis of symmetry | The axis of symmetry of a parabola is a vertical line that passes through the vertex of the parabola. The parabola is symmetrical about this line. |
| factored form | The factored form of a quadratic function f(x) is f(x)=a(x−r1)(x−r2), where r1 and r2 are the roots of the function. |
| Intercept | The intercepts of a curve are the locations where the curve intersects the x and y axes. An x intercept is a point at which the curve intersects the x-axis. A y intercept is a point at which the curve intersects the y-axis. |
| Maximum | The maximum is the highest point of a graph. The maximum will yield the largest value of the range. |
| Maximum/Minimum | The maximum is the highest point of a function and the minimum is the lowest point of a function. |
| Minimum | The minimum is the lowest point of a graph. The minimum will yield the smallest value of the range. |
| Parabola | A parabola is the characteristic shape of a quadratic function graph, resembling a "U". |
| quadratic function | A quadratic function is a function that can be written in the form f(x)=ax2+bx+c, where a, b, and c are real constants and a≠0. |
| standard form | The standard form of a quadratic function is f(x)=ax2+bx+c. |
| Transformations | Transformations are used to change the graph of a parent function into the graph of a more complex function. |
| Vertex | The vertex of a parabola is the highest or lowest point on the graph of a parabola. The vertex is the maximum point of a parabola that opens downward and the minimum point of a parabola that opens upward. |
| Vertex form | The vertex form of a quadratic function is y=a(x−h)2+k, where (h,k) is the vertex of the parabola. |

