2.3.3: Graphs of Rational Functions when the Degrees are not Equal

Last updated
Save as PDF

Page ID: 14198

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

Graphing when the Degrees of the Numerator and Denominator are Different

Xerxes says that the function \(\ y=\frac{x-2}{4 x^{2}+7}\), has a horizontal asymptote of \(\ y=\frac{1}{4}\), Yolanda says the function has no horizontal asymptote, Zeb says that it does have a horizontal asymptote but it's at y=0. Which one of them is correct?

Graphing Rational Functions

In this concept we will touch on the different possibilities for the remaining types of rational functions. You will need to use your graphing calculator throughout this concept to ensure your sketches are correct.

Let's graph \(\ y=\frac{x+3}{2 x^{2}+11 x-6}\) and find all asymptotes, intercepts, and the domain and range.

In this problem the degree of the numerator is less than the degree of the denominator. Whenever this happens the horizontal asymptote will be y=0, or the x-axis. Now, even though the x-axis is the horizontal asymptote, there will still be a zero at x=−3 (solving the numerator for x and setting it equal to zero). The vertical asymptotes will be the solutions to 2x²+11x−6=0. Factoring this quadratic, we have (2x−1)(x+6)=0 and the solutions are \(\ x=\frac{1}{2}\) and −6. The y-intercept is \(\ \left(0,-\frac{1}{2}\right)\). At this point, we can plug our function into the graphing calculator to get the general shape.

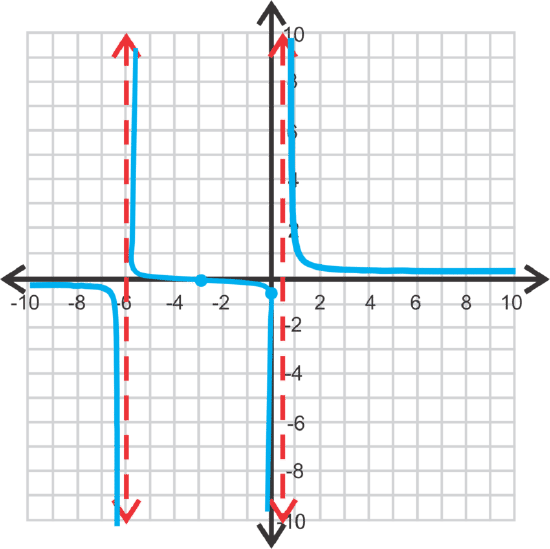
f-d_536edfef452f720366ac87fe8b6eb420cd50e2a8d2482713f3b26e62+IMAGE_TINY+IMAGE_TINY.png

Because the middle portion crosses over the horizontal asymptote, the range will be all real numbers. The domain is \(\ x \in \mathbb{R} ; x=-6 ; x \neq \frac{1}{2}\).

Be careful when graphing any rational function. This function does not look like the graph to the left in a TI-83/84. This is because the calculator does not have the ability to draw the asymptotes separately and wants to make the function continuous. Make sure to double-check the table (2^nd→ GRAPH) to find where the function is undefined.

Now, let's graph \(\ f(x)=\frac{x^{2}+7 x-30}{x+5}\) and find all asymptotes, intercepts, and the domain and range.

In this problem the degree of the numerator is greater than the degree of the denominator. When this happens, there is no horizontal asymptote. Instead there is a slant asymptote. Recall that this function represents division. If we were to divide x²+7x−30 by x+5, the answer would be \(\ x+2-\frac{20}{x+5}\). The slant asymptote would be the answer, minus the remainder. Therefore,for this problem the slant asymptote is y=x+2. Everything else is the same. The y-intercept is \(\ \frac{-30}{5} \rightarrow(0,-6)\) and the x-intercepts are the solutions to the numerator, x²+7x−30=0→(x+10)(x−3)→x=−10,3. There is a vertical asymptote at x=−5. At this point, you can either test a few points to see where the branches are or use your graphing calculator.

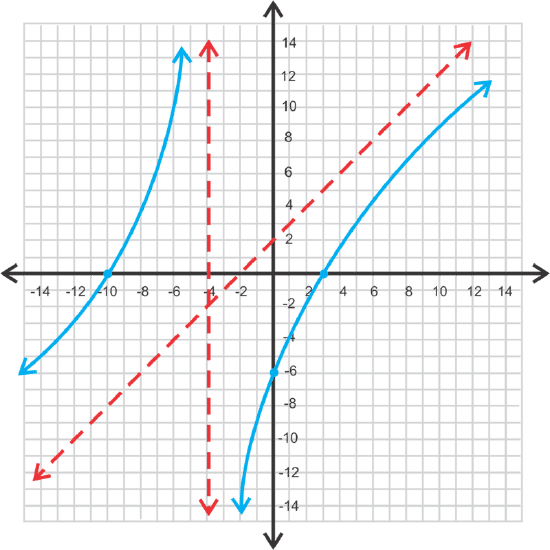f-d_7267868743fe75de7a292cbca95e2c654f54344c0f225e94fab86497+IMAGE_TINY+IMAGE_TINY.png

The domain would be all real numbers; x≠−5. Because of the slant asymptote, there are no restrictions on the range. It is all real numbers.

Finally, let's graph \(\ y=\frac{x-6}{3 x^{2}-16 x-12}\) and find the asymptotes and intercepts.

Because the degree of the numerator is less than the degree of the denominator, there will be a horizontal asymptote along the x-axis. Next, let’s find the vertical asymptotes by factoring the denominator; (x−6)(3x+2). Notice that the denominator has a factor of (x−6), which is the entirety of the numerator. That means there will be a hole at x=6.

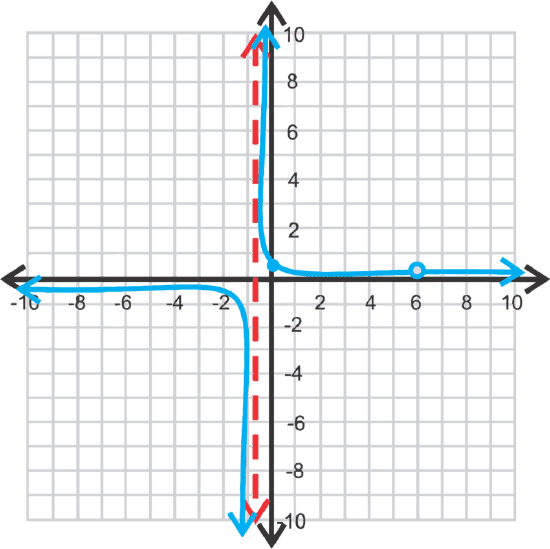
f-d_dc754448310e9a3ef3b0a6e1f9754d74e3a2cc212eb491c44365cf2c+IMAGE_TINY+IMAGE_TINY.png

Therefore, the graph of \(\ y=\frac{x-6}{3 x^{2}-16 x-12}\) will be the same as \(\ y=\frac{1}{3 x+2}\) except with a hole at x=6. There is no x-intercept, the vertical asymptote is at x=-\frac{2}{3} and the y-intercept is \(\ \left(0, \frac{1}{2}\right)\).

Recap

For a rational function; \(\ f(x)=\frac{p(x)}{q(x)}=\frac{a_{m} x^{m}+\ldots+a_{0}}{b_{n} x^{n}+\ldots+b_{0}}\)

If m<n, then there is a horizontal asymptote at y=0.
If m=n, then there is a horizontal asymptote at \(\ y=\frac{a_{m}}{b_{n}}\) (ratio of the leading coefficients).
If m>n, then there is a slant asymptote at \(\ y=\left(a_{m} x^{m}+\ldots+a_{0}\right) \div\left(b_{n} x^{n}+\ldots+b_{0}\right)\) without the remainder. In this concept, we will only have functions where m is one greater than n.

Examples

Example 1

Earlier, you were asked to determine which student is correct.

Solution

The degree of the numerator x−2 is less than the degree of the denominator 4x²+7. We know that whenever this happens the horizontal asymptote will be y=0, or the x-axis.

Therefore, Zeb is correct.

Graph the following functions. Find any intercepts and asymptotes.

Example 2

\(\ y=\frac{3 x+5}{2 x^{2}+9 x+20}\)

Solution

x-intercept: \(\ \left(-\frac{5}{3}, 0\right)\), y-intercept: \(\ \left(0, \frac{1}{4}\right)\)

horizontal asymptote: y=0

vertical asymptotes: none

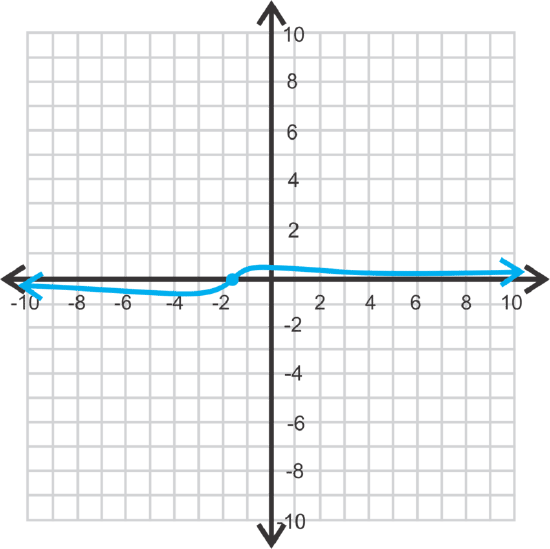f-d_c142cc9c51ce40ddb263e877033ec56061ca493a76508188c4c09010+IMAGE_TINY+IMAGE_TINY.png

Example 3

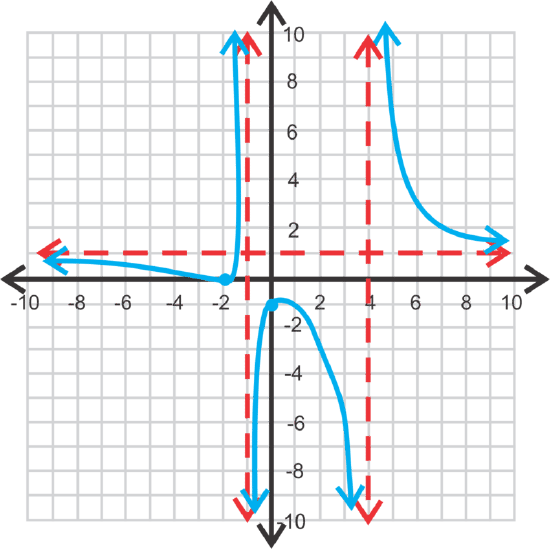
\(\ f(x)=\frac{x^{2}+4 x+4}{x^{2}-3 x-4}\)

Solution

x-intercept: (−2,0), y-intercept: (0,−1)

horizontal asymptote: y=1

vertical asymptotes: x=4 and x=−1

f-d_b016693e7c2394e771f9a715d89ec9746041bd75802b13394d87acf1+IMAGE_TINY+IMAGE_TINY.png

Example 4

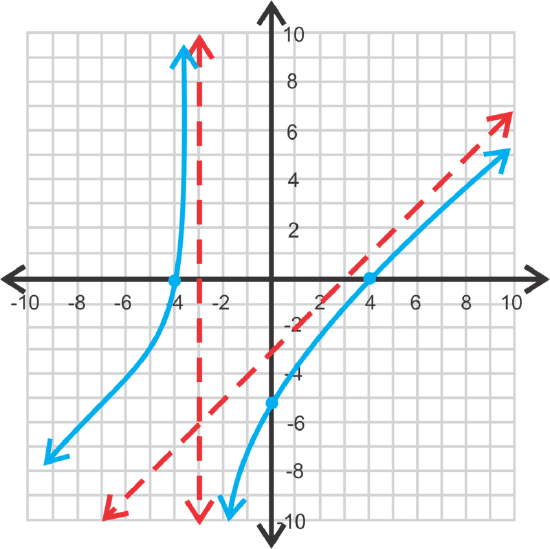
\(\ g(x)=\frac{x^{2}-16}{x+3}\)

Solution

x-intercepts: (−4,0) and (4,0)

y-intercept: \(\ \left(0,-\frac{16}{3}\right)\)

slant asymptote: y=x−3

vertical asymptotes: x=−3

f-d_4390278c3cb44070b613e81066f31af26490d5a3a7f13a334c0298fe+IMAGE_TINY+IMAGE_TINY.png

Example 5

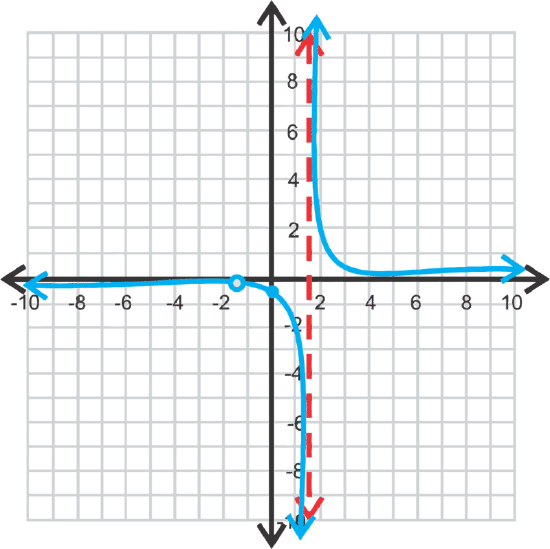
\(\ y=\frac{2 x+3}{6 x^{2}-x-15}\)

Solution

x-intercepts: none, hole at \(\ x=-\frac{3}{2}\)

y-intercept: \(\ \left(0,-\frac{1}{5}\right)\)

horizontal asymptote: y=0

vertical asymptote: \(\ x=\frac{5}{3}\)

f-d_bcaf7e3d7cca8d903e9d9733c8aea81759a9e3d538337153ea5ba5f3+IMAGE_TINY+IMAGE_TINY.png

Review

Find all asymptotes of the following functions.

\(\ y=\frac{x-2}{x^{2}+6 x+8}\)
\(\ y=\frac{x^{2}-4}{x+5}\)
\(\ y=\frac{x^{2}}{x-3}\)
Find the x-intercepts of the function in #2.
Find the x-intercepts of the function in #3.

Graph the following functions. Find any intercepts, asymptote and holes.

\(\ y=\frac{x+1}{x^{2}-x-12}\)
\(\ f(x)=\frac{x^{2}+3 x-10}{x-3}\)
\(\ y=\frac{x-7}{2 x^{2}-11 x-21}\)
\(\ g(x)=\frac{2 x^{2}-2}{3 x+5}\)
\(\ y=\frac{x^{2}+x-30}{x+6}\)
\(\ f(x)=\frac{x^{2}+x-30}{2 x^{3}-5 x^{2}-4 x+3}\)
\(\ y=\frac{x^{3}-2 x^{2}-3 x}{x^{2}-5 x+6}\)
\(\ f(x)=\frac{2 x+5}{x^{2}+5 x-6}\)
\(\ g(x)=\frac{-x^{2}+3 x+4}{2 x-6}\)
Determine the slant asymptote of \(\ y=\frac{3 x^{2}-x-10}{3 x+5}\). Now, graph this function. Is there really a slant asymptote? Can you explain your results?

Answers for Review Problems

To see the Review answers, open this PDF file and look for section 9.6.

Vocabulary

Term	Definition
Slant Asymptote	A slant asymptote is a diagonal line marking a specific range of values toward which the graph of a function may approach, but will never reach. A slant asymptote exists when the numerator of the function is exactly one degree greater than the denominator. A slant asymptote may be found through long division.

Search

Text Color

Text Size

Margin Size

Font Type

Example 1

Example 2

Example 3

Example 4

Example 5

Graphing when the Degrees of the Numerator and Denominator are Different

Graphing Rational Functions

Recap

Examples

Example 1

Example 2

Example 3

Example 4

Example 5

Review

Answers for Review Problems

Vocabulary

Image Attributions