7.3.1: Inductive Reasoning from Patterns
- Page ID
- 14790
Inductive Reasoning from Patterns
Inductive Reasoning
One type of reasoning is inductive reasoning. Inductive reasoning entails making conclusions based upon examples and patterns. Visual patterns and number patterns provide good examples of inductive reasoning. Let’s look at some patterns to get a feel for what inductive reasoning is.
What if you were given a pattern of three numbers or shapes and asked to determine the sixth number or shape that fit that pattern?
Examples
A dot pattern is shown below. How many dots would there be in the 4th figure? How many dots would be in the 6th figure?
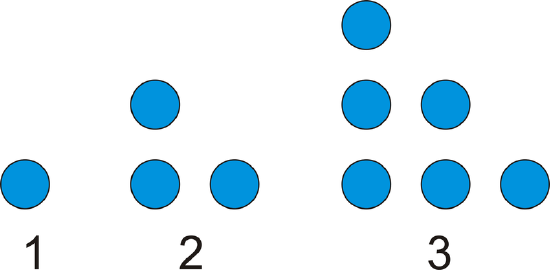
Solution
Draw a picture. Counting the dots, there are \(\ 4+3+2+1=10\) dots.
For the 6th figure, we can use the same pattern, \(\ 6+5+4+3+2+1\). There are 21 dots in the 6th figure.
How many triangles would be in the 10th figure?
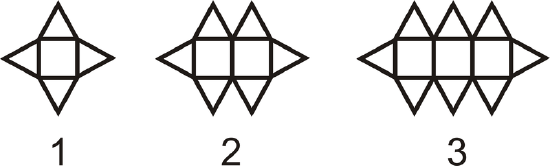
Solution
There would be 10 squares in the 10th figure, with a triangle above and below each one. There is also a triangle on each end of the figure. That makes \(\ 10+10+2=22\) triangles in all.
Look at the pattern 2, 4, 6, 8, 10, … What is the 19th term in the pattern?
Solution
Each term is 2 more than the previous term.
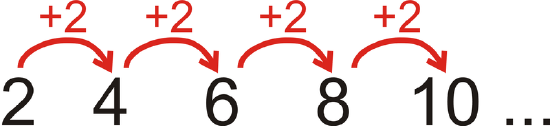
You could count out the pattern until the 19th term, but that could take a while. Notice that the 1st term is 2⋅1, the 2nd term is 2⋅2, the 3rd term is 2⋅3, and so on. So, the 19th term would be 2⋅19 or 38.
Look at the pattern: 3, 6, 12, 24, 48, …
What is the next term in the pattern? What is the 10th term?
Solution
Each term is multiplied by 2 to get the next term.
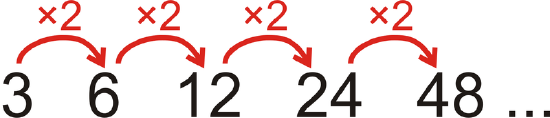
Therefore, the next term will be 48⋅2 or 96.
To find the 10th term, continue to multiply by 2, or \(\ 3 \cdot \underbrace{2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2}_{2^{9}}=1536\)
Find the 8th term in the list of numbers: \(\ \frac{3}{4}, \frac{4}{9}, \frac{5}{16}, \frac{6}{25} \ldots\)
Solution
First, change 2 into a fraction, or \(\ \frac{2}{1}\). So, the pattern is now \(\ \frac{2}{1}, \frac{3}{4}, \frac{4}{9}, \frac{5}{16}, \frac{6}{25} \ldots\) The top is 2, 3, 4, 5, 6. It increases by 1 each time, so the 8th term’s numerator is 9. The denominators are the square numbers, so the 8th term’s denominator is 82 or 64. The 8th term is \(\ \frac{9}{64}\).
Review
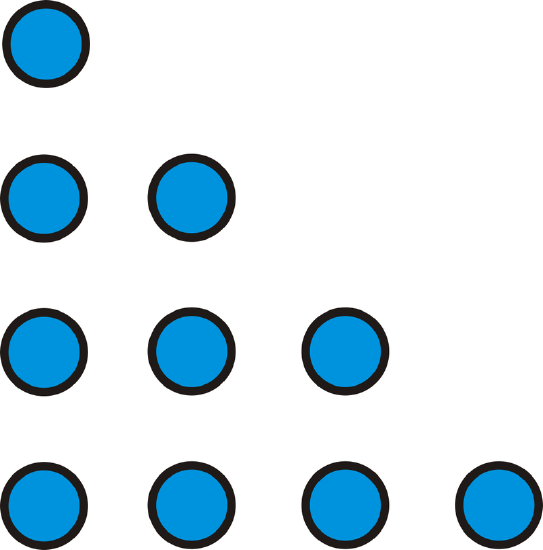
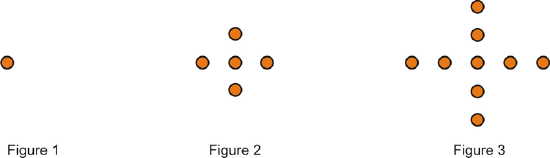
For questions 1-3, determine how many dots there would be in the 4th and the 10th pattern of each figure below.


- Use the pattern below to answer the questions.

- Draw the next figure in the pattern.
- How does the number of points in each star relate to the figure number?
- Use the pattern below to answer the questions. All the triangles are equilateral triangles.
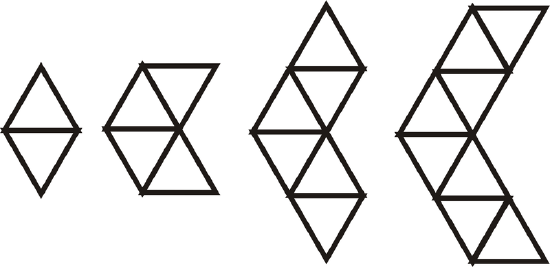
- Draw the next figure in the pattern. How many triangles does it have?
- Determine how many triangles are in the 24th figure.
For questions 6-13, determine: the next three terms in the pattern.
- \(\ 5,8,11,14,17, \ldots\)
- \(\ 6, 1, -4, -9, -14, \ldots\)
- \(\ 2, 4, 8, 16, 32, \ldots\)
- \(\ 67, 56, 45, 34, 23, \ldots\)
- \(\ 9, -4, 6, -8, 3, \ldots\)
- \(\ \frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \frac{5}{6} \ldots\)
- \(\ \frac{2}{3}, \frac{4}{7}, \frac{6}{11}, \frac{8}{15}, \frac{10}{19}, \ldots\)
- \(\ -1,5,-9,13,-17, \ldots\)
For questions 14-17, determine the next two terms and describe the pattern.
- 3, 6, 11, 18, 27, …
- 3, 8, 15, 24, 35, …
- 1, 8, 27, 64, 125, …
- 1, 1, 2, 3, 5, …
Resources
Vocabulary
| Term | Definition |
|---|---|
| Inductive Reasoning | Inductive reasoning is a type of reasoning where one draws conclusions from patterns and previous examples. |
| Equilateral Triangle | An equilateral triangle is a triangle in which all three sides are the same length. |

