7.6.2: Finding the nth Term Given Two Terms for an Arithmetic Sequence
- Page ID
- 14801
Finding the nth Term Given Two Terms
You are paying off a student loan in monthly installments. After your fifth payment your remaining balance on the loan is $17,500. After your 16th payment, your remaining balance is $12,000. What is the nth term rule for the sequence represented by this situation?
Finding the nth Term
Previously, we were given the common difference directly or two consecutive terms from which we could determine the common difference. In this concept we will find the common difference and write nth term rule given any two terms in the sequence.
Let's find the common difference, first term and \(\ n^{t h}\) term rule for the arithmetic sequence in which \(\ a_{7}=17\) and \(\ a_{20}=82\).
We will start by using the \(\ n^{t h}\) term rule for an arithmetic sequence to create two equations in two variables:
\(\ a_{7}=17\), so \(\ a_{1}+(7-1) d=17\) or more simply: \(\ a_{1}+6 d=17\)
\(\ a_{20}=82\), so \(\ a_{1}+(20-1) d=82\) or more simply: \(\ a_{1}+19 d=82\)
Solve the resulting system:
\(\ \begin{array}{r}
a_1 +6d =17 & \not{a_1}+6d =17\\
\underline{-1(a_1+19d=82)}& \quad\quad\Rightarrow \quad\quad\underline{-\not{a_1}-19d=-82}\\
&-13d=-65\\
&d=5\end{array}\)
Replacing \(\ d\) with 5 in one of the equations we get
\(\ \begin{aligned}
a_{1}+6(5) &=7 \\
a_{1}+30 &=17 \\
a_{1} &=-13
\end{aligned}\)
Using these values we can find the nth term rule:
\(\ \begin{array}{l}
a_{n}=-13+(n-1)(5) \\
a_{n}=-13+5 n-5 \\
a_{n}=5 n-18
\end{array}\)
Now, let's find the common difference, first term and \(\ n^{t h}\) term rule for the arithmetic sequence in which \(\ a_{11}=-13\) and \(\ a_{40}=-71\).
Though this is exactly the same type of problem as the previous problem above, we are going to use a different approach. We know that the \(\ n^{t h}\) term rule is really just using the first term and adding \(\ d\) to it \(\ n-1\) times to find the \(\ n^{t h}\) term. We are going to use that idea to find the common difference. To get from the \(\ 11^{t h}\) term to the \(\ 40^{t h}\) term, the common difference is added 40−11 or 29 times. The difference in the term values is −71−(−13) or -58. What must be added 29 times to create a difference of -58? We can subtract the terms and divide by the difference in term number to determine the common difference.
\(\ \frac{-71-(-13)}{40-11}=\frac{-71+13}{29}=\frac{-58}{29}=-2 . \text { So } d=-2\)
Now we can use the common difference and one of the terms to find the first term as we did previously.
\(\ \begin{aligned}
a_{1}+(11-1)(-2) &=-13 \\
a_{1}+(-20) &=-13 \\
a_{1} &=7
\end{aligned}\)
Writing the \(\ n^{t h}\) term rule we get: \(\ a_{n}=7+(n-1)(-2)=7-2 n+2=-2 n+9\).
Before we look at the next problem for this concept, we are going to connect the \(\ n^{t h}\) term rule for an arithmetic sequence to the equation of a line. Have you noticed that the simplified \(\ n^{t h}\) term rule, \(\ a_{n}=p n+q\), where \(\ p\) and \(\ q\) represent constants, looks a little like \(\ y=m x+b\), the slope-intercept form of the equation of a line? Let’s explore why this is the case using the arithmetic sequence 1, 4, 7, 10, … If we create points by letting the x – coordinate be the term number and the y – coordinate be the term, we get the following points and can plot them in the coordinate plane as shown below,
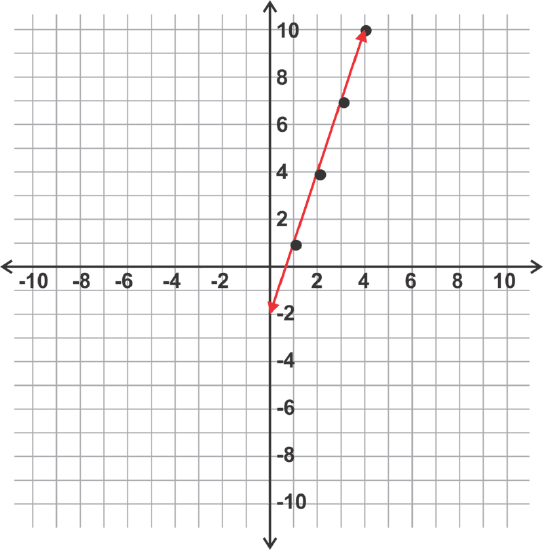
The points are: (1, 1), (2, 4), (3, 7), (4, 10)
Notice, that all of these points lie on the same line. This happens because for each increase of one in the term number (x), the term value (y) increases by 3. This common difference is actually the slope of the line.
We can find the equation of this line using the slope, 3, and the point (1, 1) in the equation \(\ y=m x+b\) as follows:
\(\ \begin{aligned}
1&=3(1)+b\\
1&=2+b \quad \text { , so the equation of the line is } y=3 x-1\\
-1&=b
\end{aligned}\)
The \(\ n^{t h}\) term rule for the sequence is thus: \(\ a_{n}=3 n-1\).
Finally, let's find the common difference, first term and \(\ n^{t h}\) term rule for the arithmetic sequence in which \(\ a_{10}=-50\) and \(\ a_{32}=-182\).
This time we will use the concept that the terms in an arithmetic sequence are actually points on a line to write an equation. In this case our points are (10, −50) and (32, −182). We can find the slope and the equation as shown.
\(\ m=\frac{-182-(-50)}{32-10}=\frac{-132}{22}=-6\)
Use the point (10, −50) so find the y-intercept:
\(\ \begin{aligned}
-50 &=-6(10)+b \\
-50 &=-60+b \\
10 &=b
\end{aligned}\)
So \(\ y=-6 x+10\) and \(\ a_{n}=-6 n+10\).
Examples
Earlier, you were asked to find the \(\ n^{t h}\) term rule for the sequence represented by the student loan situation.
Solution
In this case our points are (5, 17, 500) and (16, 12, 000). We can find the slope and the equation as shown.
\(\ m=\frac{12,000-17,500}{16-5}=\frac{-5500}{11}=-500\)
Use the point (5, 17, 500) to find the y-intercept:
\(\ \begin{array}{l}
17,500=-500(5)+b \\
17,500=-2500+b \\
20,000=b
\end{array}\)
So \(\ y=-500 x+20,000\) and \(\ a_{n}=-500 n+20,000\).
Find the \(\ n^{t h}\) term rule for the arithmetic sequence with \(\ a_{6}=-13\) and \(\ a_{15}=-40\).
Solution
From \(\ a_{6}=-13\) we get the equation \(\ a_{1}+(6-1) d=a_{1}+5 d=-13\).
From \(\ a_{15}=-40\) we get the equation \(\ a_{1}+(15-1) d=a_{1}+14 d=-40\).
Use the two equations to solve for \(\ a_{1}\) and \(\ d\):
\(\ \begin{array}{r}
a_1+5d=-13& a_1+5(-3)=-13\\
\underline{-a_1-14d=40}& \text{ Used } d \text{ to find } a_1 \Rightarrow \quad\quad\quad a_1-15=-13\\
-9d=17 & a_1=2\\
d=-3
\end{array}\)
Find the \(\ n^{t h}\) term rule: \(\ a_{n}=2+(n-1)(-3)=2-3 n+3=-3 n+5\).
Find the \(\ n^{t h}\) term rule for the arithmetic sequence with \(\ a_{6}=13\) and \(\ a_{22}=77\).
Solution
The common difference is \(\ \frac{77-13}{22-6}=\frac{64}{16}=4\). The first term can be found using \(\ a_{6}=13\):
\(\ \begin{aligned}
a_{1}+(6-1)(4) &=13 \\
a_{1}+20 &=13 \\
a_{1} &=-7
\end{aligned}\)
Thus \(\ a_{n}=-7+(n-1)(4)=-7+4 n-4=4 n-11\).
Find the \(\ n^{t h}\) term rule for the arithmetic sequence with \(\ a_{7}=-75\) and \(\ a_{25}=-273\).
Solution
From \(\ a_{7}=-75\) we get the point \(\ (7,-75)\). From \(\ a_{25}=-273\) we get the point \(\ (25,-273)\).
The slope between these points is \(\ \frac{-273-(-75)}{25-7}=\frac{-198}{18}=-11\)
The y-intercept can be found next using the point \(\ (7,-75)\):
\(\ \begin{aligned}
-75 &=-11(7)+b \\
-75 &=-77+b \\
2 &=b
\end{aligned}\)
The final equation is \(\ y=-11 x+2\) and the \(\ n^{t h}\) term rule is \(\ a_{n}=-11 n+2\).
Review
Use the two given terms to find an \(\ n^{t h}\) term rule for the sequence.
- \(\ a_{7}=-17\) and \(\ a_{25}=-71\)
- \(\ a_{11}=23\) and \(\ a_{42}=85\)
- \(\ a_{3}=-6\) and \(\ a_{12}=-3\)
- \(\ a_{8}=24\) and \(\ a_{2}=9\)
- \(\ a_{6}=-27\) and \(\ a_{10}=-47\)
- \(\ a_{4}=37\) and \(\ a_{12}=85\)
- \(\ a_{13}=-20\) and \(\ a_{30}=-54\)
- \(\ a_{3}=23\) and \(\ a_{9}=65\)
- \(\ a_{30}=-31\) and \(\ a_{45}=-46\)
- \(\ a_{5}=25\) and \(\ a_{11}=73\)
- \(\ a_{10}=-2\) and \(\ a_{25}=-14\)
- \(\ a_{16}=14\) and \(\ a_{28}=23\)
- \(\ a_{2}=4 n+3\) and \(\ a_{19}=4 n+65\)
- \(\ a_{10}=-3 n+7\) and \(\ a_{23}=-3 n-16\)
- Which method do you prefer? Why?
Answers for Review Problems
To see the Review answers, open this PDF file and look for section 11.6.

