8.2.1: Tangents to a Curve
- Page ID
- 14817
Tangents to a Curve
Kevin is learning about the basis of calculus and what calculus is actually used for. Unfortunately, Kevin does not understand why calculus is sometimes necessary to find the equation of a line. In Algebra 1, he learned you can find the equation of a line if you are given two points. You find the slope of the line by dividing the up/down difference in the points by the left/right difference, then you use one of the points and the slope to find the y-intercept.
Kevin's teacher, Mr. Banner, offered him extra credit if he could find the slope of a line for the points (4,5) and (4,5) using the method he learned in Algebra 1. Can you see what Mr. Banner did? What is Kevin going to find as he works on those problems?
Tangents to a Curve
Recall from algebra, if points \(\ P\left(x_{0}, y_{0}\right)\) and \(\ Q\left(x_{1}, y_{1}\right)\) are two different points on the curve \(\ y=f(x)\), then the slope of the secant line connecting the two points is given by
| \(\ m_{s e c}=\frac{y_{1}-y_{0}}{x_{1}-x_{0}}=\frac{f\left(x_{1}\right)-f\left(x_{0}\right)}{x_{1}-x_{0}} \tag{1}\) |
|---|
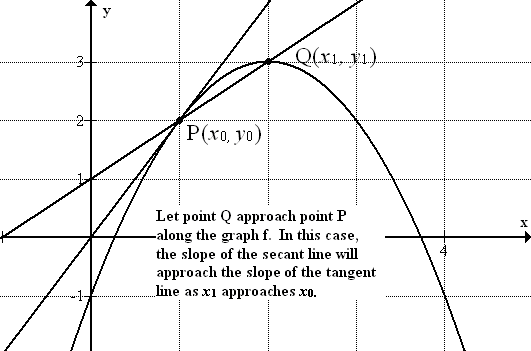
Of course, if we let the point x1 approach xo then Q will approach P along the graph f and thus the slope of the secant line will gradually approach the slope of the tangent line as x1 approaches x0. Therefore, (1) becomes
| \(\ m_{s e c}=\lim _{x_{1} \rightarrow x_{0}} \frac{f\left(x_{1}\right)-f\left(x_{0}\right)}{x_{1}-x_{0}} \tag{2}\) |
|---|
To simplify our notation, if we let h = x1 −x0, then x1 = x0 + h and x1 → x0 becomes equivalent to h → 0. This means that (2) becomes
| \(\ m_{s e c}=\lim _{h \rightarrow 0} \frac{f\left(x_{0}+h\right)-f\left(x_{0}\right)}{h}\) |
|---|
|
The Slope of a Tangent Line
provided that the limit exist. |
|---|
Recall that the equation of the tangent line through point (x0, y0) with slope m is the point-slope form of a line: y − y0 = mtan(x − x0).
Examples
Earlier, you were given a problem about Kevin, who is having trouble understanding calculus.
Solution
Mr. Banner asked Kevin to find the equation of a line given the points (4, 5) and (4, 5). The points (4, 5) and (4, 5) are the same, so the \(\ \frac{\text { rise }}{\text { run }}\) would be \(\ \frac{0}{0}\) - Kevin was just introduced to the need for differential calculus!
Find line tangent to the curve \(\ f(x)=x^{3}\) that passes through point P (2, 8).
Solution
Since P(x0, y0) = (2, 8), using the slope of the tangent equation we have
| mtan | \(\ m_{t a n}=\lim _{h \rightarrow 0} \frac{f\left(x_{0}+h\right)-f\left(x_{0}\right)}{h}\) | |
|---|---|---|
| and we get | ||
| mtan | \(\ =\lim _{h \rightarrow 0} \frac{f(2+h)-f(2)}{h}\) | |
| \(\ =\lim _{h \rightarrow 0} \frac{\left(h^{3}+6 h^{2}+12 h+8\right)-8}{h}\) | ||
| \(\ =\lim _{h \rightarrow 0} \frac{h^{3}+6 h^{2}+12 h}{h}\) | ||
| \(\ =\lim _{h \rightarrow 0}\left(h^{2}+6 h+12\right)\) | ||
| \(\ =12\) |
Thus the slope of the tangent line is \(\ 12\). Using the point-slope formula above, we find that the equation of the tangent line is \(\ y-8=12(x-2)\) or \(\ y=12 x-16\).
If \(\ f(x)=x^{2}-3\), find \(\ f^{\prime}(x)\) and use the result to find the slope of the tangent line at \(\ x = 2\) and \(\ x = −1\).
Solution
Since \(\ f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\) then
| \(\ f^{\prime}(x)\) | \(\ =\lim _{h \rightarrow 0} \frac{\left[(x+h)^{2}-3\right]-\left[x^{2}-3\right]}{h}\) |
|---|---|
| \(\ =\lim _{h \rightarrow 0} \frac{x^{2}+2 x h+h^{2}-3-x^{2}+3}{h}\) | |
| \(\ =\lim _{h \rightarrow 0} \frac{2 x h+h^{2}}{h}\) | |
| \(\ =\lim _{h \rightarrow 0}(2 x+h)\) | |
| \(\ =2x\) |
To find the slope, we simply substitute \(\ x = 2\) into the result \(\ f^{\prime}(x)\):
| f'(x) | = 2x | |
|---|---|---|
| f'(2) | = 2(2) | |
| = 4 | ||
| and | ||
| f'(x) | = 2x | |
| f'(-1) | = 2(-1) | |
| = -2 |
Thus slope of the tangent line at x = 2 and x = −1 are 4 and −2 respectively.
Find the slope of the tangent line to the curve \(\ y=1 / x\) that passes through the point (1, 1).
Solution
Using the slope of the tangent formula,
| \(\ f^{\prime}(x)\) | \(\ =\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\) | ||
|---|---|---|---|
| and substituting \(\ y=\frac{1}{x}\) | |||
| \(\ f^{\prime}(x)\) | \(\ =\lim _{h \rightarrow 0} \frac{\left(\frac{1}{x+h}\right)-\frac{1}{x}}{h}\) | ||
| \(\ =\lim _{h \rightarrow 0} \frac{\frac{x-x-h}{x(x+h)}}{h}\) | |||
| \(\ =\lim _{h \rightarrow 0} \frac{x-x-h}{h x(x+h)}\) | |||
| \(\ =\lim _{h \rightarrow 0} \frac{-1}{x(x+h)}\) | |||
| \(\ =\lim _{h \rightarrow 0} \frac{-1}{x(x+h)}\) | |||
| \(\ =\frac{-1}{x^{2}}\) | |||
| For \(\ x = 1\), the slope is | |||
| \(\ f^{\prime}(x)\) | \(\ =\frac{-1}{1}=-1\) | ||
| \(\ =−1\) |
Thus the slope of the tangent line at \(\ x = 1\) for the curve \(\ y=1 / x\) is \(\ m=-1\). To find the equation of the tangent line, we simply use the point-slope formula,
| y - y0 | = m(x - x0) | ||
|---|---|---|---|
| Where (x0, y0) = (1, 1). | |||
| y - 1 | = -1(x - 1) | ||
| y | = -x + 1 + 1 | ||
| y | = -x + 2 |
So the equation of the tangent line is y = -x + 2.
Given the function \(\ y=\frac{1}{2} x^{2}\) and the values of \(\ x_{0}=3\) and \(\ x_{1}=4\), find:
- The average rate of change of y with respect to x over the interval [x0, x1].
- The slope of the secant line connecting x0 and x1.
- The instantaneous rate of change of y with respect to x at x0.
- The slope of the tangent line at x1.
Solution
- Identify the two points by substituting 3 and 4 in for \(\ x\) in the function \(\ f(x)=\frac{1}{2} x^{2}\)
Substitute the two points (3, 4.5) and (4, 8) into the average rate of change formula: \(\ m=\frac{y_{1}-y_{0}}{x_{1}-x_{0}}\)
Average rate of change \(\ =\frac{7}{2}\)
- The slope of the secant line between x0 and x1 is the slope between (3, 4.5) and (4, 8), which is \(\ \frac{7}{2}\).
- Instantaneous rate of change is the slope at \(\ x = 3\).
Use the formula: \(\ \frac{f(x+h)-f(x)}{h}\) where \(\ f(x)=\frac{1}{2} x^{2}\) and \(\ x=3\)
\(\ \frac{f(3+h)-f(3)}{h}\)... Substitute \(\ 3\) for \(\ x\)
\(\ \frac{\frac{1}{2}(3+h)^{2}-\frac{1}{2}(3)^{2}}{h}\)... Replace \(\ f(x) \rightarrow \frac{1}{2} x^{2}\)
\(\ \frac{\frac{1}{2}(9)+\frac{1}{2}(6 h)+\frac{1}{2} h^{2}-\frac{1}{2} 9}{h}\)... FOIL and Distribute the 1/2
\(\ \frac{6 h+h^{2}}{2 h}\)... Simplify
\(\ 3+\frac{h}{2}\)... Simplify again
\(\ 3\)... As \(\ h \rightarrow 0\)
∴ the instantaneous slope at \(\ x = 3\) is \(\ 3\)
- The slope of the tangent at 4 is the same as the instantaneous rate of change at \(\ x=4\)
This is the same series of steps as with \(\ x = 3\) above
∴ the slope at \(\ x = 4\) is \(\ 4\)
Given the function \(\ f(x)=\frac{1}{x}\) and the values \(\ x_{0}=2\) and \(\ x_{1}=3\), find:
- The average rate of change of y with respect to x over the interval [x0, x1].
- The slope of the secant line connecting x0 and x1.
- The instantaneous rate of change of y with respect to x at x0.
- The slope of the tangent line at x1.
Solution
- Identify the two points by substituting 2 and 3 in for x in the function \(\ f(x)=\frac{1}{x}\) to get \(\ \left(2, \frac{1}{2}\right) \mid\left(3, \frac{1}{3}\right)\)
Substitute the two points \(\ \left(2, \frac{1}{2}\right) \mid\left(3, \frac{1}{3}\right)\) into the average rate of change formula: \(\ m=\frac{y_{1}-y_{0}}{x_{1}-x_{0}}\)
Average rate of change \(\ =\frac{-1}{6}\)
- The slope of the secant line between \(\ x_{0}\) and \(\ x_{1}\) is the slope between \(\ \left(2, \frac{1}{2}\right)\) and \(\ \left(3, \frac{1}{3}\right)\), which is \(\ \frac{-1}{6}\).
- Instantaneous rate of change at \(\ x_{0}\) is the slope at \(\ x= 2\).
Use the formula: \(\ \frac{f(x+h)-f(x)}{h}\) where \(\ f(x)=\frac{1}{x}\) and \(\ x=2\)
\(\ \frac{f(2+h)-f(2)}{h}\)... Substitute \(\ 2\) for \(\ x\)
\(\ \frac{\frac{1}{2+h}-\frac{1}{2}}{h}\)... Replace \(\ f(x) \rightarrow \frac{1}{x}\)
\(\ \left(\frac{1}{2+h}-\frac{1}{2}\right) \cdot \frac{1}{h}\)... We had a fraction divided by a fraction, invert to multiply
\(\ \frac{(2)(1)}{2(2+h)}-\frac{(2+h)(1)}{2(2+h)} \cdot \frac{1}{h}\)... Set common denominators
\(\ \frac{(2)-(2+h)}{(2+h)(2)(h)}\)... Simplify
\(\ \frac{-h}{4 h+2 h^{2}}\)... Simplify again
\(\ \frac{-1}{4+2 h}\)... once more (canceling the \(\ h\))
\(\ \frac{-1}{4}\)... As \(\ h \rightarrow 0\)
∴ the instantaneous slope at \(\ x=2\) is \(\ \frac{-1}{4}\)
- The slope of the tangent at 3 is the same as the instantaneous rate of change at \(\ x=3\)
This is the same series of steps as with \(\ x = 2\) above
∴ the slope at \(\ x = 3\) is \(\ \frac{-1}{9}\)
Review
- What is the line connecting two points \(\ \left(x_{0}, y_{0}\right)\) and \(\ \left(x_{1}, y_{1}\right)\) on a curve called?
- As \(\ \left(x_{0}, y_{0}\right)\) gets immeasurably close to \(\ \left(x_{1}, y_{1}\right)\) the term describing the line between them becomes: "the ____________ line"
- The expression \(\ f\left(x_{0}+h\right)-f\left(x_{0}\right)\) is used to describe what distance in the process of finding the slope of a tangent line?
- When calculating the slope of a tangent, what value is assumed to go to 0 as the two chosen points get closer and closer?
- What does the concept of limit, discussed in prior lessons, have to do with finding the slope of a line tangent to a curve?
Find the equation of the tangent line:
- What is the equation of the tangent line at \(\ x=−3\) assuming that \(\ r(-3)=-5\) and \(\ r^{\prime}(-3)=1\)?
- What is the equation of the tangent line at \(\ x=1\) assuming that \(\ r(1)=3\) and \(\ r^{\prime}(1)=-5\)?
- What is the equation of the tangent line at \(\ x=2\) assuming that \(\ g(2)=1\) and \(\ g^{\prime}(2)=-3\)?
- What is the equation of the tangent line at \(\ x=4\) assuming that \(\ u(4)=4\) and \(\ u^{\prime}(4)=3\)?
- What is the equation of the tangent line at \(\ x=-4\) assuming that \(\ t(-4)=2\) and \(\ t^{\prime}(-4)=5\)?
Find the equation of the tangent line:
- Find the equation of the tangent line to the graph of \(\ h(x)=-5 x^{3}-3 x^{2}+x+3\) at \(\ x=1\)
- Find the equation of the tangent line to the graph of \(\ t(x)=-2 x\) at \(\ x=-2\)
- Find the equation of the tangent line to the graph of \(\ m(x)=3 x^{3}+3 x^{2}+4 x+4\) at \(\ x=1\)
- Find the equation of the tangent line to the graph of \(\ q(x)=-x^{3}-4 x^{2}+4 x+3\) at \(\ x=−2\)
- Find the equation of the tangent line to the graph of \(\ t(x)=-4 x^{2}+2 x-4\) at \(\ x=−1\)
- Find the equation of the tangent line to the graph of \(\ h(x)=-4 x^{3}+2 x^{2}-3 x+3\) at \(\ x=−1\)
- Find the equation of the tangent line to the graph of \(\ m(x)=x\) at \(\ x=0\)
- Find the equation of the tangent line to the graph of \(\ s(x)=-3 x^{2}-2 x+3\) at \(\ x=0\)
- Find the equation of the tangent line to the graph of \(\ c(x)=-3\) at \(\ x=0\)
- Find the equation of the tangent line to the graph of \(\ b(x)=-5 x^{4}+3 x^{3}-x^{2}+5 x-3\) at \(\ x=−1\).
Vocabulary
| Term | Definition |
|---|---|
| secant | A line that intersects a circle in two points. |
| tangent | A line that intersects a circle in exactly one point. |
| Average rate of change | The average rate of change of a function is the change in y coordinates of a function, divided by the change in x coordinates. |
| Differential calculus | Differential calculus is the branch of calculus based on finding the difference in location between two points that get closer together until the distance between them is infinitely small. |
| instantaneous rate of change | The instantaneous rate of change of a curve at a given point is the slope of the line tangent to the curve at that point. |
| secant line | A secant line is a line that joins two points on a curve. |
| Slope | Slope is a measure of the steepness of a line. A line can have positive, negative, zero (horizontal), or undefined (vertical) slope. The slope of a line can be found by calculating “rise over run” or “the change in the y over the change in the x.” The symbol for slope is m |
| Tangent line | A tangent line is a line that "just touches" a curve at a single point and no others. |

