2.2.2: Graphs of Polynomials Using Zeros
- Page ID
- 14193
Graphs of Polynomials Using Zeros
How is finding and using the zeroes of a higher-degree polynomial related to the same process you have used in the past on quadratic functions?
Graphing Polynomials Using Zeros
The following procedure can be followed when graphing a polynomial function.
- Use the leading-term test to determine the end behavior of the graph.
- Find the x−intercept(s) of f(x) by setting f(x)=0 and then solving for x.
- Find the y−intercept of f(x) by setting y=f(0) and finding y.
- Use the x−intercept(s) to divide the x−axis into intervals and then choose test points to determine the sign of f(x) on each interval.
- Plot the test points.
- If necessary, find additional points to determine the general shape of the graph.
The Leading-Term Test
If anxn is the leading term of a polynomial. Then the behavior of the graph as x→∞ or x→−∞ can be known by one the four following behaviors:
2. If an<0 and n even: 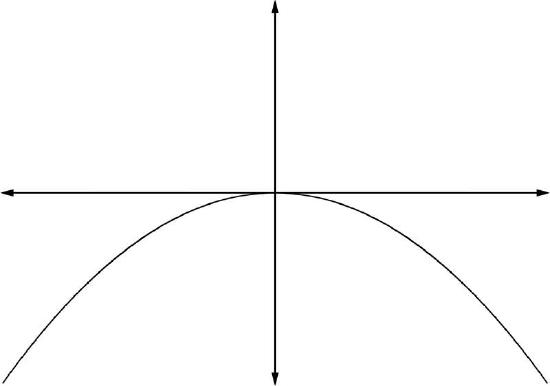
3. If an>0 and n odd: 
4. If an<0 and n odd: 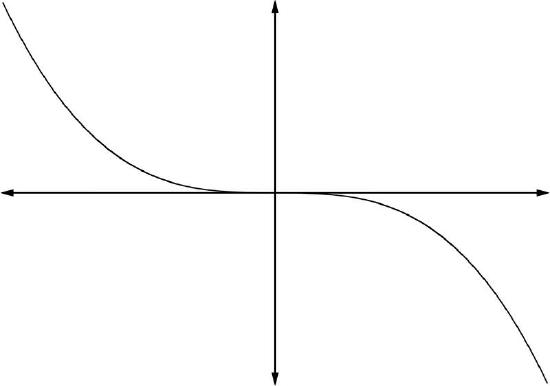
Examples
Earlier, you were asked to identify some similarities in graphing using zeroes between quadratic functions and higher-degree polynomials.
Solution
Despite the more complex nature of the graphs of higher-degree polynomials, the general process of graphing using zeroes is actually very similar. In both cases, your goal is to locate the points where the graph crosses the x or y axis. In both cases, this is done by setting the y value equal to zero and solving for x to find the x axis intercepts, and setting the x value equal to zero and solving for y to find the y axis intercepts.
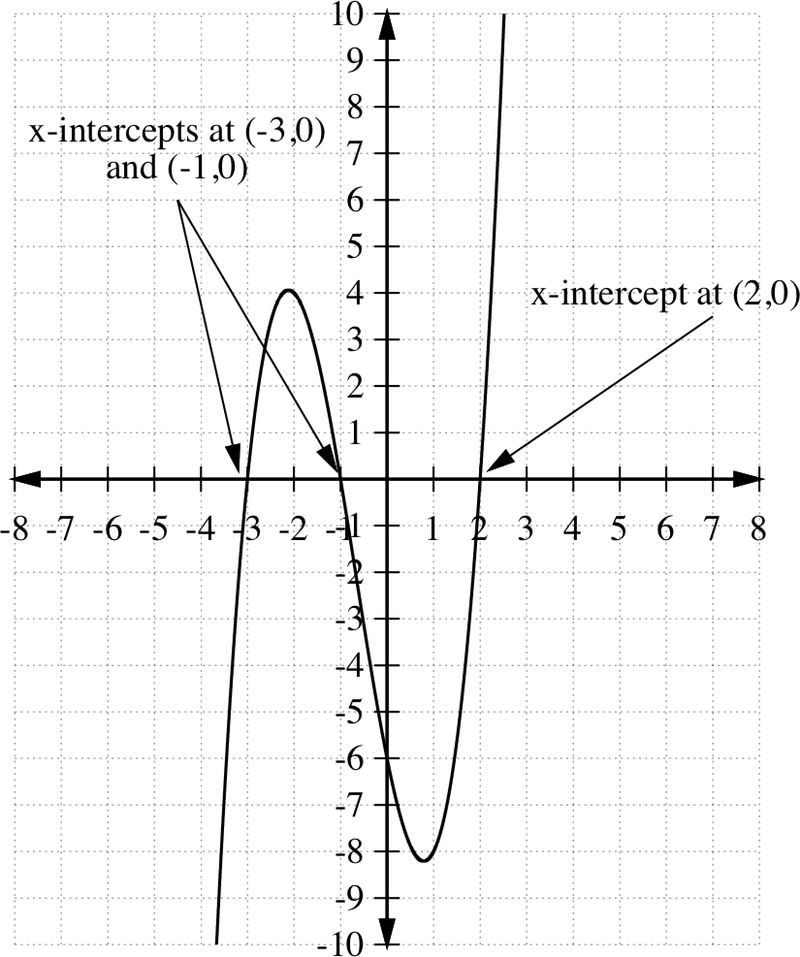
Find the roots (zeroes) of the polynomial:
h(x)=x3+2x2−5x−6
Solution
Start by factoring:
h(x)=x3+2x2−5x−6=(x+1)(x−2)(x+3)
To find the zeros, set h(x)=0 and solve for x.
(x+1)(x−2)(x+3)=0
This gives
x+1=0
x−2=0
x+3=0
or
x=-1
x=2
x=-3
So we say that the solution set is {−3,−1,2}. They are the zeros of the function h(x). The zeros of h(x) are the x−intercepts of the graph y=h(x) below.
Find the zeros of g(x)=−(x−2)(x−2)(x+1)(x+5)(x+5)(x+5).
Solution
The polynomial can be written as
g(x)=−(x−2)2(x+1)(x+5)3
To solve the equation, we simply set it equal to zero
−(x−2)2(x+1)(x+5)3=0
this gives
x−2=0
x+1=0
x+5=0
or
x=2
x=-1
x=-5
Notice the occurrence of the zeros in the function. The factor (x−2) occurred twice (because it was squared), the factor (x+1) occurred once and the factor (x+5) occurred three times. We say that the zero we obtain from the factor (x−2) has a multiplicity k=2 and the factor (x+5) has a multiplicity k=3.
Graph the polynomial function f(x)=−3x4+2x3.
Solution
Since the leading term here is −3x4 then an=−3<0, and n=4 even. Thus the end behavior of the graph as x→∞ and x→−∞ is that of Box #2, item 2.
We can find the zeros of the function by simply setting f(x)=0 and then solving for x.
−3x4+2x3=0
−x3(3x−2)=0
This gives
x=0 or x=\(\ 2\over 3\)
So we have two x−intercepts, at x=0 and at x=\(\ 2\over 3\), with multiplicity k=3 for x=0 and multiplicity k=1 for x=\(\ 2\over 3\)
To find the y−intercept, we find f(0), which gives
f(0)=0
So the graph passes the y−axis at y=0.
Since the x−intercepts are 0 and \(\ 2\over 3\), they divide the x−axis into three intervals: (−∞, 0), (0, \(\ 2\over 3\)), and (\(\ 2\over 3\), ∞). Now we are interested in determining at which intervals the function f(x) is negative and at which intervals it is positive. To do so, we construct a table and choose a test value for x from each interval and find the corresponding f(x) at that value.
| Interval | Test Value x | f(x) | Sign of f(x) | Location of points on the graph |
|---|---|---|---|---|
| (−∞, 0) | -1 | -5 | - | below the x−axis |
| (0, \(\ 2\over 3\)) | \(\ 1\over 2\) | \(\ 1\over 16\) | + | above the x−axis |
| (\(\ 2\over 3\), ∞) | 1 | -1 | - | below the x−axis |
Those test points give us three additional points to plot: (−1, −5), (\(\ 1\over 2\), \(\ 1\over 16\)), and (1, -1). Now we are ready to plot our graph. We have a total of three intercept points, in addition to the three test points. We also know how the graph is behaving as x→−∞ and x→+∞. This information is usually enough to make a rough sketch of the graph. If we need additional points, we can simply select more points to complete the graph.
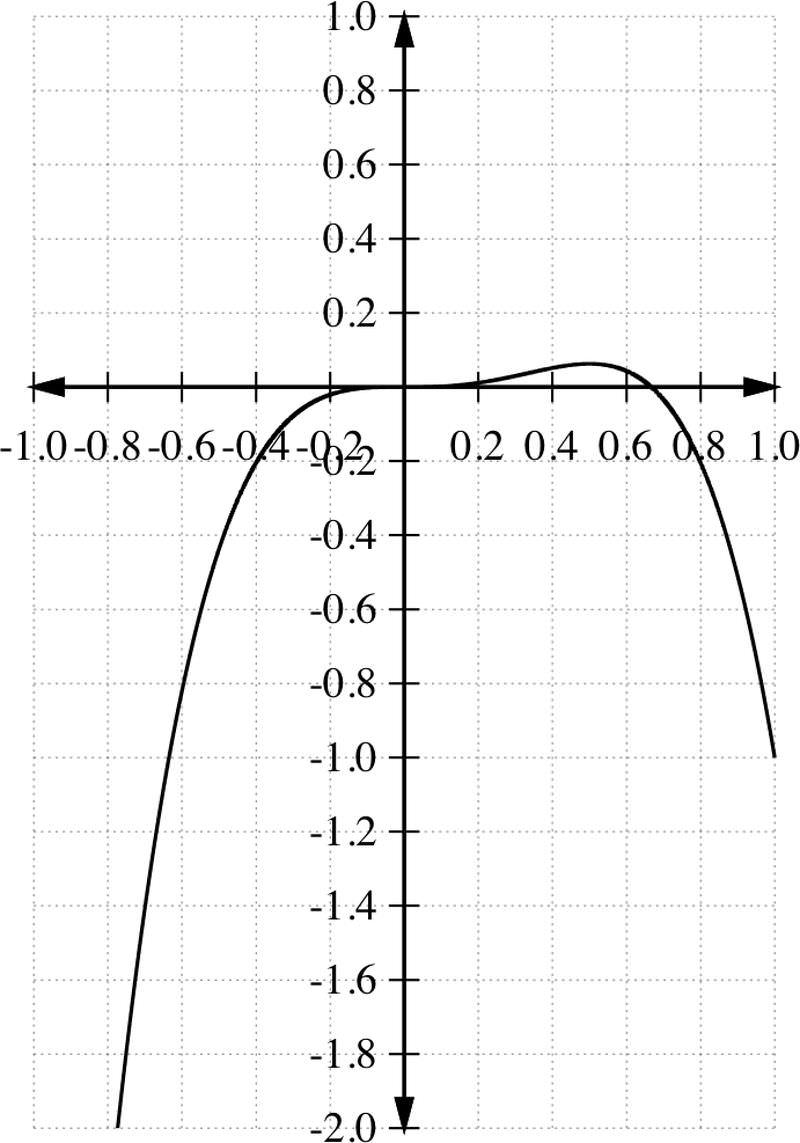
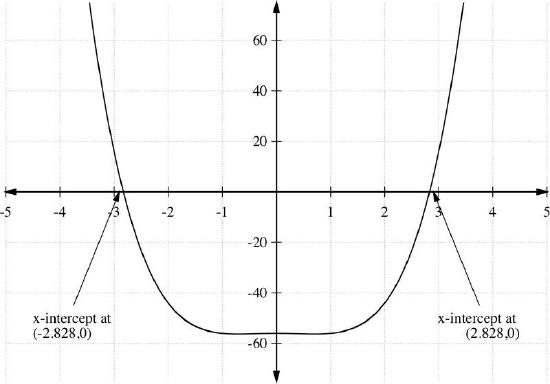
Find the zeros and sketch a graph of the polynomial
f(x)=x4−x2−56
Solution
This is a factorable equation,
f(x)=x4−x2−56
=(x2−8)(x2+7)
Setting f(x)=0,
(x2−8)(x2+7)=0
the first term gives
x2−8=0
x2=0
x= ±\(\ \sqrt{8}\)
= ±\(\ 2\sqrt{2}\)
and the second term gives
x2+7=0
x2=−7
x=±\(\ \sqrt{-7}\)
=±\(\ i\sqrt{7}\)
So the solutions are ±\(\ 2\sqrt{2}\) and ±\(\ i\sqrt{7}\), a total of four zeros of f(x). Keep in mind that only the real zeros of a function correspond to the x−intercept of its graph.
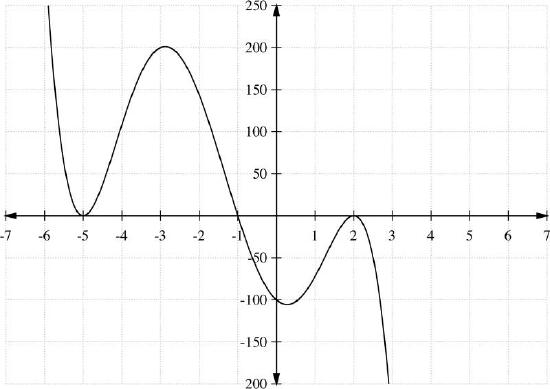
Graph g(x)=−(x−2)2(x+1)(x+5)3.
Solution
Use the zeros to create a table of intervals and see whether the function is above or below the x−axis in each interval:
| Interval | Test value x | g(x) | Sign of g(x) | Location of graph relative to x−axis |
|---|---|---|---|---|
| (−∞, −5) | -6 | 320 | + | Above |
| x=−5 | -5 | 0 | NA | |
| (-5, -1) | -2 | 144 | + | Above |
| x=−1 | -1 | 0 | NA | |
| (-1, 2) | 0 | -100 | - | Below |
| x=2 | 2 | 0 | NA | |
| (2, ∞) | 3 | -256 | - | Below |
Finally, use this information and the test points to sketch a graph of g(x).
Review
- If c is a zero of f, then c is a/an _________________________ of the graph of f.
- If c is a zero of f, then (x - c) is a factor of ___________________?
- Find the zeros of the polynomial: P(x)=x3−5x2+6x
Consider the function: f(x)=−3(x−3)4(5x−2)(2x−1)3(4−x)2.
- How many zeros (x-intercepts) are there?
- What is the leading term?
Find the zeros and graph the polynomial. Be sure to label the x-intercepts, y-intercept (if possible) and have correct end behavior. You may use technology for questions 9-12.
- P(x)=−2(x+1)2(x−3)
- P(x)=x3+3x2−4x−12
- f(x)=−2x3+6x2+9x+6
- f(x)=−4x2−7x+3
- f(x)=2x5+4x3+8x2+6x
- f(x)=x4−3x2
- g(x)=x2−|x|
- Given: P(x)=(3x+2)(x−7)2(9x+2)3
State:
- The leading term:
- The degree of the polynomial:
- The leading coefficient:
Determine the equation of the polynomial based on the graph:
Vocabulary
| Term | Definition |
|---|---|
| Cubic Function | A cubic function is a function containing an x3 term as the highest power of x. |
| Intercept | The intercepts of a curve are the locations where the curve intersects the x and y axes. An x intercept is a point at which the curve intersects the x-axis. A y intercept is a point at which the curve intersects the y-axis. |
| interval | An interval is a specific and limited part of a function. |
| Leading-Term Test | The leading-term test is a test to determine the end behavior of a polynomial function. |
| Polynomial | A polynomial is an expression with at least one algebraic term, but which does not indicate division by a variable or contain variables with fractional exponents. |
| Polynomial Graph | A polynomial graph is the graph of a polynomial function. The term is most commonly used for polynomial functions with a degree of at least three. |
| Quartic Function | A quartic function is a function f(x) containing an x4 term as the highest power of ''x''. |
| Roots | The roots of a function are the values of x that make y equal to zero. |
| Zeroes | The zeroes of a function f(x) are the values of x that cause f(x) to be equal to zero. |