6.4.1: Circles Centered at the Origin

Last updated
Save as PDF

Page ID: 14764

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Circles Centered at the Origin

You draw a circle that is centered at the origin. You measure the diameter of the circle to be 32 units. Does the point \(\ (14,8)\) lie on the circle?

Circles Centered at the Origin

Until now, your only reference to circles was from geometry. A circle is the set of points that are equidistant (the radius) from a given point (the center). A line segment that passes through the center and has endpoints on the circle is a diameter.

Now, we will take a circle and place it on the x−y plane to see if we can find its equation. In this concept, we are going to place the center of the circle on the origin.

Finding the Equation of a Circle

Step 1: On a piece of graph paper, draw an x−y plane. Using a compass, draw a circle, centered at the origin that has a radius of 5. Find the point (3,4) on the circle and draw a right triangle with the radius as the hypotenuse.

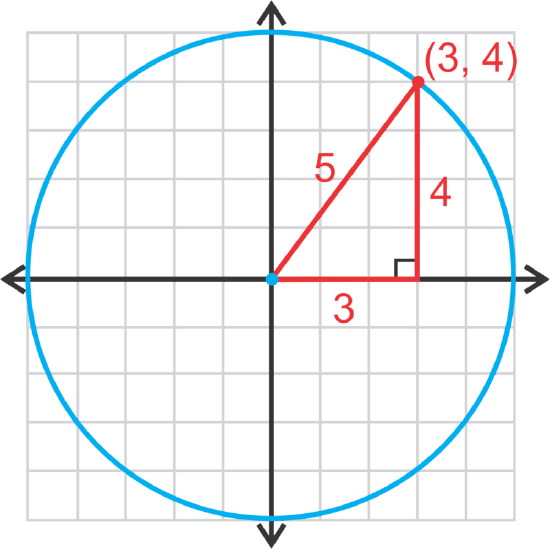
f-d_a422e8f58ba330c8e20238ba1f5fef24d986635c1b5a67f1a4482273+IMAGE_TINY+IMAGE_TINY.png

Step 2: Using the length of each side of the right triangle, show that the Pythagorean Theorem is true.

Step 3: Now, instead of using (3, 4), change the point to (x, y) so that it represents any point on the circle. Using r to represent the radius, rewrite the Pythagorean Theorem.

The equation of a circle, centered at the origin, is \(\ x^{2}+y^{2}=r^{2}\), where r is the radius and (x, y) is any point on the circle.

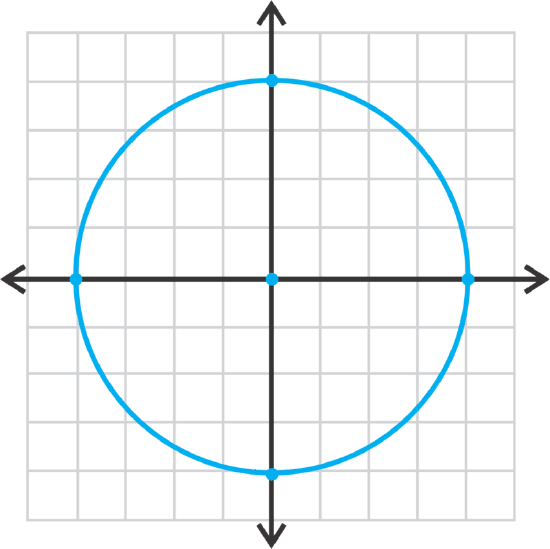
Let's find the radius of \(\ x^{2}+y^{2}=16\) and graph.

To find the radius, we can set \(\ 16=r^{2}\), making \(\ r=4\). \(\ r\) is not -4 because it is a distance and distances are always positive. To graph the circle, start at the origin and go out 4 units in each direction and connect.

f-d_3e19a8efdc4f45e7e77b0ffd27456e06d7f6a32c875d2d748e7bc293+IMAGE_TINY+IMAGE_TINY.png

Now, let's find the equation of the circle with center at the origin and passes through \(\ (−7,−7)\).

Using the equation of the circle, we have: \(\ (-7)^{2}+(-7)^{2}=r^{2}\). Solve for \(\ r^{2}\).

\(\ \begin{aligned}
(-7)^{2}+(-7)^{2} &=r^{2} \\
49+49 &=r^{2} \\
98 &=r^{2}
\end{aligned}\)

So, the equation is \(\ x^{2}+y^{2}=98\). The radius of the circle is \(\ r=\sqrt{98}=7 \sqrt{2}\).

Finally, let's determine if the point \(\ (9,−11)\) is on the circle \(\ x^{2}+y^{2}=225\).

Substitute the point in for x and y and see if it equals 225.

\(\ \begin{aligned}
9^{2}+(-11)^{2} &=225 \\
81+121 & \stackrel{?}{=} 225 \\
202 & \neq 225
\end{aligned}\)

The point is not on the circle.

Examples

Example 1

Earlier, you were asked to determine if the point (14 ,8) lies on the circle that is centered at the origin and has a diameter of 32 units.

Solution

From this lesson, you know that the equation of a circle that is centered at the origin is \(\ x^{2}+y^{2}=r^{2}\), where \(\ r\) is the radius and \(\ (x,y)\) is any point on the circle.

With the point \(\ (14,8)\), \(\ x=14\) and \(\ y=8\). We are given the diameter, but we need the radius. Recall that the radius is half the diameter, so the radius is \(\ \frac{32}{2}=16\).

Plug these values into the equation of the circle. If they result in a true statement, the point lies on the circle.

\(\ \begin{array}{r}
x^{2}+y^{2}=r^{2} \\
14^{2}+8^{2} \stackrel{?}{=} 16^{2} \\
196+64 \stackrel{?}{=} 256 \\
260 \neq 256
\end{array}\)

Therefore the point does not lie on the circle.

Example 2

Graph and find the radius of \(\ x^{2}+y^{2}=4\).

Solution

\(\ r=\sqrt{4}=2\)

f-d_d00900a58ec8836d751020baa0f473994584a28d3837a33ec139e402+IMAGE_TINY+IMAGE_TINY.png

Example 3

Find the equation of the circle with a radius of \(\ 6 \sqrt{5}\).

Solution

Plug in \(\ 6 \sqrt{5}\) for \(\ r\) in \(\ x^{2}+y^{2}=r^{2}\)

\(\ \begin{array}{l}
x^{2}+y^{2}=(6 \sqrt{5})^{2} \\
x^{2}+y^{2}=6^{2} \cdot(\sqrt{5})^{2} \\
x^{2}+y^{2}=36 \cdot 5 \\
x^{2}+y^{2}=180
\end{array}\)

Example 4

Find the equation of the circle that passes through (5, 8).

Solution

Plug in (5, 8) for x and y, respectively.

\(\ \begin{aligned}
5^{2}+8^{2} &=r^{2} \\
25+64 &=r^{2} \\
89 &=r^{2}
\end{aligned}\)

The equation is \(\ x^{2}+y^{2}=89\)

Example 5

Determine if \(\ (−10, 7)\) is on the circle \(\ x^{2}+y^{2}=149\).

Solution

Plug in \(\ (−10, 7)\) to see if it is a valid equation.

\(\ \begin{aligned}
(-10)^{2}+7^{2} &=149 \\
100+49 &=149
\end{aligned}\)

Yes, the point is on the circle.

Review

Graph the following circles and find the radius.

\(\ x^{2}+y^{2}=9\)
\(\ x^{2}+y^{2}=64\)
\(\ x^{2}+y^{2}=8\)
\(\ x^{2}+y^{2}=50\)
\(\ 2 x^{2}+2 y^{2}=162\)
\(\ 5 x^{2}+5 y^{2}=150\)

Write the equation of the circle with the given radius and centered at the origin.

\(\ 14\)
\(\ 6\)
\(\ 9 \sqrt{2}\)

Write the equation of the circle that passes through the given point and is centered at the origin.

\(\ (7,−24)\)
\(\ (2,2)\)
\(\ (−9,−10)\)

Determine if the following points are on the circle, \(\ x^{2}+y^{2}=74\).

\(\ (−8,0)\)
\(\ (7,−5)\)
\(\ (6,−6)\)

Challenge In Geometry, you learned about tangent lines to a circle. Recall that the tangent line touches a circle at one point and is perpendicular to the radius at that point, called the point of tangency.

The equation of a circle is \(\ x^{2}+y^{2}=10\) with point of tangency \(\ (−3,1)\).
1. Find the slope of the radius from the center to \(\ (−3,1)\).
2. Find the perpendicular slope to (a). This is the slope of the tangent line.
3. Use the slope from (b) and the given point to find the equation of the tangent line.
Repeat the steps in #16 to find the equation of the tangent line to \(\ x^{2}+y^{2}=34\) with a point of tangency of \(\ (3,5)\).

Answers for Review Problems

To see the Review answers, open this PDF file and look for section 10.3.

Vocabulary

Term	Definition
center	The center of a circle is the point that defines the location of the circle. All points on the circle are equidistant from the center of the circle.
Circle	A circle is the set of all points at a specific distance from a given point in two dimensions.
Diameter	Diameter is the measure of the distance across the center of a circle. The diameter is equal to twice the measure of the radius.
Equation of a Circle	If the center of a circle is (0, 0), then the equation of the circle is of the form \(\ x^{2}+y^{2}=r^{2}\), where \(\ r\) is the radius.
Radius	The radius of a circle is the distance from the center of the circle to the edge of the circle.

Image Attributions

[Figure 1]
Credit: Tony Webster;Robert Pernett
Source: https://commons.wikimedia.org/wiki/File%3ALas_Vegas_High_Roller_(20216869960).jpg;https://flic.kr/p/nQD1fo