2.1: One-Sided Limit Types
- Page ID
- 1112
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A one sided limit is exactly what you might expect; the limit of a function as it approaches a specific x value from either the right side or the left side. One sided limits help to deal with the issue of a jump discontinuity and the two sides not matching.
Is the following piecewise function continuous?
\[f(x)=\left\{\begin{array}{cc}
-x-2 & x<1 \\
-3 & x=1 \\
x^{2}-4 & 1<x
\end{array}\right.\]
Evaluating One Sided Limits and Continuity
A one sided limit can be evaluated either from the left or from the right. Since left and right are not absolute directions, a more precise way of thinking about direction is “from the negative side” or “from the positive side”. The notation for these one sided limits is:
\[\lim _{x \rightarrow a^{-}} f(x)\]
and
\[\lim _{x \rightarrow a^{+}} f(x)\]
The negative in the superscript of a is not an exponent. Instead it indicates from the negative side. Likewise the positive superscript is not an exponent, it just means from the positive side. When evaluating one sided limits, it does not matter what the function is doing at the actual point or what the function is doing on the other side of the number. Your job is to determine what the height of the function should be using only evidence on one side.
Take the graph below. What are the one sided limits at -5, -1, 3 and 5?
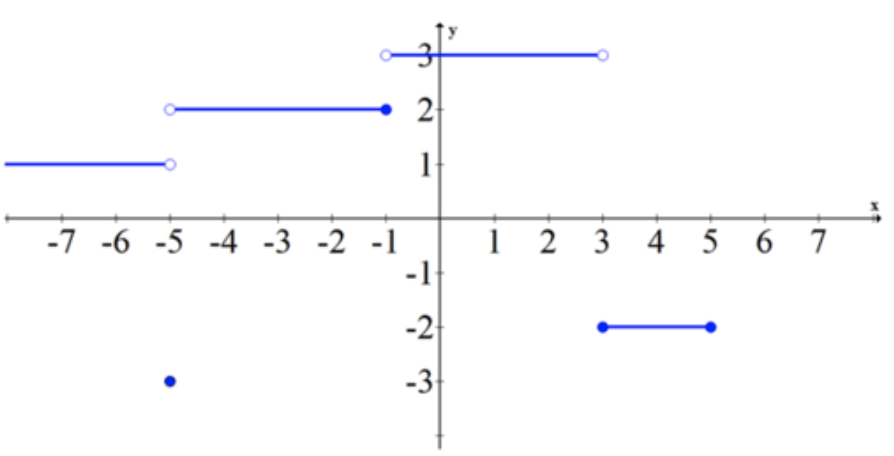
CK-12 Foundation - CCSA
Each point should have two limits, one from the left and one from the right.
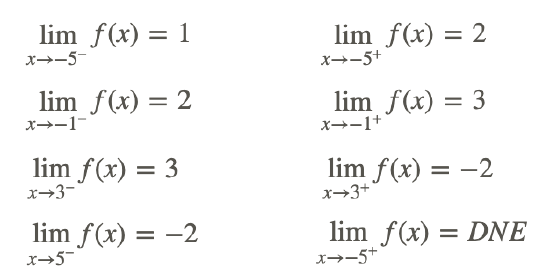
You have defined continuity in the past as the ability to draw a function completely without lifting your pencil off of the paper. You can now define a more rigorous definition of continuity.
Continuity at a point exists when the left and right sided limits match the function evaluated at that point. In other words, a function is continuous at a if:
\[\lim _{x \rightarrow a^{-}} f(x)=f(a)=\lim _{x \rightarrow a^{+}} f(x)\]
For an entire function to be continuous, the function must be continuous at every single point in an unbroken domain.
Examples
Example 1
Earlier, you were asked how to confirm the function
\[f(x)=\left\{\begin{array}{cc}
-x-2 & x<1 \\
-3 & x=1 \\
x^{2}-4 & 1<x
\end{array}\right.\]
is continuous. In order to confirm or deny that the function is continuous, graphical tools are not accurate enough. Sometimes jump discontinuities can be off by such a small amount that the pixels on the display of your calculator will not display a difference. Your calculator will certainly not display removable discontinuities.
You should note that on the graph, everything to the left of 1 is continuous because it is just a line. Next you should note that everything to the right of 1 is also continuous for the same reason. The only point to check is at x=1. To check continuity, explicitly use the definition and evaluate all three parts to see if they are equal.
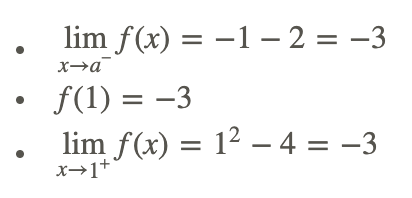
Therefore,
\[\lim _{x \rightarrow 1^{-}} f(x)=f(1)=\lim _{x \rightarrow 1^{+}} f(x)\]
and the function is continuous at x=1 and everywhere else.
Example 2
Evaluate the one sided limit at 4 from the negative direction numerically.
\[f(x)=\frac{x^{2}-7 x+12}{x-4}\]
Remember that evaluating numerically means that you should use a table. When creating the table, only use values that are smaller than 4.
| x | 3.9 | 3.99 | 3.999 |
| f(x) | 0.9 | 0.99 | 0.999 |
\[\lim _{x \rightarrow 4^{-}}\left(\frac{x^{2}-7 x+12}{x-4}\right)=1\]
Example 3
Evaluate the following limits.
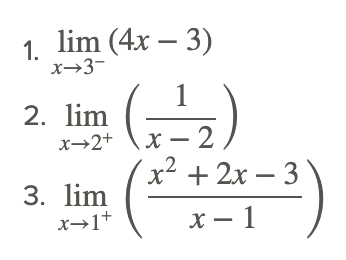
Most of the time one sided limits are the same as the corresponding two sided limit. The exceptions are when there are jump discontinuities, which normally only happen with piecewise functions, and infinite discontinuities, which normally only happen with rational functions.
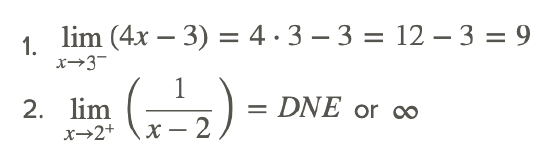
The reason why ∞ is preferable in this case is because the two sides of the limit disagree. One side goes to negative infinity and the other side goes to positive infinity (see the graph below). If you just indicate DNE then you are losing some perfectly good information about the nature of the function.
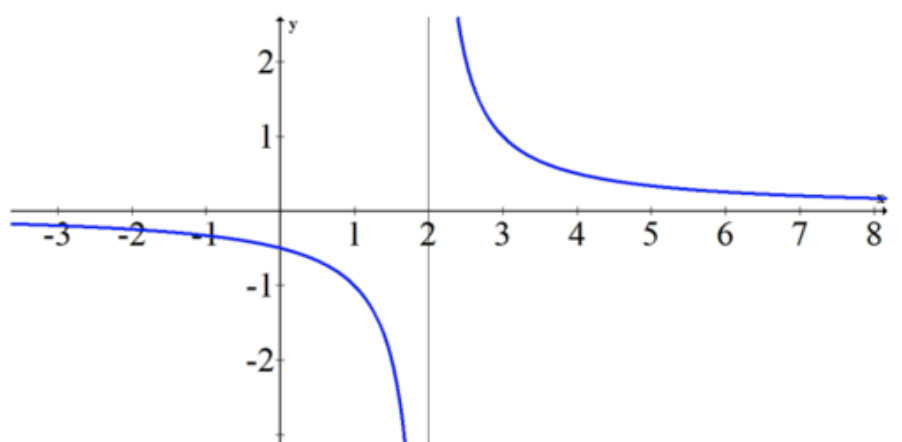
CK-12 Foundation - CCSA
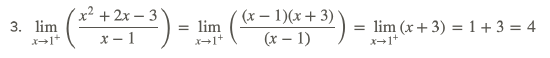
Example 4
Evaluate the following limits.
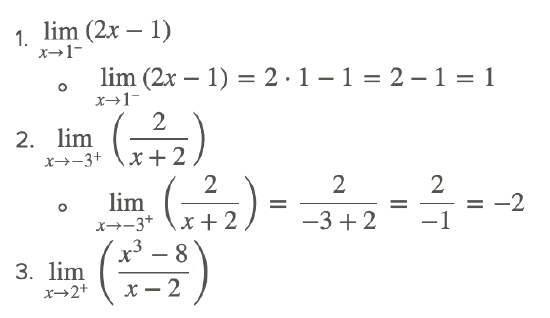
Example 5
Is the following function continuous?
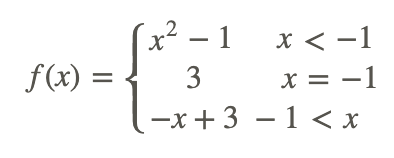
Use the definition of continuity.
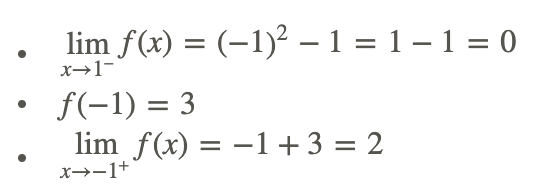
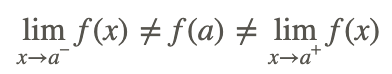
so this function is discontinuous at x=−1. It is continuous everywhere else.
Review
Evaluate the following limits.
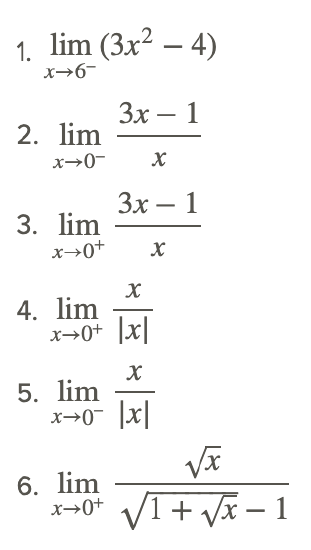
Consider
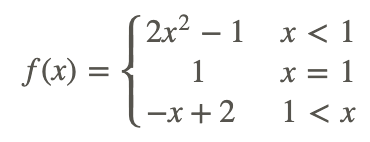
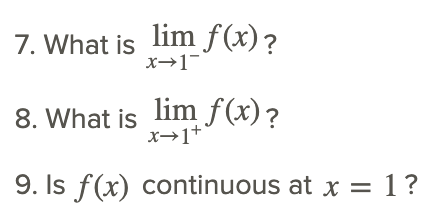
Consider
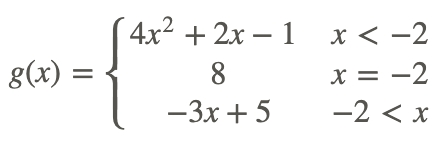
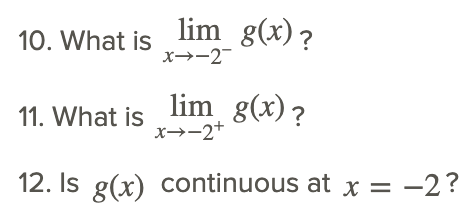
Consider h(x) shown in the graph below.
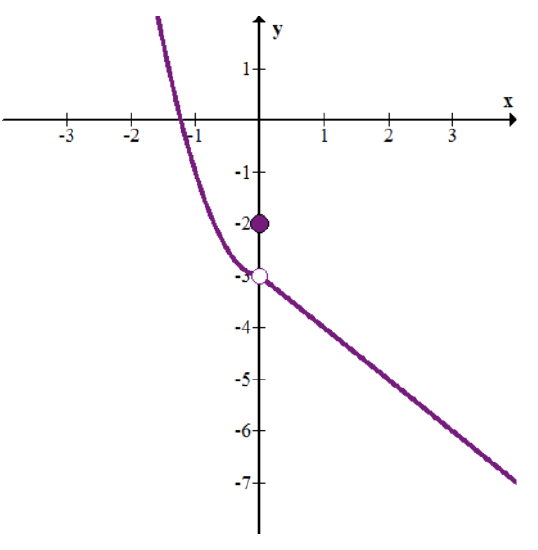
CK-12 Foundation - CCSA
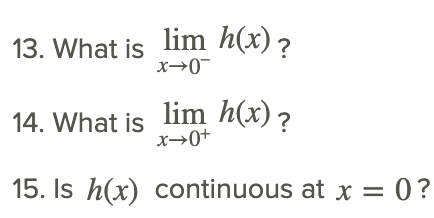
Vocabulary
| Term | Definition |
|---|---|
| continuity | Continuity for a point exists when the left and right sided limits match the function evaluated at that point. For a function to be continuous, the function must be continuous at every single point in an unbroken domain. |
| Continuous | Continuity for a point exists when the left and right sided limits match the function evaluated at that point. For a function to be continuous, the function must be continuous at every single point in an unbroken domain. |
| Jump discontinuities | Inverse functions are functions that 'undo' each other. Formally f(x) and g(x) are inverse functions if f(g(x))=g(f(x))=x. |
| limit | A limit is the value that the output of a function approaches as the input of the function approaches a given value. |
| Removable discontinuities | Removable discontinuities are also known as holes. They occur when factors can be algebraically canceled from rational functions. |
| Removable discontinuity | Removable discontinuities are also known as holes. They occur when factors can be algebraically canceled from rational functions. |
| two-sided limit | A two-sided limit is the value that a function approaches from both the left side and the right side. |
Additional Resources
PLIX: Play, Learn, Interact, eXplore - One-Sided Limits
Video: Determining Limits and One-Sided Limits Graphically
Practice: One-Sided Limit Types
Real World: Deep Freeze

