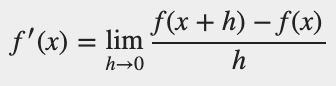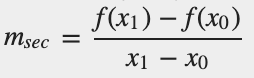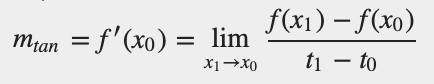4.1: Average and Instantaneous Rates of Change
- Page ID
- 1244
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)You may recall the story about Jim and his track-star girlfriend Becca from the lesson on understanding limits. The two of them were discussing how they might calculate her speed at the instant that Jim snapped a photo of her. The end result of the discussion was Becca pointing out that it is not technically possible to calculate the exact speed of something in a specific instant.
By now, we have explored the related concepts of limits and lines tangent to a curve, so we know it is possible to effectively calculate instantaneous speed. What process would be involved with actually calculating Becca's speed at the instant the photo was taken? What are the technical difficulties with identifying instantaneous speed?
Instantaneous Rates of Change
The function f′(x) that we defined in previous lessons is so important that it has its own name: the derivative.
The Derivative
|
|---|
Based on the discussion that we have had in previous section, the derivative f′ represents the slope of the tangent line at point x. Another way of interpreting it would be that the function y = f(x) has a derivative f′ whose value at x is the instantaneous rate of change of y with respect to point x.
One of the two primary concepts of calculus involves calculating the rate of change of one quantity with respect to another. For example, speed is defined as the rate of displacement with respect to time. If a person travels 120 miles in 4 hours, his speed is 120/4 = 30 mi/hr. This speed is called the average speed or the average rate of change of distance with respect to time. Of course the person who travels 120 miles at a rate of 30 mi/hr for 4 hr probably does not do so continuously. Though he probably slowed down or sped up during the 4-hour period, it does generally suffice to say that he traveled for 4 hours at an average rate of 30 miles per hour. However, if the driver strikes a tree, it would not be his average speed that determines his survival but his speed at the instant of the collision. Similarly, when a bullet strikes a target, it is not the average speed that is significant but its instantaneous speed at the moment it strikes. So here we have distinct kinds of speeds, average speed and instantaneous speed.
The average speed of an object is defined as the object's displacement ∆x divided by the time interval ∆t during which the displacement occurs:
| Average speed =v=△x/△t=x1−x0/t1−t0 |
|---|
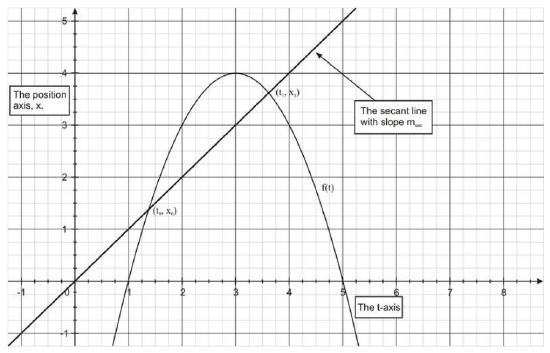
Notice that the points (t0, x0) and (t1, x1) lie on the position versus time curve, as the figure below shows.
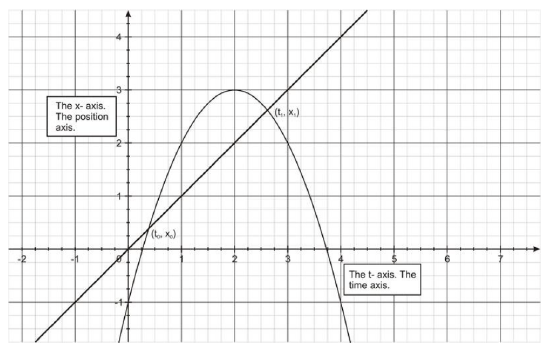
This expression is also the expression for the slope of a secant line connecting the two points. Thus we conclude that the average velocity of an object between time t0 and t1 is represented geometrically by the slope of the secant line connecting the two points (to, xo) and (t1, x1). If we choose t1 close to to, then the average velocity will closely approximate the instantaneous velocity at time to.
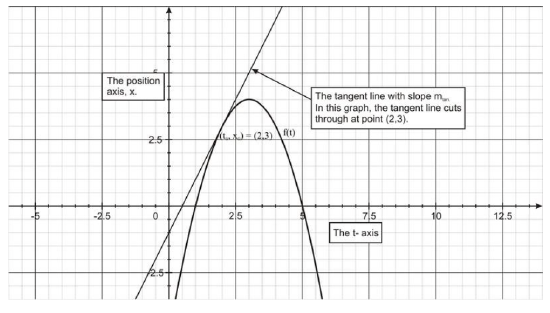
Geometrically, the average rate of change is represented by the slope of a secant line (figure a, below) and the instantaneous rate of change is represented by the slope of the tangent line (figure b, below).
|
Average Rate of Change (such as the average velocity) The average rate of change of y = f(x) over the time interval [x0, x1] is the slope msec of the secant line to the points (xo, f(x0)) and (x1, f(x0)) on the graph (figure a):
|
|---|
By now, we have explored the related concepts of limits and lines tangent to a curve, so we know it is possible to effectively calculate instantaneous speed. What process would be involved with actually calculating Becca's speed at the instant the photo was taken? What are the technical difficulties with identifying instantaneous speed?
Instantaneous Rates of Change
The function f′(x) that we defined in previous lessons is so important that it has its own name: the derivative.
The Derivative
|
|---|
Based on the discussion that we have had in previous section, the derivative f′ represents the slope of the tangent line at point x. Another way of interpreting it would be that the function y = f(x) has a derivative f′ whose value at x is the instantaneous rate of change of y with respect to point x.
One of the two primary concepts of calculus involves calculating the rate of change of one quantity with respect to another. For example, speed is defined as the rate of displacement with respect to time. If a person travels 120 miles in 4 hours, his speed is 120/4 = 30 mi/hr. This speed is called the average speed or the average rate of change of distance with respect to time. Of course the person who travels 120 miles at a rate of 30 mi/hr for 4 hr probably does not do so continuously. Though he probably slowed down or sped up during the 4-hour period, it does generally suffice to say that he traveled for 4 hours at an average rate of 30 miles per hour. However, if the driver strikes a tree, it would not be his average speed that determines his survival but his speed at the instant of the collision. Similarly, when a bullet strikes a target, it is not the average speed that is significant but its instantaneous speed at the moment it strikes. So here we have distinct kinds of speeds, average speed and instantaneous speed.
The average speed of an object is defined as the object's displacement ∆x divided by the time interval ∆t during which the displacement occurs:
| Average speed =v=△x△t=x1−x0t1−t0 |
|---|
Notice that the points (t0, x0) and (t1, x1) lie on the position versus time curve, as the figure below shows.
This expression is also the expression for the slope of a secant line connecting the two points. Thus we conclude that the average velocity of an object between time t0 and t1 is represented geometrically by the slope of the secant line connecting the two points (to, xo) and (t1, x1). If we choose t1 close to to, then the average velocity will closely approximate the instantaneous velocity at time to.
Geometrically, the average rate of change is represented by the slope of a secant line (figure a, below) and the instantaneous rate of change is represented by the slope of the tangent line (figure b, below).

| Instantaneous Rate of Change The instantaneous rate of change of y = f(x) at the point x0 is the slope msec of the tangent line to the point x0on the graph (figure b):
|
|---|
Examples
Example 1
Earlier, you were asked a question about the process of calculating Becca's speed in the race.
Speed is, by definition, a relation between a distance and the time required to cross that distance (recall d=rt from your science class). If the time required is zero, then you end up dividing by zero, which is an undefined function.
However, using calculus, you can identify what the end behavior of the function would be if you were to get infinitely close, and thereby effectively calculate the speed at a given instant. In fact, that is exactly what you did in the examples above.
Calculate: (a) The slope of the line tangent to y=x2+5 at the point on the curve x=4 and (b) the equation of that line.
In the previous concept "Tangents to a Curve" we showed how to calculate the derivative (the slope of the tangent) of a function of the form y=x2−c.
- The slope of the tangent to the curve y=x2+5 at x=4 is:
2(4)=8
Recall from algebra the "slope - intercept form" of a straight line: y=mx+b, where m is the slope of the line.
- Given m=8 from above, we have y=8x+b. All we need is to solve for b to have the full equation.
Substitute 4 (the point we are finding the slope of) in for x in the equation of the curve y=x2+5 to identify a corresponding y
y=(4)2+5
y=21
Substitute the values for x, y, and m that we now have into our y=mx+b form of the equation of the tangent line:
21=8(4)+b
−11=b
Use the calculated values for m and b to complete the equation:
y=8x−11
Example 3
Suppose that y=x2−3.
(a) Find the average rate of change of y with respect x over the interval [0, 2] and (b) find the instantaneous rate of change of y with respect x at the point x = −1.
- Applying the formula above for secant with f(x)=x2−3 and x0=0 and x1=2, yields
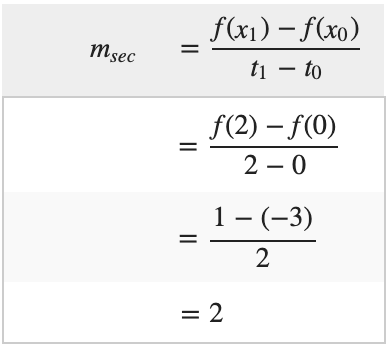
This means that the average rate of change of y is 2 units per unit increase in x over the interval [0,2].
b. Recall, for functions of the form y=x2+c that f′(x)=2x (f′(x) is "f prime of x," meaning "the slope (m) of the line tangent to x")

This means that the instantaneous rate of change is negative. That is, y is decreasing at the point x = -1. It is decreasing at a rate of 2 units per unit increase in x.
Example 4
Find the derivative of f(x)=x0.5 and the equation of the tangent line at x0 = 1.
Using the definition of the derivative,

Thus, the slope of the tangent line at x0 = 1 is
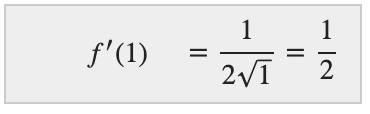
For x0 = 1, we can find y0 by simply substituting into f(x):
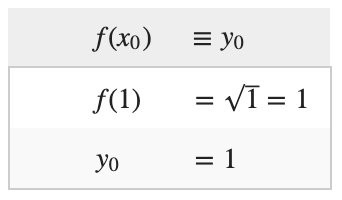
Thus the equation of the tangent line is
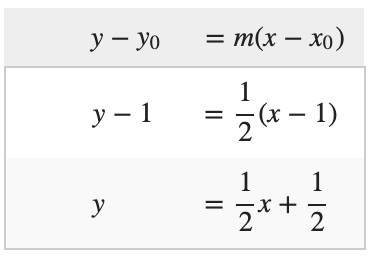
Example 5
Find the derivative of f(x)=x/x+1.
Using the derivative formula:

A rocket is propelled upwards and reaches a height of h(t) = 4.9t2 in t seconds.
- How high does it reach in 35 seconds?
The height of the rocket at 35 secs is 4.9(35)2=6002.5m
- What is the average velocity of the rocket during the first 35 seconds?
Vavg=6002.5m/35s=171.5m/s
- What is the instantaneous velocity of the rocket at the end of the 35 seconds?
To find the instantaneous speed, we need to find the derivative of h(t)=4.9t2
h′(t)=9.8t Using the instantaneous rate of change formula from above
9.8⋅35s=343m/sec
Example 7
A particle moves in the positive direction along a straight line so that after t nanoseconds, its traversed distance is given by χ(t)=9.9t3 nanometers.
- What is the average velocity of the particle during the first 2 nanoseconds?
The particle moves 9.9t3nm in t secs
∴ 9.9(23)=79.2nm/2s→39.6nm/1s
- What is the instantaneous velocity of the particle at t = 2 nanoseconds?
Using the formula for finding the derivative, we get χ′(t)=29.7t2
∴χ′(2)=118.8nm/s
∴ The instantaneous velocity at t=2 is 118.8 nm/sec
Review
Find the average rate of change:
- C=f(x) and f(x)=x2−4x+2. Find the average rate of change of (C) with respect to (x), when (x) is changed from x = 15, to x = 59.
- H=f(x) and f(x)=x2−5x+201 Find the average rate of change of (H), with respect to (x) when (x) is changed from x = 10 to x = 11.
- N=f(x) and f(x)=3x2−4x−1 Find the average rate of change of (N) with respect to (x) when (x) is changed is changed from x = 20 to x = 64.
- H=f(x) and f(x)=x2+10x+201 Find the average rate of change of (H) with respect to (x) when (x) is changed from x + 25 to x = 74.
- N=f(x) and f(x)=−5x2−3x−4 Find the average rate of change of (N) with respect to (x) when (x) is changed from x = 30 to x = 54.
Find the instantaneous rate of change:
- If C=f(x) and f(x)=−4x2+2x+5 Find the instantaneous rate of change of (C) with respect to (x) when x = 25.
- If N=f(x) and f(x)=3x2−x−5 Find the instantaneous rate of change of (N) with respect to x when x = 10.
- H=f(x) and f(x)=4x2+195 Find the instantaneous rate of change of (H) with respect to x when x = 10.
- N=f(x) and f(x)=−x2+x−3 Find the instantaneous rate of change of (N) with respect to x when x = 150.
- C=f(x) and f(x)=−3x2+4x−4 Find the instantaneous rate of change of (N) with respect to x when x = 20.
Use the definition of the derivative to find f(x) and then find the equation of the tangent line at x = x0.
- f(x) = 6x2; x0 = 3.
- f(x)=(x+2)0.5;x0=8
- f(x) = 3x3 - 2; x0 = -1
- f(x)=1x+2;x0=−1
- f(x) = ax2 - b , (where a and b are constants); x0 = b
- f(x) = x1/3; x0 = 1.
- Suppose that f has the property that f(x + y) = f(x) + f(y) + 3xy and
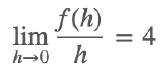 . Find f(0) and f'(x).
. Find f(0) and f'(x). - Find dy/dx
Solve the rate of change problems.
- A packing company in the south makes "Mama's Spaghetti Sauce." The cost of producing x jars is J = f(x) dollars. What does f'(100) = 9999 mean in this context?
- A cherry pie is taken from an oven when its temperature is 202°F and placed on a table in a room where the temperature is 75°F. The temperature of the pie over x minutes is given by T = f(x). What does f'(100) = 102 mean in this context?
- The number of virus, after (x) hours, in a controlled laboratory experiment is V = f(x). What are the units of f'(x)?
- The number of people in the US affected by the common cold in the month of November is defined by N = f(x) where x is the day of the month. What is the meaning of f'(x) in this context?
- The number of households in Florida affected by hurricane season in the month of July is defined by J = f(x) where x is the day of the month. f(x)=2x2+x+1 Find the average rate of change of J with respect to x when days is changed from x = 5 to x = 34.
- A cake is taken from an oven when its temperature is 196°F and placed on a cooling rack in a room where the temperature is 75°F. The temperature of the cake over (x) minutes is given by H = f(x). f(x)=4x2+15x+196 Find the instantaneous rate of change of H with respect to x when x = 15.
- A pan of meatloaf is taken from an oven when its temperature is 205°F and placed on a table in a room where the temperature is 75°F. The temperature of the meatloaf over x minutes is given by H = f(x). f(x)=2x2+5x+205. Find the average rate of change of H with respect to x when minutes is changed from x = 5 to x = 54.
Vocabulary
| Term | Definition |
|---|---|
| Average rate of change | The average rate of change of a function is the change in y coordinates of a function, divided by the change in x coordinates. |
| Average speed | The average speed of an object is the distance an object travels divided by the travel time |
| derivative | The derivative of a function is the slope of the line tangent to the function at a given point on the graph. Notations for derivative include f′(x), dydx, y′, dfdx and \frac{df(x)}{dx}. |
| instantaneous rate of change | The instantaneous rate of change of a curve at a given point is the slope of the line tangent to the curve at that point. |
| Instantaneous speed | The instantaneous speed of an object is the speed of the object at a specific point in time. |
| limit | A limit is the value that the output of a function approaches as the input of the function approaches a given value. |
| secant line | A secant line is a line that joins two points on a curve. |
| Slope | Slope is a measure of the steepness of a line. A line can have positive, negative, zero (horizontal), or undefined (vertical) slope. The slope of a line can be found by calculating “rise over run” or “the change in the y over the change in the x.” The symbol for slope is m |
| Tangent line | A tangent line is a line that "just touches" a curve at a single point and no others. |
Additional Resources
PLIX: Play, Learn, Interact, eXplore - Average and Instantaneous Rate of Change
Video: Rates-of-Changes
Practice: Average and Instantaneous Rates of Change
Real World: China Syndrome