Skip to main content
K12 LibreTexts

1.7: 1.7 Increasing and Decreasing

  1. Last updated
  2. Save as PDF
  • Page ID
    6998

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    It is important to be able to distinguish between when functions are increasing and when they are decreasing. In business this could mean the difference between making money and losing money. In physics it could mean the difference between speeding up and slowing down.

    How do you decide when a function is increasing or decreasing?

    Increasing and Decreasing Functions

    Increasing means places on the graph where the slope is positive.

    clipboard_e34f0d7535e58d3f9490dabe743d62ea9.png

    The formal definition of an increasing interval is: an open interval on the \(x\) axis of \((a, d)\) where every \(b, c \in(a, d)\) with \(b<c\) has \(f(b) \leq f(c)\)

    clipboard_ea21707d4aedfd262c91fd93b267ff817.png

    A interval is said to be strictly increasing if \(f(b)<f(c)\) is substituted into the
    definition.

    Decreasing means places on the graph where the slope is negative. The formal definition of decreasing and strictly decreasing are identical to the definition of increasing with the inequality sign reversed.

    clipboard_e5fffb9877b97f3629428aad519c8bde0.png

    A function is called monotonic if the function only goes in one direction and never switches between increasing and decreasing.

    Out of the basic functions, the monotonically increasing functions are:

    \(f(x)=x, f(x)=x^{3}, f(x)=\sqrt{x}, f(x)=e^{x}, f(x)=\ln x, f(x)=\frac{1}{1+e^{-x}}\)

    The only basic functions that are not monotonically increasing are:

    \(f(x)=x^{2}, f(x)=|x|, f(x)=\frac{1}{x}, f(x)=\sin x\)

    Identifying analytically where functions are increasing and decreasing often requires Calculus. For PreCalculus, it will be sufficient to be able to identify intervals graphically and through your knowledge of what the parent functions look like.

    Examples

    Example 1

    Earlier, you were asked how to determine if a function is increasing or decreasing. Increasing is where the function has a positive slope and decreasing is where the function has a negative slope. A common misconception is to look at the squaring function and see two curves that symmetrically increase away from zero. Instead, you should always read functions from left to right and draw slope lines and decide if they are positive or negative.

    Example 2

    Estimate where the following function is increasing and decreasing.


    clipboard_e1d91d5319c8f67f406f3ff101e3bf0d7.png

    Increasing: \(x \in(-\infty,-1.5) \cup(1.5, \infty)\).
    Decreasing: \(x \in(-1.5,1.5)\)

    Example 3

    Estimate where the following function is increasing and decreasing.

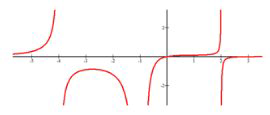
    clipboard_e68c6f0b5ae5b1bd7f0e0e187769da3dd.png

    Increasing \(x \in(-\infty,-4) \cup(-4,-2.7) \cup(-1,2) \cup(2, \infty)\).
    Decreasing \(x \in(-2.7,-1)\)

    Example 4

    Estimate the intervals where the function is increasing and decreasing.

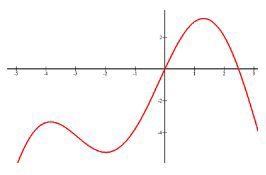
    clipboard_ecb3689630fdd2e28fddde1d96f732da4.png

    Increasing: \(x \in(-\infty,-4) \cup(-2,1.5)\)
    Decreasing: \(x \in(-4,-2) \cup(1.5, \infty)\)

    Notice that open intervals are used because at \(x=-4,-2,1.5\) the slope of the function is zero. This is here the slope transitions from being positive to negative. The reason why open parentheses are used is because the function is not actually increasing or decreasing at those specific points.

    Example 5

    A continuous function has a global maximum at the point (3, 2), a global minimum at (5, -12) and has no relative extrema or other places with a slope of zero. What are the increasing and decreasing intervals for this function?

    Increasing \(x \in(-\infty, 3) \cup(5, \infty)\).
    Decreasing \(x \in(3,5)\)

    Note: The \(y\) coordinates are not used in the intervals. A common mistake is to want to use the \(y\) coordinates.

    Review

    Use the graph below for 1-2.

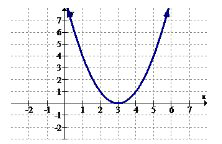
    clipboard_e0eb4499bc5048c86a3822536a0528b86.png

    1. Identify the intervals (if any) where the function is increasing.

    2. Identify the intervals (if any) where the function is decreasing.

    Use the graph below for 3-4.

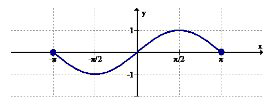
    clipboard_e0cb3d435f132bd7953a3fc9519cafabc.png

    3. Identify the intervals (if any) where the function is increasing.

    4. Identify the intervals (if any) where the function is decreasing.

    Use the graph below for 5-6.

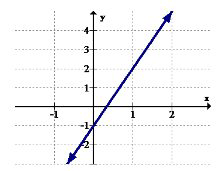
    clipboard_ea2e102851ca3669f113eb786413d59c1.png

    5. Identify the intervals (if any) where the function is increasing.

    6. Identify the intervals (if any) where the function is decreasing.

    Use the graph below for 7-8.

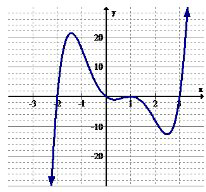
    clipboard_eb4550ac5252bda100ff36e384bb3aca9.png

    7. Identify the intervals (if any) where the function is increasing.

    8. Identify the intervals (if any) where the function is decreasing.

    Use the graph below for 9-10.

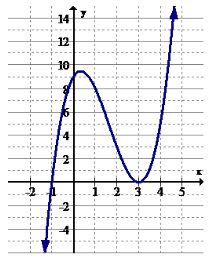
    clipboard_e38d8a6fff701f3894f15b9653e277e60.png

    9. Identify the intervals (if any) where the function is increasing.

    10. Identify the intervals (if any) where the function is decreasing.

    11. Give an example of a monotonically increasing function.

    12. Give an example of a monotonically decreasing function.

    13. A continuous function has a global maximum at the point (1, 4), a global minimum at (3, -6) and has no relative extrema or other places with a slope of zero. What are the increasing and decreasing intervals for this function?

    14. A continuous function has a global maximum at the point (1, 1) and has no other extrema or places with a slope of zero. What are the increasing and decreasing intervals for this function?

    15. A continuous function has a global minimum at the point (5, -15) and has no other extrema or places with a slope of zero. What are the increasing and decreasing intervals for this function?

    This page titled 1.7: 1.7 Increasing and Decreasing is shared under a CC BY-NC license and was authored, remixed, and/or curated by CK-12 Foundation via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.