2.9 Vertical Asymptotes

The basic rational function \(f(x)=\frac{1}{x}\) is a hyperbola with a vertical asymptote at \(x=0\). More complicated rational functions may have multiple vertical asymptotes. These asymptotes are very important characteristics of the function just like holes. Both holes and vertical asymptotes occur at \(x\) values that make the denominator of the function zero. A driving question is: what makes vertical asymptotes different from holes?

Finding Vertical Asymptotes

Vertical asymptotes occur when a factor of the denominator of a rational expression does not cancel with a factor from the numerator. When you have a factor that does not cancel, instead of making a hole at that \(x\) value, there exists a vertical asymptote. The vertical asymptote is represented by a dotted vertical line. Most calculators will not identify vertical asymptotes and some will incorrectly draw a steep line as part of a function where the asymptote actually exists.

Your job is to be able to identify vertical asymptotes from a function and describe each asymptote using the equation of a vertical line.

Take the following rational function:

\(f(x)=\frac{(2 x-3)(x+1)(x-2)}{(x+2)(x+1)}\)

To identify the holes and the equations of the vertical asymptotes, first decide what factors cancel out. The factor that cancels represents the removable discontinuity. There is a hole at (-1,15) . The vertical asymptote occurs at \(x=-2\) because the factor \(x+2\) does not cancel.

Watch the following video, focusing on the parts about vertical asymptotes.

Example 1

Earlier, you were asked how asymptotes are different than holes. Holes occur when factors from the numerator and the denominator cancel. When a factor in the denominator does not cancel, it produces a vertical asymptote. Both holes and vertical asymptotes restrict the domain of a rational function.

Example 2

Write a function that fits the following criteria:

• Vertical asymptotes at 0 and 3
• Zeroes at 2 and 5
• Hole at (4, 2)

Each criteria helps build the function. The vertical asymptotes imply that the denominator has two factors that do not cancel with the numerator:

\(\frac{1}{x \cdot(x-3)}\)

The zeroes at 2 and 5 imply the numerator has two factors that do not cancel.

\(\frac{(x-2)(x-5)}{x \cdot(x-3)}\)

The hole at (4,2) implies that there is a factor \(x-4\) that cancels on the numerator and the denominator.

\(\frac{(x-2)(x-5)(x-4)}{x \cdot(x-3)(x-4)}\)

The tricky part is that the height of the function must be 2 after the \(x-4\) factor has been canceled and the 4 is substituted in. Currently it is \(-\frac{1}{2}\)

\(\frac{(4-2)(4-5)}{4 \cdot(4-3)}=-\frac{1}{2}\)

In order to make the hole exist at a height of 2, you need to multiply the function by a scalar of -4.

\(f(x)=\frac{-4(x-2)(x-5)(x-4)}{x \cdot(x-3)(x-4)}\)

Example 3

Draw the vertical asymptotes for the following function.

\(f(x)=\frac{1}{(x-4)(x-2)(x+3)}\)

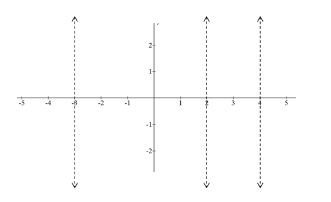
Note that you may not know the characteristics of what the function does inside these vertical lines. You will soon learn how to use sign tests as well as techniques you’ve already learned to fill in the four sections that this function is divided into.

Example 4

Identify the holes and equations of the vertical asymptotes of the following rational function.

\(f(x)=\frac{3(x-1)(x+2)(x-3)(x+4)}{5\left(x+\frac{1}{2}\right)(2+x)(3-x)(x-8)}\)

The vertical asymptotes occur at \(x=-\frac{1}{2}, x=8 .\) Holes occur when \(x\) is -2 and \(3 .\) To get the height of the holes at these points, remember to cancel what can be canceled and then substitute the values. A very common mistake is to forget to cancel \(\frac{x-3}{3-x}=-1\)

\(\begin{aligned} g(x) &=\frac{-3(x-1)(x+4)}{5\left(x+\frac{1}{2}\right)(x-8)} \\ g(-2) &=\frac{6}{25} \\ g(3) &=\frac{12}{25} \end{aligned}\)

The holes are at \(\left(-2, \frac{6}{25}\right),\left(3, \frac{12}{25}\right)\)

Example 5

Identify the domain of the following function and then identify the holes and vertical asymptotes.

\(f(x)=\frac{(3 x-4)(1-x)\left(x^{2}+4\right)}{(3 x-2)(x-1)}\)

The domain of the function written in interval notation is: \(\left(-\infty, \frac{2}{3}\right) \cup\left(\frac{2}{3}, 1\right) \cup(1, \infty) .\) Note that the domain is all real numbers except for where the denominator is zero.

There are two discontinuities: one is a hole and one is a vertical asymptote. The hole occurs at (1,5) The vertical asymptote occurs at \(x=\frac{2}{3}\)

Notice that holes are identified as points while vertical asymptotes are identified as lines of the form
\(x=a\) where \(a\) is some constant.

Review

1. Write a function that fits the following criteria:

• Vertical asymptotes at 1 and 4
• Zeroes at 3 and 5
• Hole at (6, 3)

2. Write a function that fits the following criteria:

• Vertical asymptotes at -2 and 2
• Zeroes at 1 and 5
• Hole at (3, -4)

3. Write a function that fits the following criteria:

• Vertical asymptotes at 0 and 3
• Zeroes at 1 and 2
• Hole at (8, 21)

4. Write a function that fits the following criteria:

• Vertical asymptotes at 2 and 6
• Zero at 5
• Hole at (4, 1)

5. Write a function that fits the following criteria:

• Vertical asymptote at 4
• Zeroes at 0 and 3
• Hole at (5, 10)

Give the equations of the vertical asymptotes for the following functions.

6. \(f(x)=\frac{(2-x)}{(x-2)(x-4)}\)

7. \(g(x)=\frac{-x}{(x+1)(x-3)}\)

8. \(h(x)=6-\frac{x+2}{(x+1)(x-5)}\)

9. \(j(x)=\frac{10}{x-3}-\frac{x}{(x+2)(x-3)}\)

10. \(k(x)=2-\frac{(4-x)}{(x+3)(x-4)}\)

Identify the holes and equations of the vertical asymptotes of the following rational functions.

11. \(f(x)=\frac{3(x-1)(x+1)(x-4)(x+4)}{4(x+4)(2+x)(4-x)(x+1)}\)

12. \(g(x)=\frac{x(x-3)(x-8)(x-3)(x+4)}{7(x+1)(1+x)(3-x)(x-8)}\)

State the domain of the following rational functions.

13. \(h(x)=\frac{x(x+1)(x-3)(x+4)}{x(3-x)(x-1)}\)

14. \(j(x)=\frac{x^{2}+3 x-4}{x^{2}-6 x-16}\)

15. \(k(x)=\frac{2 x-10}{x^{3}+4 x^{2}+3 x}\)