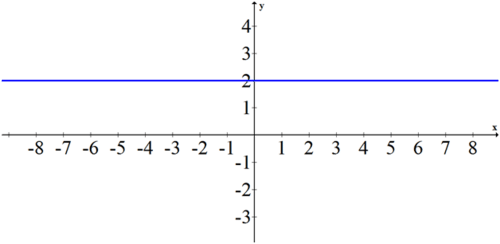10.1 Polar and Rectangular Coordinates

In the rectangular coordinate system, points are identified by their distances from the \(x\) and \(y\) axes. In the polar coordinate system, points are identified by their angle on the unit circle and their distance from the origin. You can use basic right triangle trigonometry to translate back and forth between the two representations of the same point. How are lines and other functions affected by this new coordinate system?

Polar and Rectangle Coordinates

Rectangular coordinates are the ordinary \((x, y)\) coordinates that you are used to.

Polar coordinates represent the same point, but describe the point by its distance from the origin \((r)\) and its angle on the unit circle \((\theta)\). To translate back and forth between polar and rectangular coordinates you should use the basic trig relationships:

\(\sin \theta=\frac{y}{r} \rightarrow r \cdot \sin \theta=y\)

\(\cos \theta=\frac{x}{r} \rightarrow r \cdot \cos \theta=x\)

\(\tan \theta=\frac{y}{x} \rightarrow \theta=\tan ^{-1} \frac{y}{x}\)

You can also express the relationship between \(x, y\) and \(r\) using the Pythagorean Theorem.

\(x^{2}+y^{2}=r^{2}\)

Note that coordinates in polar form are not unique. This is because there are an infinite number of coterminal angles that point towards any given \((x, y)\) coordinate.

For example, the point (3,4) can be written in polar coordinates in at least three different ways. To find \(\theta\), use the third equation from above and to find \(r\) use the pythagorean theorem.

\(\tan \theta=\frac{4}{3}\)

\(\theta=\tan ^{-1}\left(\frac{4}{3}\right) \approx 53.1^{\circ}\)

\(r^{2}=3^{2}+4^{2}\)

\(r=5\)

Three equivalent polar coordinates for the point (3,4) are:

\(\left(5,53.1^{\circ}\right), \quad\left(5,413.1^{\circ}\right), \quad\left(-5,233.1^{\circ}\right)\)

Notice how the third coordinate points in the opposite direction and has a seemingly negative radius. This means go in the opposite direction of the angle.

Once you can translate back and forth between points, use the same substitutions to change equations too. A polar equation is written with the radius as a function of the angle. This means an equation in polar form should be written in the form \(r=\) ___.

To write an equation in polar form, use the conversion equations to substitute. For example, to convert \(y=-x+1\) to polar form make substitutions for \(y\) and \(x\). Then, solve for \(r\).

\(\begin{aligned} r \cdot \sin \theta &=-r \cdot \cos \theta+1 \\ r \cdot \sin \theta+r \cdot \cos \theta &=1 \\ r(\sin \theta+\cos \theta) &=1 \\ r &=\frac{1}{\sin \theta+\cos \theta} \end{aligned}\)

Examples

Example 1

Earlier, you were asked how lines can be represented in the polar coordinate system. The general way to express a line \(y=m x+b\) in polar form is \(r=\frac{b}{\sin \theta-m \cdot \cos \theta}\).

Example 2

Express the following equation using rectangular coordinates: \(r=\frac{8}{1+2 \cos \theta}\).

Use the fact that \(r=\pm \sqrt{x^{2}+y^{2}}\) and \(r \cos \theta=x\).

\(\begin{aligned} r+2 r \cdot \cos \theta &=8 \\ \pm \sqrt{x^{2}+y^{2}}+2 x &=8 \\ \pm \sqrt{x^{2}+y^{2}} &=8-2 x \\ x^{2}+y^{2} &=64-32 x+4 x^{2}\\-3 x^{2}+32 x+y^{2}-64 &=0 \end{aligned}\)

This is the equation of a hyperbola.

Example 3

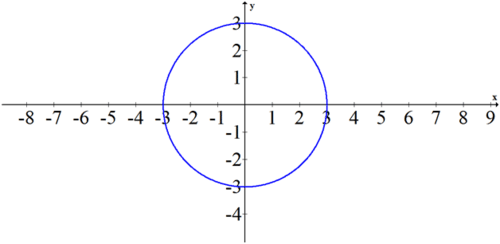
Sketch the following polar equation: \(r=3\).

Since theta is not in the equation, it can vary freely. This simple equation produces a perfect

circle of radius 3 centered at the origin.

You can show this equation is equivalent to \(x^{2}+y^{2}=9\)

Example 4

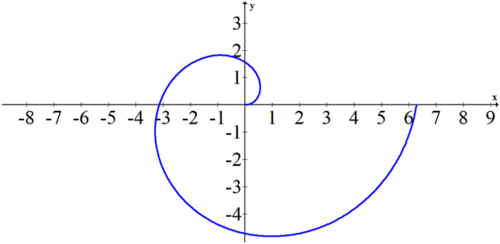
Sketch the following polar equation: \(r=\theta\) with \(\theta: 0 \leq \theta \leq 2 \pi\).

The equation \(r=\theta\) is an example of a polar equation that cannot be easily expressed in rectangular form. In order to sketch the graph, identify a few key points:

\((0,0),\left(\frac{\pi}{2}, \frac{\pi}{2}\right),(\pi, \pi),\left(\frac{3 \pi}{2}, \frac{3 \pi}{2}\right),(2 \pi, 2 \pi)\). You should see that the shape is very recognizable as a spiral.

Example 5

Translate the following polar expression into rectangular coordinates and then graph.

\(r=2 \cdot \sec \left(\theta-\frac{\pi}{2}\right)\)

Simplify the polar equation first before converting to rectangular coordinates.

\(\begin{aligned} r &=2 \cdot \sec \left(\theta-\frac{\pi}{2}\right) \\ r \cdot \cos \left(\theta-\frac{\pi}{2}\right) &=2 \\ r \cdot \cos \left(\frac{\pi}{2}-\theta\right) &=2 \\ r \cdot \sin \theta &=2 \\ y &=2 \end{aligned}\)

Review

Plot the following polar coordinates.

1. \(\left(3, \frac{5 \pi}{6}\right)\)

2. \(\left(2, \frac{\pi}{2}\right)\)

3. \(\left(4,-\frac{7 \pi}{6}\right)\)

4. \(\left(-2, \frac{5 \pi}{3}\right)\)

Give two alternate sets of coordinates for each point.

5. \(\left(2,60^{\circ}\right)\)

6. \(\left(5,330^{\circ}\right)\)

7. \(\left(2,210^{\circ}\right)\)

Graph each equation.

8. \(r=4\)

9. \(\theta=\frac{\pi}{4}\)

10. \(r=2 \theta\) with \(\theta: 0 \leq \theta \leq 2 \pi\).

Convert each point to rectangular form.

11. \(\left(4, \frac{2 \pi}{3}\right)\)

12. \(\left(3, \frac{\pi}{4}\right)\)

13. \(\left(5, \frac{\pi}{3}\right)\)

Convert each point to polar form using radians where \(0 \leq \theta<2 \pi\).

14. (1,3)

15. (1,-4)

16. (2,6)

Convert each equation to polar form.

17. \(x=3\)

18. \(2 x+4 y=2\