3.1: Collecting Data from Experiments
- Page ID
- 5705
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Experiment Techniques
A recent study published by the Royal Society of Britain1 concluded that there is a relationship between the nutritional habits of mothers around the time of conception and the gender of their children. The study found that women who ate more calories and had a higher intake of essential nutrients and vitamins were more likely to conceive sons. As we learned in the first chapter, this study provides useful evidence of an association between these two variables, but it is only an observational study. It is possible that there is another variable that is actually responsible for the gender differences observed. In order to be able to convincingly conclude that there is a cause and effect relationship between a mother’s diet and the gender of her child, we must perform a controlled statistical experiment. This lesson will cover the basic elements of designing a proper statistical experiment.
Lurking Variables
In an observational study such as the Royal Society’s connecting gender and a mother’s diet, it is possible that there is a third variable that was not observed that is causing a change in both the explanatory and response variables. A variable that is not included in a study but that may still have an effect on the other variables involved is called a lurking variable. Perhaps the existence of this variable is unknown or its effect is not suspected.
Confounding Variables
It's possible that in the study presented above, the mother’s exercise habits caused both her increased consumption of calories and her increased likelihood of having a male child.
A slightly different type of additional variable is called a confounding variable. Confounding variables are those that affect the response variable and are also related to the explanatory variable. The effect of a confounding variable on the response variable cannot be separated from the effect of the explanatory variable. They are both observed, but it cannot be distinguished which one is actually causing the change in the response variable.
Recognizing Lurking and Confounding Variables
The study described above also mentions that the habit of skipping breakfast could possibly depress glucose levels and lead to a decreased chance of sustaining a viable male embryo. In an observational study, it is impossible to determine if it is nutritional habits in general, or the act of skipping breakfast, that causes a change in gender birth rates. A well-designed statistical experiment has the potential to isolate the effects of these intertwined variables, but there is still no guarantee that we will ever be able to determine if one of these variables, or some other factor, causes a change in gender birth rates.
Observational studies and the public’s appetite for finding simplified cause-and-effect relationships between easily observable factors are especially prone to confounding. The phrase often used by statisticians is, “Correlation (association) does not imply causation.” For example, another recent study published by the Norwegian Institute of Public Health2 found that first-time mothers who had a Caesarian section were less likely to have a second child. While the trauma associated with the procedure may cause some women to be more reluctant to have a second child, there is no medical consequence of a Caesarian section that directly causes a woman to be less able to have a child. The 600,000 first-time births over a 30-year time span that were examined are so diverse and unique that there could be a number of underlying causes that might be contributing to this result.
Experiments: Treatments, Randomization, and Replication
There are three elements that are essential to any statistical experiment that can earn the title of a randomized clinical trial. The first is that a treatment must be imposed on the subjects of the experiment. In the example of the British study on gender, we would have to prescribe different diets to different women who were attempting to become pregnant, rather than simply observing or having them record the details of their diets during this time, as was done for the study. The next element is that the treatments imposed must be randomly assigned. Random assignment helps to eliminate other confounding variables. Just as randomization helps to create a representative sample in a survey, if we randomly assign treatments to the subjects, we can increase the likelihood that the treatment groups are equally representative of the population. The other essential element of an experiment is replication. The conditions of a well-designed experiment will be able to be replicated by other researchers so that the results can be independently confirmed.
To design an experiment similar to the British study, we would need to use valid sampling techniques to select a representative sample of women who were attempting to conceive. (This might be difficult to accomplish!) The women might then be randomly assigned to one of three groups in which their diets would be strictly controlled. The first group would be required to skip breakfast, the second group would be put on a high-calorie, nutrition-rich diet, and the third group would be put on a low-calorie, low-nutrition diet. This brings up some ethical concerns. An experiment that imposes a treatment which could cause direct harm to the subjects is morally objectionable, and should be avoided. Since skipping breakfast could actually harm the development of the child, it should not be part of an experiment.
It would be important to closely monitor the women for successful conception to be sure that once a viable embryo is established, the mother returns to a properly nutritious pre-natal diet. The gender of the child would eventually be determined, and the results between the three groups would be compared for differences.
Control
Let’s say that your statistics teacher read somewhere that classical music has a positive effect on learning. To impose a treatment in this scenario, she decides to have students listen to an MP3 player very softly playing Mozart string quartets while they sleep for a week prior to administering a unit test. To help minimize the possibility that some other unknown factor might influence student performance on the test, she randomly assigns the class into two groups of students. One group will listen to the music, and the other group will not. When the treatment of interest is actually withheld from one of the treatment groups, it is usually referred to as the control group. By randomly assigning subjects to these two groups, we can help improve the chances that each group is representative of the class as a whole.
Placebos and Blind Experiments
In medical studies, the treatment group usually receives some experimental medication or treatment that has the potential to offer a new cure or improvement for some medical condition. This would mean that the control group would not receive the treatment or medication. Many studies and experiments have shown that the expectations of participants can influence the outcomes. This is especially true in clinical medication studies in which participants who believe they are receiving a potentially promising new treatment tend to improve. To help minimize these expectations, researchers usually will not tell participants in a medical study if they are receiving a new treatment. In order to help isolate the effects of personal expectations, the control group is typically given a placebo. The placebo group would think they are receiving the new medication, but they would, in fact, be given medication with no active ingredient in it. Because neither group would know if they are receiving the treatment or the placebo, any change that might result from the expectation of treatment (this is called the placebo effect) should theoretically occur equally in both groups, provided they are randomly assigned. When the subjects in an experiment do not know which treatment they are receiving, it is called a blind experiment.
If you wanted to do an experiment to see if people preferred a brand-name bottled water to a generic brand, you would most likely need to conceal the identity of the type of water. A participant might expect the brand-name water to taste better than a generic brand, which would alter the results. Also, sometimes the expectations or prejudices of the researchers conducting the study could affect their ability to objectively report the results, or could cause them to unknowingly give clues to the subjects that would affect the results. To avoid this problem, it is possible to design the experiment so that the researcher also does not know which individuals have been given the treatment or placebo. This is called a double-blind experiment. Because drug trials are often conducted or funded by companies that have a financial interest in the success of the drug, in an effort to avoid any appearance of influencing the results, double-blind experiments are considered the gold standard of medical research.
Blocking
Blocking in an experiment serves a purpose similar to that of stratification in a survey. For example, if we believe men and women might have different opinions about an issue, we must be sure those opinions are properly represented in the sample. The terminology comes from agriculture. In testing different yields for different varieties of crops, researchers would need to plant crops in large fields, or blocks, that could contain variations in conditions, such as soil quality, sunlight exposure, and drainage. It is even possible that a crop’s position within a block could affect its yield. Similarly, if there is a sub-group in the population that might respond differently to an imposed treatment, our results could be confounded. Let’s say we want to study the effects of listening to classical music on student success in statistics class. It is possible that boys and girls respond differently to the treatment, so if we were to design an experiment to investigate the effect of listening to classical music, we want to be sure that boys and girls were assigned equally to the treatment (listening to classical music) and the control group (not listening to classical music). This procedure would be referred to as blocking on gender. In this manner, any differences that may occur in boys and girls would occur equally under both conditions, and we would be more likely to be able to conclude that differences in student performance were due to the imposed treatment. In blocking, you should attempt to create blocks that are homogenous (the same) for the trait on which you are blocking.
Implementing Blocking
In your garden, you would like to know which of two varieties of tomato plants will have the best yield. There is room in your garden to plant four plants, two of each variety. Because the sun is coming predominately from one direction, it is possible that plants closer to the sun would perform better and shade the other plants. Therefore, it would be a good idea to block on sun exposure by creating two blocks, one sunny and one not.
You would randomly assign one plant from each variety to each block. Then, within each block, you would randomly assign each variety to one of the two positions.
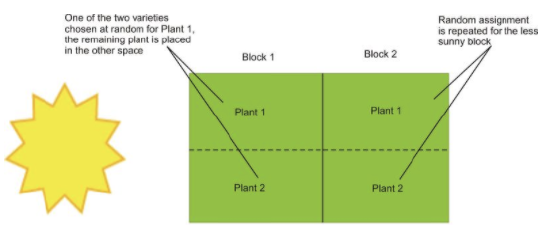
This type of design is called randomized block design.
Matched Pairs Design
A matched pairs design is a type of randomized block design in which there are two treatments to apply.
Suppose you were interested in the effectiveness of two different types of running shoes. You might search for volunteers among regular runners using the database of registered participants in a local distance run. After personal interviews, a sample of 50 runners who run a similar distance and pace (average speed) on roadways on a regular basis could be chosen. Suppose that because you feel that the weight of the runners will directly affect the life of the shoe, you decided to block on weight. In a matched pairs design, you could list the weights of all 50 runners in order and then create 25 matched pairs by grouping the weights two at a time. One runner would be randomly assigned shoe A, and the other would be given shoe B. After a sufficient length of time, the amount of wear on the shoes could be compared.
In the previous example, there may be some potential confounding influences. Factors such as running style, foot shape, height, or gender may also cause shoes to wear out too quickly or more slowly. It would be more effective to compare the wear of each shoe on each runner. This is a special type of matched pairs design in which each experimental unit becomes its own matched pair. Because the matched pair is in fact two different observations of the same subject, it is called a repeated measures design. Each runner would use shoe A and shoe B for equal periods of time, and then the wear of the shoes for each individual would be compared. Randomization could still be important, though. Let’s say that we have each runner use each shoe type for a period of 3 months. It is possible that the weather during those three months could influence the amount of wear on the shoe. To minimize this, we could randomly assign half the subjects shoe A, with the other half receiving shoe B, and then switch after the first 3 months.
Examples
For each of the following situations, explain whether an experiment could be used.
Example 1
To study the relationships between high blood pressure and amount of time spent doing physical exercise.
This can be an experiment with the researcher controlling the variable time spent doing exercise.
Example 2
To determine if taking a review course improves test scores on college entrance exams.
An experiment can be used here. Students would be randomly assigned to group that doesn’t take a review course and others would be assigned to group that does take a review course. Compare the scores of the two groups. You would have to control for many variables that might affect the result.
Example 3
To study the relationship between age and political party affiliation.
To study this relationship you would use an observational study. You are not imposing a treatment.
Example 4
To study the relationship between age and opinion on the death penalty.
This would be an observational study since you are not imposing a treatment.
Review
- As part of an effort to study the effect of intelligence on survival mechanisms, scientists recently compared a group of fruit flies intentionally bred for intelligence to the same species of ordinary flies. When released together in an environment with high competition for food, the percentage of ordinary flies that survived was significantly higher than the percentage of intelligent flies that survived.
- Identify the population of interest and the treatments.
- Based on the information given in this problem, is this an observational study or an experiment?
- Based on the information given in this problem, can you conclude definitively that intelligence decreases survival among animals?
- In order to find out which brand of cola students in your school prefer, you set up an experiment where each person will taste two brands of cola, and you will record their preference.
- How would you characterize the design of this study?
- If you poured each student a small cup from the original bottles, what threat might that pose to your results? Explain what you would do to avoid this problem, and identify the statistical term for your solution.
- Let’s say that one of the two colas leaves a bitter after-taste. What threat might this pose to your results? Explain how you could use randomness to solve this problem.
- You would like to know if the color of the ink used for a difficult math test affects the stress level of the test taker. The response variable you will use to measure stress is pulse rate. Half the students will be given a test with black ink, and the other half will be given the same test with red ink. Students will be told that this test will have a major impact on their grades in the class. At a point during the test, you will ask the students to stop for a moment and measure their pulse rates. In preparation for this experiment, you measure the at-rest pulse rates of all the students in your class.
- Here are those pulse rates in beats per minute:
-
-
Student Number At Rest Pulse Rate 1 46 2 72 3 64 4 66 5 82 6 44 7 56 8 76 9 60 10 62 11 54 12 76
-
-
- a. Using a matched pairs design, identify the students (by number) that you would place in each pair.
-
- b. Seed the random number generator on your calculator using 623.

- Use your calculator to randomly assign each student to a treatment. Explain how you made your assignments.
-
- c. Identify any potential lurking variables in this experiment.
-
- d. Explain how you could redesign this experiment as a repeated measures design?
- A recent British study was attempting to show that a high-fat diet was effective in treating epilepsy in children. According to the New York Times, this involved, “...145 children ages 2 to 16 who had never tried the diet, who were having at least seven seizures a week and who had failed to respond to at least two anticonvulsant drugs."
a. What is the population in this example?
b. One group began the diet immediately; another group waited three months to start it. In the first group, 38% of the children experienced a 50% reduction in seizure rates, and in the second group, only 6 percent saw a similar reduction prior to beginning the diet. What information would you need to be able to conclude that this was a valid experiment?
c. Identify the treatment and control groups in this experiment.
d. What conclusion could you make from the reported results of this experiment? - Researchers want to know how chemically fertilized and treated grass compares to grass grown using only organic fertilizer. Also, they believe that the height at which the grass is cut will affect the growth of the lawn. To test this, grass will be cut at three different heights: 1 inch, 2 inches, and 4 inches. A lawn area of existing healthy grass will be divided up into plots for the experiment. Assume that the soil, sun, and drainage for the test areas are uniform. Explain how you would implement a randomized block design to test the different effects of fertilizer and grass height. Draw a diagram that shows the plots and the assigned treatments.
- What are some other ways that researchers design more complicated experiments?
- When one treatment seems to result in a notable difference, how do we know if that difference is statistically significant?
- How can the selection of samples for an experiment affect the validity of the conclusions?
- Design a matched pairs experiment to determine whether students prefer the taste of Pepsi or Coke when the test is blind.
- Twenty overweight males agree to participate in a study of the effectiveness of 5 different diets. The researcher calculates how many pounds overweight each subject is by looking at the difference of the subject’s weight to his ideal weight. The researcher uses a randomized block design.
a. How many experimental units are there?
b. How many factors are there?
c. How many treatments are there?
d. How many blocks will the researcher set up? Explain.
e. How many subjects will there be in each block? Explain.
f. Describe how the subjects within each block will be assigned to a treatment. - A group of 300 first grade students is available to compare the effectiveness of two different methods for teaching arithmetic.
a. Outline the design of an experiment to make this comparison. What will your response variable be? - You want to compare three treatments for preventing the common cold: a vaccine, 1 gram of vitamin C taken daily and a placebo. You have 300 subjects available to you. Describe how you would use these subjects in an experiment to compare these treatments.
- Describe the difference between an observational study and an experiment. What advantages do experiments have over observational studies?
- A teacher wants to study the effectiveness of computer software that teaches arithmetic with the standard arithmetic curriculum for first grade students. She determines the level of each student in the class and divides them into two groups: one will have instruction on the computer; the other will have the standard curriculum. At the end of the year the two groups are retested and compared for increase in facility with arithmetic.
a. Is this an experiment?
b. What are the explanatory and response variables?
c. If teachers are asked to volunteer to use the computer software, are there any confounding variables? Explain. - Experiments can help determine cause and effect. Discuss some difficulties that can occur in the use of experiments.
- Find an example of an observational study in the news. Specify the explanatory and response variables and explain whether confounding variables were likely to be a major problem in interpreting the results.
- Find an example of a randomized experiment in the news.
a. What are the explanatory and response variables? Was a relationship between them found?
b. What treatments were assigned?
c. Was a control group used or a placebo?
d. Was the study a matched-pair design, a block design or neither?
e. Was the study single blind, double blind or neither? - A study reported in the Journal of Pediatrics, DOI 10.1016/j.peds.2010.07.026, published by Elsevier, looked at the relationship between dog ownership and eczema in children. Data was gathered from 636 children who were enrolled in a allergy study which was examining the effects of environmental particulates on childhood allergy development. The children enrolled were considered to be at high risk for developing allergies because both of their parents had allergies. The children were tested for 17 different allergies on a yearly basis from ages 1 to 4 and their parents completed surveys. The study concluded that if children who tested positive for dog allergies had a dog before age 1 year, they were less likely to develop eczema by age 4 years. Do you think this is based on an observational study or an experiment? Explain.
- A study considering the association of suicide attempts with acne and treatment with the drug isotretinoin was reported in the British Medical Journal, 2010:341:c5812. The objective of the study was to assess the risk of attempted suicide before, during and after treatment of severe acne with this drug. Over 5,000 patients, aged 15 to 49 years were prescribed the drug and observed before, during and after the treatment. The conclusion of the study was that there was an increased risk of attempted suicide up to six months after ending treatment with the drug.
a. Was this an observational study or an experiment? Explain.
b. Give an example of a possible confounding variable in this study. - Choose an issue of public policy that you feel could be clarified by an experiment. Discuss the statistical design of your experiment. What are the treatments? What are the response variables? Do you recommend blocking?
Vocabulary
| Term | Definition |
|---|---|
| blind experiment | If the participants are not aware of the treatment they are receiving, it is called a blind experiment. |
| blocking | Blocking is a technique used to control the potential confounding of variables. |
| cause-and-effect | A cause-effect relationship is a relationship in which one event (the cause) makes another event happen (the effect). |
| control group | A control group is a set of members deliberately kept as separate as possible from a particular study so as to provide an example of how the members should appear if unchanged. |
| confounding variables | Confounding variables are those that affect the response variable and are also related to the explanatory variable. |
| double-blind experiment | When neither the participant nor the researcher is aware of which subjects are receiving the treatment and which subjects are receiving a placebo, it is called a double-blind experiment. |
| lurking variables | If there is an additional explanatory variable affecting the response variable that was not considered in an experiment, it is called a lurking variable. |
| MAT.PRB.720, MAT.STA.224, MAT.STA.212.1 , MAT.STA.212.L.2 | All statistical experiments have three things in common: (1) the experiment can have more than one possible outcome, (2) each possible outcome can be specified in advance, and (3) the outcome of the experiment depends on chance. |
| matched pairs design | A matched pairs design is a type of randomized block design in which there are two treatments to apply. |
| observational study | An observational study draws inferences about the possible effect of a treatment on subjects, where the assignment of subjects into a treated group versus a control group is outside the control of the investigator. |
| placebo effect | The placebo effect occurs, for example, in medical experiments where the psychological effect of believing you are receiving a potentially effective treatment can lead to different results. |
| randomization | For randomization you have a simple random sample of size n (commonly referred to as an SRS) taken from a population, all possible samples of size n in the population have an equal probability of being selected for the sample. |
| repeated measures design | Repeated measures design uses the same subjects with every branch of research, including the control. |
| replication | Replication is an element of a statistical experiment where the conditions of an experiment are replicated by other researchers so that the results can be independently confirmed. |
| treatment | A treatment is an element of a statistical experiment that is imposed on the subjects of the experiment. |
Additional Resources
Video: Matched Pairs Experiment
Practice: Collecting Data from Experiments

