3.8: Stratified Random Sampling
- Page ID
- 5712
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Suppose you wanted to find out if age influences the choice of classes for students at a particular university. You might divide the students up by age ranges such as: Under 18, 18 – 21, 21 – 25, 25 – 35, and 35 and over. How could you make sure a random sample of college students would have members of each age range?
Look to the end of the lesson for the answer.
Stratified Random Sampling
Stratified random sampling is an excellent method of choosing members of a sample when there are clearly defined subgroups in the population you are studying. Each subgroup, called a stratum (strata if plural), should have a clearly defined characteristic that separates the members from the rest of the population.
To implement stratified sampling, first find the total number of members in the population, and then the number of members of each stratum. For each stratum, divide the number of members by the total number in the entire population to get the percentage of the population represented by that stratum. Finally, take the percentage and multiply by the number of units you want in your final sample group to see how many you need from each stratum. Always round any decimals upto whole units assuming you cannot take half of a sample.
As a formula, this process looks like:
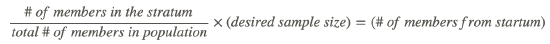
Conducting a Stratified Sample
How many Blue Heelers would you need for a stratified sampling of 50 dogs from a population consisting of:
- 247 Collies
- 138 Pit Bulls
- 96 English Mastiffs
- 172 Blue Heelers
- 222 Welsh Corgis
First identify the total number of dogs in the population:
247+138+96+172+222=875 dogs
Then divide the number of Blue Heelers by the population count:
172/875=.197 or 19.7%
Finally, multiply this number by the desired sample size:
.197×50=9.85→ rounds to 10 Blue Heelers
Determining Number of Participants Needed
How many members would you need from each age stratum to obtain a stratified sample of 350 from the following population?
| Age | Count |
| 15yrs to 18yrs | 297 |
| 18yrs to 21yrs | 349 |
| 21yrs to 27yrs | 323 |
| 27yrs to 35yrs | 240 |
| 35yrs to 42yrs | 191 |
First find the total population count:
297+349+323+240+191=1500
Then divide the count of each stratum by the total to get the percentage:
| Age | Count | % |
| 15yrs to | 297 | 297/1400=21.2% |
| 18yrs to | 349 | 349/1400=24.9% |
| 21yrs to | 323 | 323/1400=23.0% |
| 27yrs to | 240 | 240/1400=17.1% |
| 35yrs to | 191 | 191/1400=13.6% |
Finally, multiply the percentage of each stratum by the desired sample size:
- 15 – 18yrs: 21.2% of 350 = 74.2 → round to 74
- 18 – 21yrs: 24.9% of 350 = 87.15 → round to 87
- 21 – 27yrs: 23% of 350 = 80.5 → round to 80
- 27 – 35yrs: 17.1% of 350 = 59.85 → round to 60
- 35 – 42yrs: 13.6% of 350 = 47.6 → round to 48
Determining Appropriate Number of Samples Needed
Would it be appropriate to use 42 samples of green and 78 samples of blue marbles for a stratified sample of 120 marbles from a population of 960 green and 1500 blue marbles?
Just compare the ratios of each color:
- Green sample ratio: 42/120 = .35
- Green population ratio: 960/2460 = .39
- Blue sample ratio: 78/120 = .65
- Blue population ratio: 1500/2460 = .61
We can see by looking at the ratios that the actual population that they don’t quite match. There should be 47 green and 73 blue in the sample. This may not seem like enough of a difference to pose a problem, but notice that the 5 too few green marbles is more than 10% of the sample, and the 5 too many blues is nearly 10% of the blue sample. That is enough to possibly skew the results.
Earlier Problem Revisited
Suppose you wanted to find out if age influences the choice of classes for students at a particular university. You might divide the students up by age ranges such as: Under 18, 18 – 21, 21 – 25, 25 – 35, and 35 and over. How could you make sure a random sample of college students would have members of each age range?
By now, I’m sure you can see that a stratified sample would be perfect for this situation.
Examples
Example 1
Ivana wants to create a sample of the students in her school to see if it would be a good idea to put up posters of country music bands in each grade’s locker hall. Is this a good situation to use a stratified sample?
Yes, absolutely. Ivana will want to get a sample of the students in the school that is stratified by grade level to make sure each grade will appreciate the posters, since she plans to put them up in each hall.
Example 2
If Laurana wants to create a stratified sample of the distance an arrow can be shot from each of several different types of bows in the population of bows from her tribe, will she need to get a complete count of every single bow owned by every tribe member?
Inconveniently, yes. If she does not get a full count, she will not be able to come up with an accurate ratio to 'aim for' in her bow sample. Since she wants to use her sample to make prediction s about the entire population, she needs to be sure she has a true random sample. She needs to be certain that each bow has an equal chance of ending up in the same sample.
Example 3
If Tanis wants to investigate the waterproofing of Kitiara’s 200 pairs of boots, should he first try to separate them into different groups by style or maker?
It would be a good idea, yes. Different makers or styles are liable to be more similar to each other than to the entire population.
Review
For questions 1-5, assume you intend to create a stratified sample of 250 from a population of 920 trucks, 1540 subcompact cars, 1320 sedans, 450 motorcycles, 110 R.V.’s, 550 luxury cars, and 780 sports cars.
1. What percentage of the population is represented by sedans?
2. How many motorcycles should you have in your sample?
3. How many subcompacts should you have in your sample?
4. Is 10 R.V.’s a good number for your sample?
5. Should you have more than 15% of your sample represented by trucks?
For questions 6-10, assume your stratified sample consists of 29 cats, 62 small dogs, 48 large dogs, 19 birds, 37 pot-bellied pigs, and 55 horses. Assume the total population of pets is 6474.
6. How many horses are there in the entire population?
7. What percentage of the population is represented by dogs?
8. Are there more than 1000 pot-bellied pigs in the population?
9. What would the total population be if there were no horses?
10. What percent of the sample is made up of cats?
For questions 11-15, decide whether a stratified sample is warranted and why.
11. The estimated mileage of U.S. automobiles compared to vehicle weight.
12. The average height of college basketball players.
13. The G.P.A. of students in various sports.
14. The number students in your school with access to the internet.
15. Homework grades of sports participants.
Vocabulary
| Term | Definition |
|---|---|
| stratified sampling | Stratified Sampling involves choosing a proportional number of representatives from each of a number of subgroups of the initial population. |
| stratum | A stratum is a single category or sub-population out of a larger population. |
| subgroups | Subgroups are another name for stratum. |
Additional Resources
PLIX: Play, Learn, Interact, eXplore - An Extracurricular Study
Practice: Stratified Random Sampling
Real World: A Good Showing

