3.2.8: Trigonometric Equations Using Factoring

Factoring and the Quadratic Formula.

Solving trig equations is an important process in mathematics. Quite often you'll see powers of trigonometric functions and be asked to solve for the values of the variable which make the equation true. For example, suppose you were given the trig equation

\(2\sin x \cos x=\cos x\)

Trigonometric Equations Using Factoring

You have no doubt had experience with factoring. You have probably factored equations when looking for the possible values of some variable, such as "\(x\)". It might interest you to find out that you can use the same factoring method for more than just a variable that is a number. You can factor trigonometric equations to find the possible values the function can take to satisfy an equation.

Algebraic skills like factoring and substitution that are used to solve various equations are very useful when solving trigonometric equations. As with algebraic expressions, one must be careful to avoid dividing by zero during these maneuvers.

Solving for Unknown Values

1. Solve \(2\sin^2 x−3\sin x+1=0\) for \(0<x \leq 2\pi\).

\(\begin{aligned} \qquad \qquad \quad x^2 \sin^2 x−3\sin x+1&=0 \qquad \text{Factor this like a quadratic equation} \\ \qquad \qquad \quad (2\sin x−1)(\sin x−1)&=0 \end{aligned} \\ \begin{aligned} & \downarrow & \searrow& \\ 2\sin x−1&=0 &\text{or} \quad \sin x−1&=0 \\ 2\sin x&=1 & \sin x&=1 \\ \sin x&=\dfrac{1}{2} & x&=\dfrac{\pi}{2} \\ x=\dfrac{\pi}{6} \text{ and } x&=\dfrac{5\pi}{6} & & \end{aligned} \)

2. Solve \(2 \tan x \sin x+2\sin x=\tan x+1\) for all values of \(x\).

Figure \(\PageIndex{1}\)

Pull out \(\sin x\)

There is a common factor of \((\tan x+1)\)

Think of the \(−(\tan x+1)\) as \((−1)(\tan x+1)\), which is why there is a \(−1\) behind the \(2 \sin x\).

3. Solve \(2\sin^2 x+3\sin x−2=0\) for all \(x\), \([0,\pi ]\).

\(\begin{aligned}
\qquad \quad 2 \sin ^{2} x+3 \sin x-2&=0 \rightarrow \text { Factor like a quadratic }\\
\qquad \quad (2 \sin x-1)(\sin x+2)&=0 \end{aligned} \\ \begin{aligned} \swarrow&& \qquad \searrow &\\
2 \sin x-1 &=0 & \sin x+2&=0 \\
\sin x&=\dfrac{1}{2} & \sin x&=-2 \end{aligned}\)
\(x=\dfrac{\pi}{6} \text { and } x=\dfrac{5 \pi}{6} \text { There is no solution because the range of } \sin x \text { is }[-1,1] \text { . }\)

Some trigonometric equations have no solutions. This means that there is no replacement for the variable that will result in a true expression.

Example \(\PageIndex{1}\)

Earlier, you were asked to solve this:

\(2 \sin x \cos x=\cos x\)

Solution

Subtract \(\cos x\) from both sides and factor it out of the equation:

\(\begin{aligned} 2\sin x \cos x−\cos x&=0 \\ \cos x(2\sin x−1)&=0 \end{aligned}\)

Now set each factor equal to zero and solve. The first is \(\cos x\):

\(\begin{aligned} \cos x&=0 \\ x&=\dfrac{\pi}{2},\; \dfrac{3\pi }{2}\end{aligned}\)

And now for the other term:

\(\begin{aligned} 2 \sin x−1&=0 \\ \sin x&=\dfrac{1}{2} \\ x&=\dfrac{\pi}{6},\; \dfrac{5\pi}{6}\end{aligned}\)

Example \(\PageIndex{2}\)

Solve the trigonometric equation \(4 \sin x \cos x+2\cos x−2\sin x−1=0\) such that \(0\leq x<2\pi\).

Solution

Use factoring by grouping.

Figure \(\PageIndex{2}\)

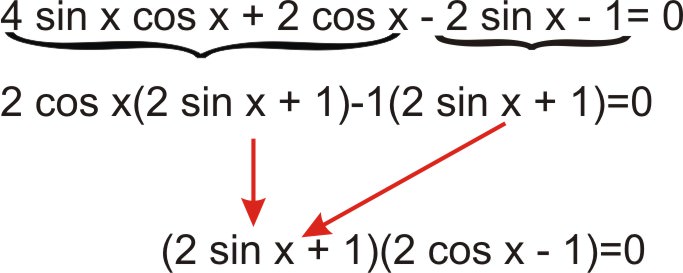
\(\begin{aligned}
2 \sin x+1&=0 & \text { or } \qquad 2 \cos x-1&=0 \\
2 \sin x&=-1 & 2 \cos x&=1 \\
\sin x&=-\dfrac{1}{2} & \cos x&=\dfrac{1}{2} \\
x&=\dfrac{7 \pi}{6},\; \dfrac{11 \pi}{6} & x&=\dfrac{\pi}{3},\; \dfrac{5 \pi}{3}
\end{aligned}\)

Example \(\PageIndex{3}\)

Solve \(\tan^2 x=3\tan x\) for \(x\) over \([0,\pi ]\).

Solution

\(\begin{aligned}
\tan ^{2} x &=3 \tan x & & &\\
\tan ^{2} x-3 \tan x &=0 & & &\\
\tan x(\tan x-3) &=0 & & &\\
\tan x &=0 \qquad \text { or } \quad &\tan x&=3 \\
x &=0, \pi & x&=1.25
\end{aligned}\)

Example \(\PageIndex{4}\)

Find all the solutions for the trigonometric equation \(2 \sin^2\dfrac{x}{4}−3\cos \dfrac{x}{4}=0\) over the interval \([0,2\pi )\).

Solution

\(2\sin^2 \dfrac{x}{4}−3\cos \dfrac{x}{4}=0\)

\(\begin{array}{c} &\qquad \qquad \quad 2\left(1-\cos ^{2} \dfrac{x}{4}\right)-3 \cos \dfrac{x}{4}=0 \\
& \qquad \qquad \quad 2-2 \cos ^{2} \dfrac{x}{4}-3 \cos \dfrac{x}{4}=0 \\
& \qquad \qquad \quad 2 \cos ^{2} \dfrac{x}{4}+3 \cos \dfrac{x}{4}-2=0 \\
&\qquad \qquad \quad \left(2 \cos \dfrac{x}{4}-1\right)\left(\cos \dfrac{x}{4}+2\right)=0 \end{array} \\ \begin{aligned} &\swarrow & \searrow &\\ 2 \cos \dfrac{x}{4}-1&=0 &\text { or } \quad \cos \dfrac{x}{4}+2&=0 \\ 2 \cos \dfrac{x}{4}&=1 & \cos \dfrac{x}{4}&=-2 \\ \cos \dfrac{x}{4}&=\dfrac{1}{2} & & \\ \dfrac{x}{4}=\dfrac{\pi}{3} \quad \text { or } \quad& \dfrac{5 \pi}{3} && \\ x=\dfrac{4 \pi}{3} \quad \text { or }\quad& \dfrac{20 \pi}{3} && \end{aligned}\)

\(\dfrac{20\pi}{3}\) is eliminated as a solution because it is outside of the range and \(\cos x^4=−2\) will not generate any solutions because \(−2\) is outside of the range of cosine. Therefore, the only solution is \(\dfrac{4\pi}{3}\).

Review

Solve each equation for \(x\) over the interval \([0,2\pi )\).

1. \(\cos^2 (x)+2 \cos(x)+1=0\)
2. \(1−2\sin (x)+\sin^2 (x)=0\)
3. \(2\cos (x) \sin (x)−\cos(x)=0\)
4. \(\sin (x) \tan^2 (x)−\sin (x) =0\)
5. \(\sec^2 (x)=4\)
6. \(\sin^2 (x)−2\sin (x) =0\)
7. \(3\sin (x) =2\cos^2 (x)\)
8. \(2\sin^2 (x)+3\sin (x) =2\)
9. \(\tan(x) \sin^2 (x)=\tan(x)\)
10. \(2\sin^2 (x)+\sin (x) =1\)
11. \(2\cos(x)\tan(x)−\tan (x)=0\)
12. \(\sin^2 (x)+\sin (x) =2\)
13. \(\tan(x)(2 \cos^2 (x)+3\cos(x)−2)=0\)
14. \(\sin^2 (x)+1=2\sin (x)\)
15. \(2\cos^2 (x)−3\cos (x)=2\)

Review (Answers)

To see the Review answers, open this PDF file and look for section 3.4.

Vocabulary

Term	Definition
Factoring	Factoring is the process of dividing a number or expression into a product of smaller numbers or expressions.

Additional Resources

Video: Example: Solve a Trig Equation by Factoring

Practice: Trigonometric Equations Using Factoring