18.1: Pre-Trigonometry

Last updated
Save as PDF

Page ID: 4721

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

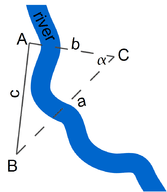
The page at http://www.phy6.org/stargaze/Strig1.htm describes the basic problem of trigonometry (drawing above): finding the distance to some far-away point C, given the directions at which C appears from the two ends of a measured baseline AB. This problem becomes somewhat simpler if:

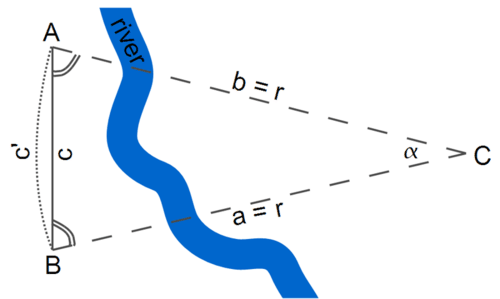
The baseline is perpendicular to the line from its middle to the object, so that \(\Delta ABC\) is symmetric. We will denote its equal sides as \(AB=BC=r\).
The length \(c\) of the baseline \(AB\) is much smaller than \(r\). This means that the angle \(\alpha\) between \(AC\) and \(BC\) is small; that angle is known as the parallax of \(C\), as viewed from \(AB\).
We do not ask for great accuracy, but are satisfied with an approximate value of the distance --- say, within 1%.

The method presented here was already used by the ancient Greeks more than 2000 years ago. They knew that the length of a circle of radius \(r\) was \(2\pi r\), where \(\pi\) (a modern notation, not one of the Greeks, even though \(\pi\) is part of their alphabet) stands for a number a little larger than 3; approximately

\(\pi\approx\,3.14159\ldots\)

Note

The Greek mathematician Archimedes derived \(\pi\) to about 4-figure accuracy, though he expressed it differently, since decimal fractions appeared in Europe only some 1000 years later.

In this case (see Figure above), we can approximate\(\Delta ABC\) as a ‘slice’ of a much bigger circle; in this case, the length of the baseline is approximately equal to the length of the corresponding arc:

\[c\,\approx\,c′\]

There are 360 degrees in a circle and\(\alpha\) degrees in this particular arc; since 360 degrees corresponds to one circumference of arc length (\(2\pi r\)), \(\alpha\) degrees will correspond to an arclength of

\[c′\,=\,\frac{\alpha}{360^o}\times 2\pi r\]

Solving for \(r\) and plugging in \(c\,\approx\,c′\), we find

\[r\,=\,\frac{360^o}{2\pi\alpha}\times c\]

We have solved for \(r\) in terms of \(c\). For instance, if we know that \(\alpha\approx 6^o\) (we'll see why this is relevant later), \(2\pi\alpha\,=\,36^o\) and we get:

\[r\,=\,10c′\]