2.1: Electromagnetic Radiation
- Page ID
- 5650
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A key step in considering the question of life on planets is to understand their energy sources, including energy from the host stars. The energy from stars is powered by nucleosynthesis - the fusion of light elements to form heavier elements (e.g., hydrogen fusion to form helium). A by-product of fusion is the emission of electromagnetic waves, or photon packets of energy. We want to understand how electromagnetic energy varies from star to star, to ultimately understand the impact for life on a planet. In other words, to know the planet, we need to know the star.
Background: the Electromagnetic Spectrum
You may know that a changing electric field will produce a magnetic field. A popular science demonstration in the elementary grades is to wrap a pencil or a nail in a spiral fashion with a wire. When the ends of the wires are connected to the positive and negative poles of a battery, a magnetic field is created. It is critical to wind the wire because that produces a changing direction for the current.
An electromagnetic (EM) wave consists of two perpendicular fields: an electric field and a magnetic field, as shown in the figure below. The changing electric field spawns a changing magnetic field; the changing magnetic field spawns a changing electric field, and voila - the system self-propagates, sailing through space like a thought without a thinker. The electric and magnetic fields are themselves perpendicular to the direction that the wave travels.
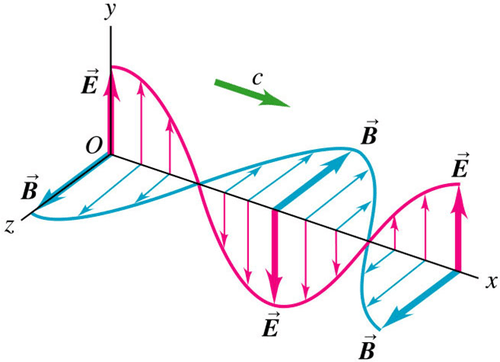
The wavelength, λ, of the EM wave is measured as the distance from peak-to-peak. Visible light is one type of electromagnetic radiation with wavelengths that range from about 400 to 700 nanometers (blue and red light respectively) and is part of the electromagnetic spectrum. The energy of EM radiation scales inversely with wavelength: the shorter the wavelength, the higher the energy. The frequency (\nu\), of EM radiation tells you how many waves go by a particular point each second; the longer the wavelength, the shorter the frequency.
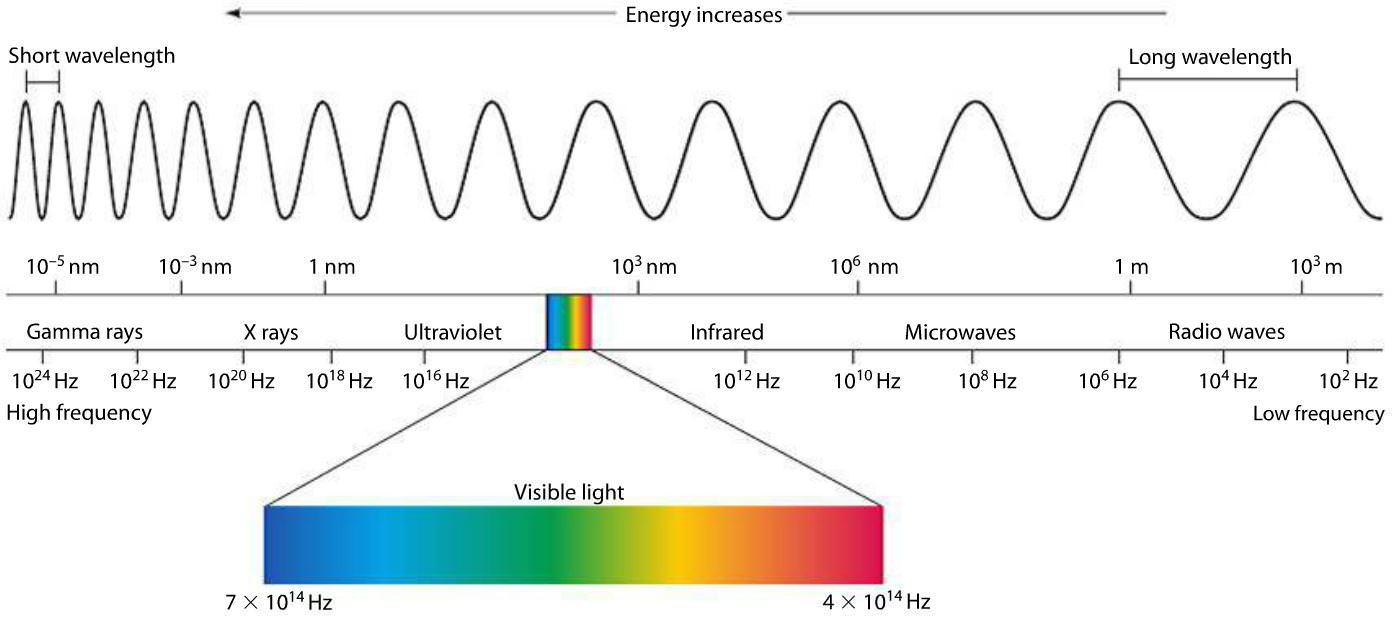
One constant is that all electromagnetic waves travel at the speed of light (c = 3×108 m/s). All EM radiation obeys the mathematical relationship - wavelength times frequency equals the speed of light:
\[\lambda\nu\,=\,c\]
The only difference between red light and blue light is the wavelength (and consequently the energy) of the EM wave. Our brains are tuned to distinguish different wavelengths of light as a phenomenon that we call "color." Likewise, the only difference between radio waves, visible light and X rays is wavelength and hence the energy of the EM wave. Given the broad wavelength range of the EM spectrum, it would seem that our eyes are not very good detectors. Through natural selection and human evolution, the wavelengths of energy that we call visible light coincide with the peak energy emitted from the surface of the Sun and the energy that passes through our atmosphere.
What is the source of energy in the Sun? Nuclear fusion reactions in the cores of stars emit very high energy EM photons - typically gamma rays. The gamma ray photons would travel forever except that the cores of stars are very dense and they interact with that material. Sometimes the gamma ray is scattered and sometimes it is absorbed and re-emitted. Energy must be conserved, however, almost every interaction of EM radiation with matter (the electrons and atoms in the cores of stars) will result in a loss of energy for the incoming photon. Some of that energy can go to accelerating electrons. Or after absorption of the photon by an atom, the higher energy photon (Ein) can be emitted as two lower energy photons. Because of the interaction of energy (high energy gamma rays from the core of the star) with matter, gamma rays ultimately emerge as lower energy light from the surface of the star. In the case of the Sun, the distribution of emerging EM radiation peaks at visible wavelengths.
There are several good online reviews of the physics of EM radiation and you should read through these if you need some additional background material or a refresher. NASA also maintains an nice site describing the electromagnetic spectrum.
Thermodynamics and blackbody radiation
If an object is warmer than its surroundings, it will try to lose that extra energy and come into thermodynamic equilibrium with its surroundings. A glowing ember of coal cools by radiating energy until it reaches the same temperature as it's environment. Ice melts because the energy of the warmer surrounding air raises the temperature of the ice. The laws of thermodynamics are strictly enforced and stars are one of nature's most powerful energy sources. An object in thermal equilibrium (by definition) is not warming up or cooling down - it maintains a constant temperature.
Hypothetical bodies in thermal equilibrium are historically called "black bodies" because they do not reflect any light. However, a blackbody will emit a spectrum of light. For example, humans emit light at infrared wavelengths ("heat"). With this simplistic assumption, stars can be considered to approximate a black body: they are in thermal equilibrium, they do not reflect light, they emit a spectrum of light that is reasonably well-described by Planck's equation below for a black body:
\[B_{\lambda}\,=\frac{8\pi\,hc}{\lambda^5(e^{\frac{hc}{\lambda kT}}-1)}\]
In equation (2):
- Bλ is the energy of the body at various wavelengths
- λ is the wavelength
- h=6.626×10−34 m2kg/s is Plancks constant
- k=1.3806×10−23 m2kgs−2K−1 is the Boltzmann constant
- c=2.99×108 m/s is the speed of light
- T is the temperature of the object
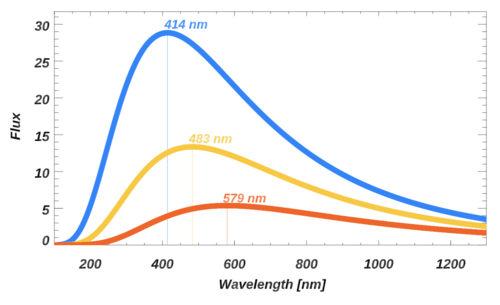
Using equation (2), thermal energy curves have been calculated for three temperatures: 7000K, 6000K, and 5000K. For reference the Sun has a temperature of about 5800 K, so these are energy distributions representative of a slightly warmer (more massive) star than the Sun and a slightly cooler (less massive) star. There are a few things to notice about these energy distributions:
- All of these bodies emit EM radiation with a distribution of photon energies, not photons with a single energy.
- The hottest object (blue curve) has the most intense signal and the peak of that curve is shifted to slightly shorter wavelengths.
- The other curves are all nested under the blue curve. That is, the intensity of energy (flux is the luminosity per unit area) emitted by the 6000 K object (gold curve) is less than the intensity of the 7000 K object and the intensity of the 5000 K object (red curve) is lower than the two hotter objects. This calculation implicitly assumes that all 3 objects are the same size. However, if the cooler object is an evolved red giant star, it will have an expanded radius - in this case, the shape of the curve will be the same as indicated by Eqn (2), but the intensity will scale up and could be greater than the flux of the hotter stars because the size of the star is larger.
- The numbers at the peak of each curve indicate the wavelength where the peak flux occurs. The hotter star emits the maximum amount of energy at bluer wavelengths than the cooler stars.
All objects with thermal energy radiate a spectrum of energy with different intensity (strength) at different wavelengths given by equation (2). The shape of the blackbody curve is determined by the temperature of the blackbody.
Wien's Law
Wien's law relates the characteristic temperature of a blackbody to the wavelength where the peak energy is emitted:
\[\lambda_{max}\,=\frac{2.898\,x\,10^6[K\cdot nm]}{T[K]}\]
Equation (3) says that if you know the temperature of an object, you can predict the peak wavelength (or color) of the object. Conversely, if you measure the peak wavelength, you can derive the blackbody temperature of the object with Wien's law.
Flux and Luminosity
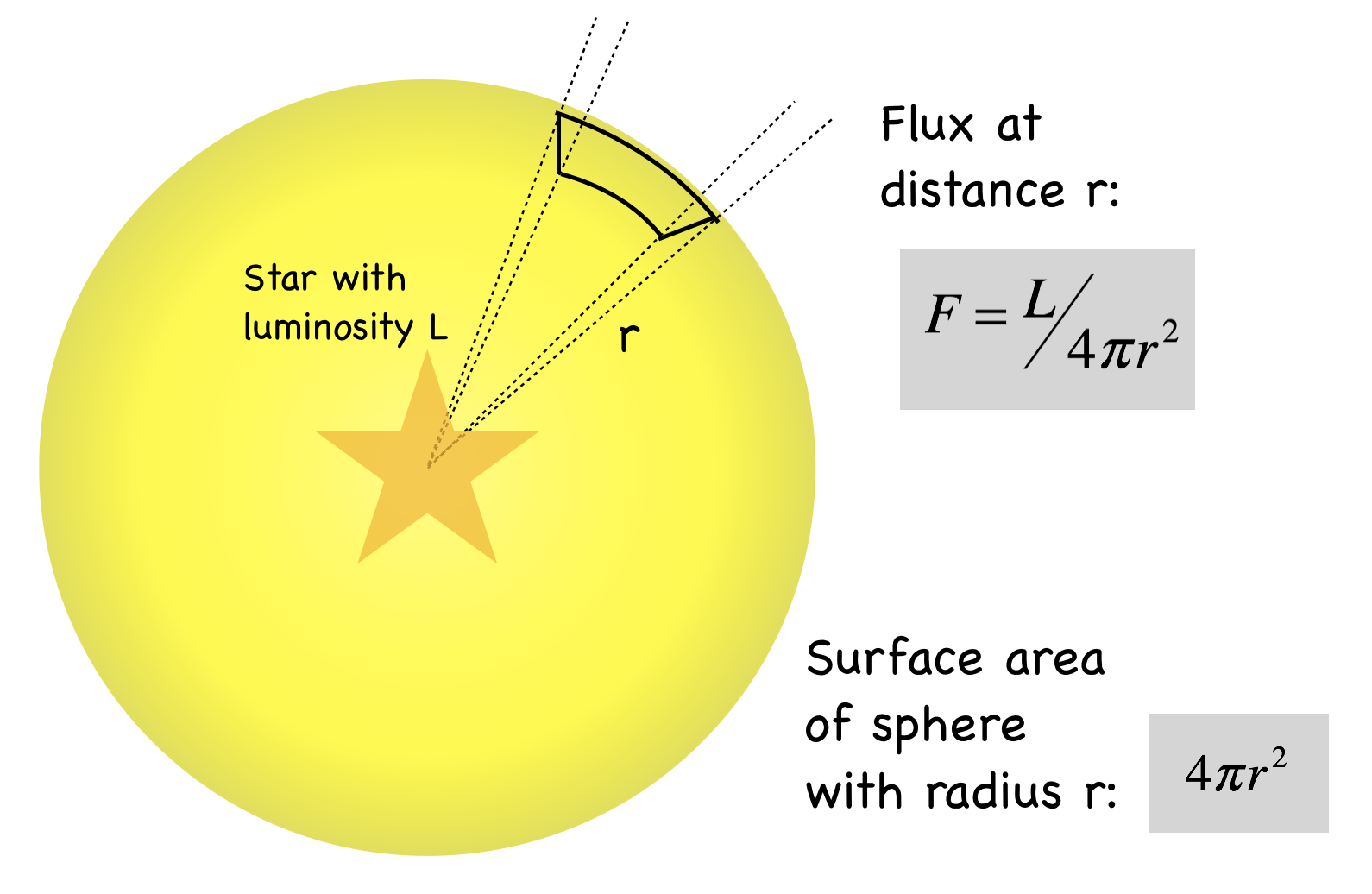
Luminosity is the total amount of energy that an object (like a star) puts out each second. It has dimensional units of energy per second. In the same way that a 100 W bulb will always put out 100 Watts whether we are standing close or farther away, the luminosity of a star does not depend on our distance from it.
However, astronomers do not measure luminosity, they measure flux: the luminosity that is intercepted by a detector such as a photographic plate or a digital camera. If you imagine a spherical surface - a bubble - around a star, then the luminosity is the integrated (total) light from the surface of that bubble. The flux, which is the luminosity per unit area, decreases as the surface area of the spherical volume increases. This is the same phenomenon that happens with expanding balloons. The balloon has a certain amount of material, usually latex or rubber. Analogous to luminosity, that amount of material is constant, no matter how much air is in the balloon. However, as the balloon expands, that constant amount of material is stretched over a larger surface area. The walls of the balloon get thinner and the amount of material per unit area decreases. The luminosity of a star is constant. The flux that we measure depends on whether we are "up close" or far away from the star.
Stefan-Boltzmann Law
An object in thermal equilibrium maintains a constant temperature - it neither warms up or cools down. The Stefan-Boltzmann law relates the flux that is radiated by a blackbody to the equilibrium temperature of that body.
\[F\,=\sigma\,T^4Jm^{-2}s^{-1}\]
In this equation:
- F is the radiated energy per unit area per unit time (the flux)
- σ=5.67×10−8 J s−1m−2 K−4 is the Stefan-Boltzmann constant
- T is the equilibrium temperature of the object in degrees Kelvin

We can relate the luminosity of a star to the flux and therefore to the temperature of the star at a particular distance, r :
\[L\,=\,F4\pi r^2\,=\,\sigma T^44\pi r^2\]
We get to choose "r" for the particular situation we are investigating. We might want "r" to be the radius of the star - in this case we would be defining the temperature at the surface of the star. Or we might want "r" to be the orbit of the Earth - in this case, we would be solving for the temperature from solar radiation at the distance of the Earth. In both of those cases (r = the radius of the star; r = the orbit of the Earth), if we integrate (or "add up") the flux on the surface of a sphere at that distance, the total equals the luminosity of the star.
Luminosity, flux, temperature and radius
Equation (5) tells us that if the temperature of the star doubles, the luminosity increases by a factor of 16 (2*2*2*2). If the radius of a star doubles but the temperature stays the same, the luminosity increases by a factor of four. If the radius increases by a factor of two and the temperature decreases by a factor of two, how does the luminosity of the star change according to equation 5?

