1.10: X. Making Connections to Educational Policies
- Page ID
- 15111
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)10
X. Making Connections to Educational Policies
Emily van Zee and Elizabeth Gire
What does it mean to do science? What should every person know about science? How should science be taught? These are questions that every community decides by what and how children learn science, or not, in its schools.
This section completes this unit. As an informed citizen, you should become aware of your community’s standards for teaching science, particularly if you are a teacher, preparing to become a teacher, or a parent advocating for more science to be taught in elementary schools.
Question 1.25 What are the current standards for teaching science at various grade levels in your community?
- Contact the department of education in your community to find out about the current standards for teaching science at various grade levels. The Oregon Department of Education’s announcement, for example, is at https://www.oregon.gov/ode/educator-resources/standards/science/Pages/Science-Standards.aspx . This state adopted the US Next Generation Science Standards (NGSS Lead States, 2013) in 2014.
A. Learning about the US Next Generation Science Standards: Science and engineering practices
The Next Generation Science Standards (NGSS) website is at https://www.nextgenscience.org . This website describes three dimensions of what it means to be proficient in science and engineering. These dimensions are science and engineering practices, crosscutting concepts, and disciplinary core ideas that NGSS recommends for students to learn at various grade levels.
This unit began, for example, with the scientific practice of asking questions about the nature of light such as How does light seem to travel from a source to a screen? By exploring light and shadows, students developed a model for thinking about light, that light can be envisioned as rays traveling in straight lines. Students next used that model to explain the cause of a surprising effect, that the projection on the screen of a pinhole camera is upside down. Searching for the cause of an effect is a crosscutting concept characteristic of the many domains of science and engineering. During explorations in this unit, students inferred and used a disciplinary core idea that objects can be seen when light reflected from their surfaces enters our eyes.
Development of the Next Generation Science Standards was based on an earlier document, A Framework for K-12 Education: Practices, Crosscutting Concepts, and Core Ideas (https://www.nap.edu/read/13165/chapter/1). The NGSS website includes a series of appendices that discuss various aspects of the Framework’s recommendations.
- NGSS Appendix F describes eight scientific and engineering practices at https://www.nextgenscience.org/resources/ngss-appendices . Scan these to see what they are and read about any that you find particularly interesting.
- Complete Table I.4 by indicating with a check mark your perception of participating in some way in some of the eight NGSS science and engineering practices during your exploration of light phenomena.
| Table I.4. Science and engineering practices (NGSS Lead States, 2013) | |||
|---|---|---|---|
| Practices | Exploring light and shadows | Exploring pinhole phenomena and estimating the size of an object | Exploring reflection, refraction, dispersion and explaining rainbows |
| 1. Asking questions (for science) and defining problems (for engineering | |||
| 2. Developing and using models | |||
| 3. Planning and carrying out investigations | |||
| 4. Analyzing and interpreting data | |||
| 5. Using mathematics and computational thinking | |||
| 6. Constructing explanations (for science) and designing solutions (for engineering) | |||
| 7. Engaging in argument from evidence | |||
| 8. Obtaining, evaluating, and communicating information | |||
- Provide an example by choosing one of the practices and describe how you did this.
Complete your entries into Table I.4 and description of participating in one of the practices before reading an example of student work.
1. Example of student work about relevant educational policies
As shown in Fig. 1.55, a student indicated that many of the NGSS science and engineering practices had been used during this unit.
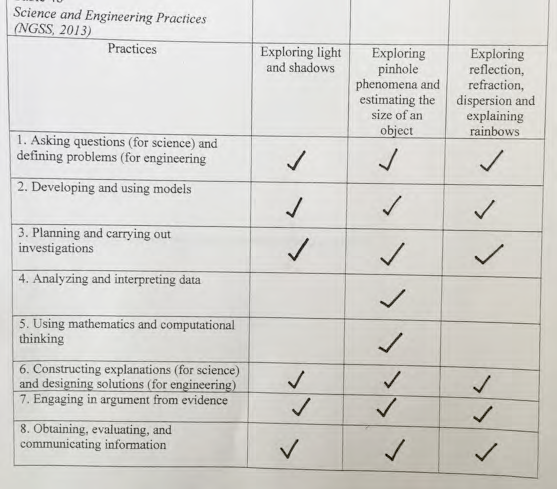
(The table) indicates with a check mark my perception of participating in some way in some of the eight practices specified during my exploration of light phenomena…One of the practices that we have participated in during class is developing and using models and we did this when we developed the idea that light can be envisioned as rays traveling in straight lines. In order to do this, we used a lamp, a barrier, a white piece of paper, and a meter stick. The light shined directly on the barrier, so the barrier made a shadow on the white paper. The meter stick was placed at the edge of the lamp and it went straight past the edge of the barrier. The meter stick represents a ray of light traveling from the lamp. The shadow of the meter stick was lined up with the edge of the barrier’s shadow on the paper, which we inferred means that the light travels in a straight line because the shadows lined up perfectly in relation to the actual objects, so we assume that light can always be envisioned as rays traveling in straight lines. Developing and using a model allowed us to develop a very important idea.
Physics student, Spring 2016
B. Reflecting upon this exploration of light phenomena
This unit began with exploring light and shadows in order to develop ways to think and talk about the nature of light. The first demonstration involved turning on a lamp in a dark room and observing light shining all around on the ceiling, the floor, and people’s faces. The first central idea to emerge from discussing this demonstration likely seemed obvious, that light leaves a source in all directions. This central idea needed refinement, however, to acknowledge that directional sources like lasers exist and that not all directions might occur. The refined central idea became light leaves most sources in many directions. Small group explorations with a light source, barrier, and screen included using a meter stick (or ruler) to serve as a physical model representing the central idea that light can be envisioned as rays traveling in straight lines.
These two central ideas formed a conceptual model useful in explaining an intriguing phenomenon: if one looks at a light bulb through a pinhole camera, the projection of the light bulb is upside down! A good way to start thinking about such puzzling phenomena is to make a sketch of the situation, in this case, to draw a picture of the light bulb and a picture of its upside-down projection. The next step is to think about what one knows that is relevant to the situation shown in the sketch. For example, how can envisioning light as rays leaving a source in straight lines help here? In particular, how can the physical model, the meter stick (or ruler), help to think about how light from the top of the light bulb can travel through the pinhole toward the bottom of the screen?
Laying one end of the meter stick (or ruler) near the sketch of the top of the bulb and the other end of the meter stick (or ruler) near the sketch of the bottom of the projection suggests a useful insight: that if light rays from any point on the bulb can be envisioned as leaving the source in many directions, some rays from the top of the bulb can be thought of as traveling straight through the pinhole toward the bottom of the screen; some rays from the middle of the bulb can be thought of as traveling straight through the pinhole to the middle of the screen; and some rays from the bottom of the bulb can be thought of as traveling straight through the pinhole toward the top of the screen. This insight implies that an alternative explanation is not needed, that something happens to the rays to “flip” the projection. The physical model of the meter stick (or ruler) suggests that nothing happens to the rays forming the projection; they just keep traveling in the same direction they happen to be going, straight through the pinhole. The aluminum foil around the pinhole blocks other rays from the source from shining on the screen.
Simplifying a sketch can help make important aspects of a situation more prominent. Drawing a vertical line representing the bulb and a parallel vertical line representing an upside-down projection, for example, provides a useful visual model for pinhole phenomena, the ray diagram. Tracing the rays with one’s finger while telling the story represented by a ray diagram can be a compelling way to communicate to others what one is envisioning to be happening.
The ray diagram for pinhole phenomena consists of two similar triangles. Interpreting these geometrically leads to a mathematical model for pinhole phenomena, an algebraic equation that expresses the direct relationship between ratios of the corresponding lengths of the similar triangles. This mathematical model made possible estimating a quantity that could not be directly measured. Students held a pinhole in a sheet of aluminum foil one meter away from a screen, traced the Sun’s projection on the screen, measured the diameter of the projection, and used the equal ratios of corresponding lengths of similar triangles as well as information about the distance from the Earth to the Sun to estimate the Sun’s diameter.
Exploring reflection phenomena with a mirror and two meter sticks or rulers in a dark room prompted a refinement of this ray model for light. Light rays can be envisioned as traveling in straight lines until they hit a mirror and bounce away, with the angle of reflection equaling the angle of incidence. Balls also bounce off walls and floors in this way, which suggests an elaboration of this model for light, that rays can be envisioned as an on-going flow of particles, called photons, in straight lines. An alternative model, representing light as waves, also can be helpful in explaining complex phenomena, as discussed in Unit 4.
Exploring refraction and dispersion phenomena prompted an additional refinement of this conceptual ray model for light. When light rays move from one medium into another, such as from air into water or from water into air, the rays can be envisioned as traveling in straight lines that bend at the point of entering or leaving a medium. White light from the Sun can be envisioned as composed of many colors, with the degree of bending related to the color of the ray. This refined conceptual model of light was powerful in explaining a complex phenomenon: rainbows!
C. Making connections to NGSS understandings about the nature of science
This unit has provided many examples of the nature of science as articulated in Appendix H of the Next Generation Science Standards (NGSS, Lead States, 2013) https://www.nextgenscience.org/resources/ngss-appendices . Appendix H includes tables that provide insights about the development of these understandings about the nature of science across grade spans of K-2, 3-5 (elementary), 6-8 (middle school), and 9-12 (high school). Four NGSS understandings about the nature of science are related to the science and engineering practices.
One NGSS understanding about the nature of science, for example, is that scientific investigations use a variety of methods. Children in grades K-2, for example, should understand that scientists use different ways to study the world. In this unit, for example, students have made observations using lamps, barriers, pinhole cameras, mirrors, cups of water, and prisms to explore what happens when light moves from one place to another.
Another NGSS understanding is that scientific knowledge is based on empirical evidence. Students in grades 3-5, for example, should learn that science findings are based on recognizing patterns. In this unit, for example, students have explored patterns in what happens to shadows when someone moves a barrier closer or farther away from a light source.
Students experience in several ways the NGSS understanding that scientific knowledge is open to revision in light of new evidence. Students in grades 6-8 (middle school), for example, should learn that science explanations are subject to revision and improvement in light of new evidence. In this unit, the central idea that light can be envisioned as rays traveling in straight lines, for example,was modified as the students explored what happens when light reflects from a mirror, refracts when entering and leaving a new material, and disperses if the light is composed of more than one color
K-8 development of the NGSS understanding that science models, laws, mechanisms, and theories explain natural phenomena ranges, for example, from scientists use drawings, sketches, and models as a way to communicate ideas (K-2) to sciencetheories are based on a body of evidence developed over time (middle school). In this unit, for example, students have learned how to use ray diagrams and central ideas based on evidence to explain a variety of phenomena. They also have had access to original descriptions of investigations of light conducted over several centuries.

