4.2: Historical and Current Tax Issues
- Page ID
- 6937
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Historical & Current Tax Issues
The most current tax issues revolve around the idea that taxes are too high and that the tax laws should be much simpler. Some current concepts are to create value-added taxes, or a flat tax on individual income, or create more progressive tax brackets. Politicians and government officials revise taxes depending on the social and economic goals of their administrations, therefore tax laws can change from year to year and may either increase or decrease taxes on individuals, businesses or corporations.
Universal Generalizations
- The consequence of tax reform was to make the individual tax code more complex than ever.
- Taxes influence the economy by affecting resource allocation, consumer behavior, and the nation’s productivity and growth.
- Taxes are the single most important way for the government to raise revenue.
- Government economic policies at all levels influence levels of employment, output, and price levels.
Guiding Questions
- How do the changing government policies of taxing affect the economy?
- What are the positive and negative aspects of taxation?
- How do taxes create a burden for the taxpayer?
The Kennedy Tax Cut of 1964
Now that we have some basic idea of how income taxes work, we turn to the Kennedy tax cut of 1964. We begin with some background information; we then develop the economic tools needed to analyze the effects of the tax policy on household consumption and therefore on real gross domestic product (real GDP).
In his inaugural presidential address, President Kennedy famously said, “My fellow Americans, ask not what your country can do for you; ask what you can do for your country.” The Kennedy administration recruited top individuals in all fields (“the best and the brightest”) to come to Washington in this new spirit of commitment to public service.
Every president has a group of economists that are known as the Council of Economic Advisors (CEA: Council of Economic Advisors). They provide advice on economics and economic policy. The list of members and staff of the 1961 CEA reads today like a “who’s who” of economics. James Tobin and Robert Solow were prominent members of the economics team; both went on to win the Nobel Prize in Economics. The chairman of the CEA was Walter Heller, an economist known for a wide variety of contributions on the conduct of macroeconomic policy.
The economists in the Kennedy administration observed that there had been three recessions in the two Eisenhower administrations (1952–1960): one from 1953 to 1954 after the Korean War, one from 1957 to 1958, and one in 1960. You can see these in Figure 1:. The CEA members and staff thought that more aggressive fiscal and monetary policies could be used to keep the economy more stable and prevent such recessions. Their goal of moderating fluctuations in the economy was based on the framework of the basic aggregate expenditure model, which had been developed in the aftermath of the Great Depression, modified by some developments in economic thinking from the 1940s and 1950s. Based on that analysis, they believed that fiscal and monetary policies could be used to control aggregate spending and hence real GDP.
Figure 1: Real GDP in the 1950s
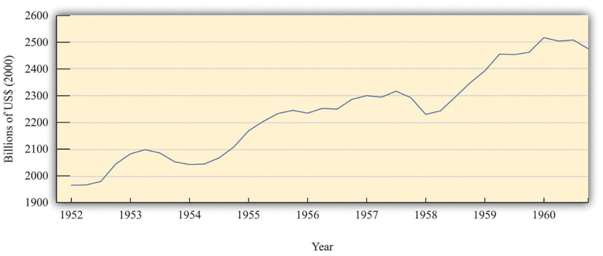
Source: Bureau of Economic Analysis.
The chart shows real GDP in the United States between 1952 and 1960, measured in billions of year 2000 dollars.
This group of economists had, on one hand, a clearly defined goal of stabilizing the macroeconomy, and on the other hand, a set of policy instruments—economic variables such as taxes, government spending, and interest rates—that were under the control of policymakers. They also had a framework of analysis (the aggregate expenditure model) that explained how these instruments could be used to achieve their goals. Finally, they had a president who was willing to listen and take their advice. Never before had economists had such tools and wielded such influence.
The opportunity to test their ideas arose toward the middle of the Kennedy presidency. In the middle of 1962, it was apparent to the Kennedy administration economists that the economy was beginning to sputter. The growth rate of real GDP was 7.1 percent in 1959 but decreased to 2.5 percent and 2.3 percent in 1960 and 1961, respectively. Their response was to initiate a tax cut.
As is usually the case when a major fiscal policy action is under consideration, there was a lengthy time lag between the initiation of the policy and its implementation. Even though the tax cut was proposed in 1962, President Kennedy never saw it put into effect. He was assassinated in November 1963; the tax cut for individual households and corporations was not enacted until early 1964. For households, tax withholding rates decreased from 18 percent to 14 percent, leading to an estimated tax reduction of about $6.7 billion. Taxes on corporations were also decreased; the reduction in taxes for 1964 was expected to be about $1.7 billion. By 1965, the economists expected that taxes would be lower by $11 billion. In 1965, nominal GDP was about $719 billion, so these changes were about 1.5 percent of nominal GDP.
For many observers of the macro-economy, this was a watershed event. The Economic Report of the President proclaimed 1965 the “Year of the Tax Cut.” In retrospect, these years were the heyday of Keynesian macroeconomics: for the first time, the government was using tax policy in an attempt to fine-tune the economy.
Figure 2: shows what happened to average and marginal tax rates. Marginal tax rates were very high at the time—much greater than in the present day. At high levels of income, more than 90 cents of every additional dollar had to be paid to the government in taxes. Consequently, average tax rates were also high: an individual with taxable income of $100,000 (a very high level of income back then) had to pay about two thirds of that amount to the government. The Kennedy tax cuts reduced these tax rates. Even after the tax cut, the marginal and average tax rates both increased with income. In other words, the tax system still redistributed income across households. But when we compare 1963 and 1964, we see that the marginal tax rate did not increase as rapidly under the new tax policy. Therefore, this channel of redistribution was weaker under the new tax policy.
Figure 2: Tax Policy During the Kennedy Administration
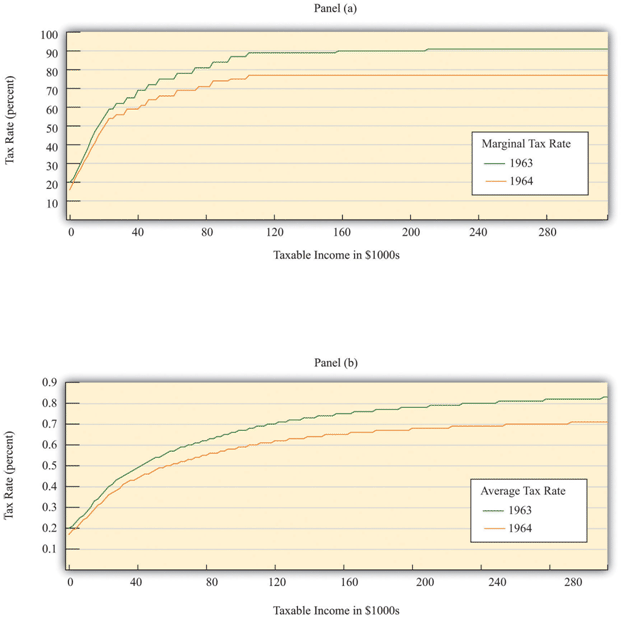
Source: Department of the Treasury, IRS 1987, “Tax Rates and Tables for Prior Years” Rev 9-87
The charts show the impact of the Kennedy tax cut. Part (a) highlights how the marginal tax rates for households changed from 1963 to 1964, and part (b) shows the impact on average tax rates. For their policy to be successful, Kennedy’s advisors had to ask and then answer a series of questions. How big a tax cut should they recommend? How long should it last? What would be the effect on government revenues? What would be the effect on real GDP and consumption? Economists working in government today confront exactly the same questions when contemplating changes in tax policy. Questions such as these epitomize economics and economists at work.
Looking back at this experiment with almost half a century of hindsight, we can ask additional questions. How well did these policies work in terms of achieving their goal of economic stabilization? What actually happened to consumption and output? Was the tax policy successful?
The Kennedy economists needed a quantitative model of economic behavior: a formalization of the links between their policy tools (tax rates) and the outcomes that they cared about, such as consumption and output. Using the aggregate expenditure model, they wanted to know how big a change in real GDP they could expect from a given change in the tax rate. To use the model to study income taxes, we need to add some theory about how spending responds to changes in taxes. Accordingly, we study the effects of income taxes on household consumption and then discuss how changes in consumption lead to changes in output.
Although we are using a historical episode to help us understand the effect of taxes on the economy, this chapter is not intended as a lesson in economic history. Variations of this same model are still used today to analyze current economic policies. Indeed, in response to the economic crisis of 2008, many countries around the world cut taxes in an attempt to stimulate their economies. By studying the experience of the early 1960s, we gain insight into a critical part of macroeconomics: the linkage between consumption and output.
Having said that, economics has advanced significantly since the 1960s, and the state-of-the-art analysis for that time seems oversimplified today. Modern economists think that the policy advisers in the 1960s neglected some key aspects of the economy. Their insights were not wrong, but they were incomplete. Our understanding of the economy has evolved since Tobin, Solow, and Heller designed the nation’s tax policy.
Household Consumption
We begin by studying the relationship between consumption and income. We first develop some ideas about how households make consumption decisions, and, on the basis of those ideas, we make some predictions about what we expect to happen when there is a cut in taxes. We then examine the evidence from the Kennedy tax cut.
Income, Consumption, and Saving
Interested in studying, say, the market for ice cream? Examine how households choose between ice cream and other products that are close substitutes, (such as frozen yogurt), and between ice cream and other products that are complements, (such as hot fudge sauce). When studying microeconomics, however, we focus on choices for goods made at a particular point in time. In microeconomics, we study how a consumer allocates incomes across a wide variety of products.
Macroeconomics has a different emphasis. It emphasizes the choice between consumption and saving. Instead of thinking about the consumption of ice cream today versus frozen yogurt today, we study the choice between consumption today and consumption in the future. To highlight this decision, macroeconomists downplay the choices among different goods and services. Of course, in reality, households decide both how much to spend and how much to save, and what products to purchase. But it is convenient to treat these decisions separately.

The same basic ideas of household decision making apply in either case. Households distribute their income across goods to ensure that no redistribution of that spending would make them better off. This is true whether we are talking about ice cream and frozen yogurt, or about consumption and saving. Households allocate their income between consumption and savings in a way that makes them as well off as possible. They do not spend all their income this year because they want to save some for consumption in the future.
Suppose a household in the United States had taxable income of $20,000 in 2010. Some of this income goes to the payment of taxes to federal and state governments. (From our earlier discussion, the average federal tax rate is 13.25 percent.) The rest is either spent on goods and services or saved. The income that is spent on goods and services today is spread over the many products that a household buys. The income that is saved will likewise be used in the future to purchase different goods and services.
Personal Income and Disposable Income
The most basic measure of aggregate economic activity is real GDP, which is the total amount of final goods and services produced in our economy over a period of time, such as a year. The rules of national income accounting mean that real GDP measures three different things at once: the production or output of the economy, the spending in the economy; and the income generated in the economy. We use real GDP as our most general measure of income.
We work in this chapter with two further concepts of income from the national accounts: personal income and disposable income. Some of the income generated in the economy is retained by firms to finance new investment, so it does not go to households. Personal income refers to that portion of GDP that finds its way directly into the hands of households. (At the level of an individual household, it corresponds closely to adjusted gross income on the tax form.) Disposable income is what remains after we subtract from personal income the taxes paid by households to the government and add to personal income the transfers (such as welfare payments) received by households from the government. For a household, disposable income measures its available resources after taxes have been paid and transfers received.
Consumption Smoothing
Our starting point for understanding consumption choices is the household budget constraint for a typical household. The household receives income from working and other sources and pays taxes to the government. The remainder is the household’s disposable income. The household budget constraint reminds us that, ultimately, you must either spend the income you receive or save it; there are no other choices. That is, disposable income = consumption + saving.
A theory of consumption is a theory of how households decide to divide their income between consumption and saving. Saving is a way to convert current income into future consumption. A theory of consumption is equivalently a theory of saving. A fundamental idea about household behavior is that people do not wish their consumption to vary a lot from month to month or year to year. This principle is so important that economists give it a special name: consumption smoothing. Households use saving and borrowing to smooth out fluctuations in their income and keep their consumption relatively smooth. People will tend to save when their income is high and will dissave when their income is low. (Dissave is the word economists use to mean either running down one’s existing wealth or borrowing against future earnings.)
Perfect consumption smoothing means that the household consumes exactly the same amount in each period of time (for example, a month or a year). If a construction worker earns $10,000 per month working from May to October but nothing for the rest of the year, we do not expect that he will spend $10,000 per month in the summer and then starve in the winter. It is much more likely that he will save half of his income in the summer and spend those savings in the winter so that he spends about $5,000 per month throughout the year.
The logic of consumption smoothing is the same as the argument for why households buy many different goods rather than one single good. Households typically take their income and spend it on a wide variety of products. Furthermore, when income increases, the household will spread this extra income across the spectrum of goods it consumes; not all of it is spent on one good. If you obtain more income, you do not spend all this extra income on ice cream, for example. You buy more of many different goods.
The Consumption Function
One way to represent consumption smoothing is by means of a consumption function. This is an equation that relates current consumption to current disposable income. It allows us to go from an abstract idea about consumption behavior—consumption smoothing—to a specific formulation of consumption that we can use in a model of the aggregate economy.
We suppose the consumption function can be represented by the following equation:
consumption = autonomous consumption + marginal propensity to consume × disposable income
make three assumptions:
- Autonomous consumption is positive. Households consume something even if their income is zero. If the household has accumulated a lot of wealth in the past or if the household expects its future income to be larger, autonomous consumption will be larger. It captures both the past and the future.
- We assume that the marginal propensity to consume is positive. The marginal propensity to consume captures the present; it tells us how changes in current income lead to changes in current consumption. Consumption increases as current income increases; the larger the marginal propensity to consume, the more sensitive current spending is to current disposable income. By contrast, the smaller the marginal propensity to consume, the stronger is the consumption-smoothing effect.
- We also assume that the marginal propensity to consume is less than one. This says that not all additional income is consumed. When the household receives more income, it consumes some and saves some. The marginal propensity to save is the amount of additional income that is saved; it equals (1 – marginal propensity to consume).
Table 1 contains an example of a consumption function where autonomous consumption equals 10,000 and the marginal propensity to consume equals 0.8. If the household earns no income at all (disposable income = $0), it still spends $10,000 on consumption. In this case, savings equal −$10,000. This means the household is either drawing on existing wealth (accumulated savings from the past) or borrowing against income expected in the future. The marginal propensity to consume tells us how the household divides additional income between consumption and saving. In our example, the household spends 80 percent of any additional income and saves 20 percent.
| Disposable Income ($) | Consumption ($) | Saving ($) |
| 0 | 10,000 | −10,000 |
| 10,000 | 18,000 | −8,000 |
| 20,000 | 26,000 | −6,000 |
| 30,000 | 34,000 | −4,000 |
| 40,000 | 42,000 | −2,000 |
| 50,000 | 50,000 | 0 |
| 60,000 | 58,000 | 2,000 |
| 70,000 | 66,000 | 4,000 |
| 80,000 | 74,000 | 6,000 |
| 90,000 | 82,000 | 8,000 |
| 100,000 | 90,000 | 10,000 |
For example, when income is equal to $20,000, consumption can be calculated as follows:
consumption = $10,000 + 0.8 × $20,000
= $10,000 + 0.8 × $20,000
= $26,000.
The household is still dissaving but now only by $6,000. Table 1 also shows that when income equals $50,000, consumption and income are equal, so savings are exactly zero. At income levels above $50,000, the household has positive savings.
Figure 3 shows the relationship between consumption and income graphically. We also graph the savings function in Figure 3. The savings function has a negative intercept because when income is zero, the household will dissave. The savings function has a positive slope because the marginal propensity to save is positive.
Figure 3: Consumption, Saving, and Income
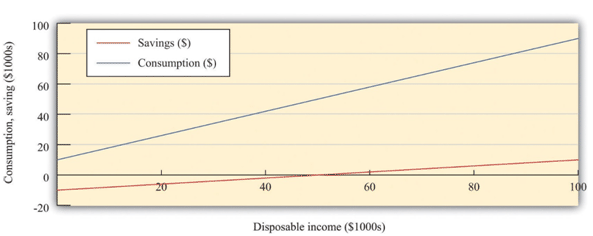
The graph shows the relationship between consumption and disposable income, where autonomous consumption is $10,000 and the marginal propensity to consume is 0.8. When disposable income is below $50,000, savings are negative, whereas at income levels above $50,000, savings are positive. As well as the marginal propensity to consume and the marginal propensity to save, we can examine the average propensity to consume, which measures how much income goes to consumption on average. It is calculated as follows:
average propensity to consume = consumption /disposable income
When disposable income increases, consumption increases but by a smaller amount. This means that when disposable income increases, people consume a smaller fraction of their income: the average propensity to consume decreases. In terms of mathematics, we are saying that, if we divide through the consumption function by disposable income, we get
Consumption = autonomous consumption + marginal propensity to consume
disposable income disposable income
An increase in disposable income reduces the first term and the average propensity to consume. Meanwhile, the ratio of saving to disposable income is called the savings rate. For example,
savings rate = savings disposable income.
The savings rate and the average propensity to consume together sum to 1. In other words, a decline in the average propensity to consume equivalently means that households are saving a larger fraction of their income.
Because the consumption and savings relationships are two sides of the same coin, economists wishing to find the actual values of autonomous consumption and the marginal propensity to consume can examine data on consumption, savings, or both. If the data were perfect, we would get the same answer either way. For the United States, both consumption and savings data are readily available, but in some countries the data on savings may be of higher quality than the consumption data, in which case economists use savings data to understand consumption behavior.
Some Warnings about the Consumption Function
The consumption function is useful because it captures two fundamental insights: households seek to smooth their consumption, but consumption nonetheless responds to current income. But the consumption function is really too simple.
First, it ignores the role of accumulated wealth. If you consider two households with the same level of current income but different amounts of accumulated wealth, the one with higher wealth will probably consume more. Second, the consumption function does not explicitly include the role of expectations. A household’s consumption reflects not only income today and the accumulation of income in the form of wealth but also anticipated income. So, for example, if a government announces that it will increase income tax rates in two years, we expect that households will respond immediately to smooth out the effects of these future taxes. The only way the consumption function allows us to capture wealth or expectations of future income is through autonomous consumption. This is fine as far as it goes, but it means that we are taking too many aspects of consumption as given, rather than explaining them with our theory.
Another complication is that changes in income today are often correlated with changes in income in the future. If your income increases today, is this an indication that your income will also be higher in the future? To see why this matters, consider two extreme examples. First, suppose that you receive a one-time inheritance of $10 million. What will you do with this income? According to the consumption smoothing argument, you will save some of this income to increase your consumption in the future. Roughly speaking, if you thought you had 10 years left to live, you might increase your consumption by about $1 million per year. In this case your marginal propensity to consume would be only 0.1.
Now suppose that instead of a $10 million windfall, you learn you will receive $1 million each year for the next 10 years. In this case, your income is already spread out over your lifetime. So, in this second case, you will again want to smooth your consumption. But since the increase in income will be maintained for your lifetime, you can increase your consumption by an amount equal to the increase in your income. Your marginal propensity to consume will be 1.0.
The difference between these two situations is that in the first case the income increase is temporary, and in the second it is permanent. The logic of consumption smoothing implies that the marginal propensity to consume is near 1 for permanent changes in income but much smaller for temporary changes in income.
The Effects of a Change in Income Taxes
We can now figure out the effects of a cut in taxes on consumption and saving. A reduction in taxes will increase disposable income. From the consumption function, this results in an increase in consumption equal to the marginal propensity to consume times the increase in disposable income. The average propensity to consume decreases. To summarize, if taxes are cut in the economy, we expect to see the following:
- An increase in disposable income
- An increase in consumption that is smaller than the increase in disposable income (that is, a marginal propensity to consume less than 1)
- A decline in the average propensity to consume
When natural scientists such as molecular biologists or particle physicists want to see how good their theories are, they conduct experiments. Economists and other social scientists have much less ability to carry out experiments—certainly at the level of the macroeconomy. The Kennedy tax cut, however, is like a “natural” experiment in that there was a major policy change that we can think of as a change in an exogenous variable. It is not, in truth, completely exogenous. We already explained that the tax cut was enacted in response to the poor performance of the economy. We are not badly misled by thinking of it as an exogenous event, however. We can therefore use it to see how well our theory performs. Specifically, we can look to see whether disposable income and consumption do behave as we have predicted.
Empirical Evidence on Consumption
Before we turn to those specific questions, let us examine some data on consumption.
Figure 4 shows the behavior of consumption and disposable income from 1962 to 2010. The measures of both income and consumption are in year 2005 dollars. This means that the nominal (money) levels of income and consumption for each of the years have been corrected for inflation, so that we can see how the real level of consumption relates to the real level of income.
Figure 4: Consumption and Income
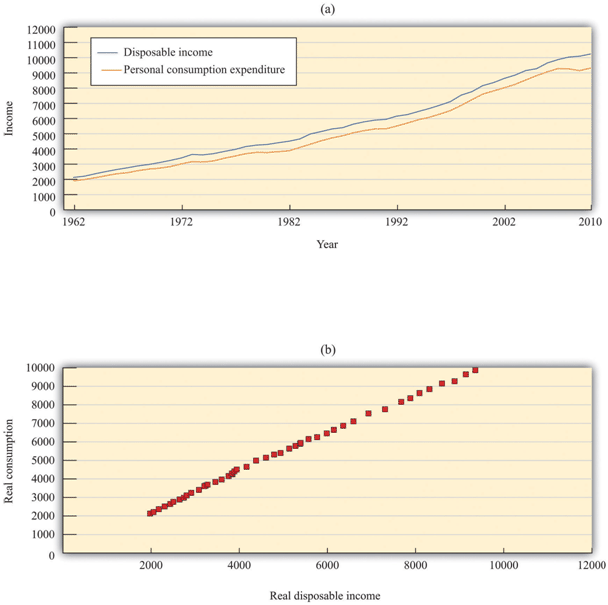
Source: Economic Report of the President (Washington, DC: GPO, 2011), table B-31, accessed September 20, 2011, www.gpoaccess.gov/eop/tables11.html.
The charts show consumption and personal disposable income (in billions of year 2005 dollars) from 1962 to 2010. Consumption and disposable income grew substantially over this time (a) and there is a close relationship between consumption and income (b).
The first thing we see in Figure 4 is that both consumption and disposable income grew substantially over the 1962–2010 period. This should come as no surprise. We know that the US economy grew over this period, so we would expect that disposable income and consumption would also grow. Figure 4 reveals that, as a consequence, there is a close relationship between consumption and income, and consumption expenditures are, on average, about 91 percent of disposable income. Although Figure 4 looks something like a consumption function, we should not take this relationship as strong evidence for our theory because it is primarily caused by the fact that both variables grew over time.
Consumption Response to the Kennedy Tax Cut
Now we return to the Kennedy tax cut. How well does our model perform in predicting the effects of the tax changes on consumption? Superficially, this seems like an easy question. We can examine the changes in consumption and income that arose after the tax changes and see whether these changes are consistent with the model.
There is a critical difference between our theory and reality, however. When we discussed the effects of a tax cut using our theory, we implicitly held everything else constant. We presumed that there was a change in taxes and no change in any other variable. For example, we assumed that government spending, investment spending, and net exports all did not change. In fact, other economic variables were changing at the same time that the new tax policy went into effect; these changes could also have affected consumption and disposable income. Looking at particular tax experiments is a messy business.
Taxes were cut in February 1964, and (real) disposable income increased by $430 billion, a much larger increase than in previous time periods. Consumption expenditures increased considerably during this period. Table 2 summarizes the behavior of GDP, disposable income, consumption, and the average propensity to consume over the 1960–68 period. Remember that these are real variables, measured in year 2000 dollars. The average propensity to consume is calculated as consumption divided by disposable income, and the marginal propensity to consume is calculated as the change in consumption divided by the change in disposable income.
| Year | Real GDP ($) | Disposable Income ($) | Consumption ($) | APC | MPC |
| 1960 | 2,501.8 | 1,759.7 | 1,597.4 | 0.91 | — |
| 1961 | 2,560.0 | 1,819.2 | 1,630.3 | 0.90 | 0.55 |
| 1962 | 2,715.2 | 1,908.2 | 1,711.1 | 0.90 | 0.91 |
| 1963 | 2,834.0 | 1,979.1 | 1,781.6 | 0.90 | 0.99 |
| 1964 | 2,998.6 | 2,122.8 | 1,888.4 | 0.89 | 0.74 |
| 1965 | 3,191.1 | 2,253.3 | 2,007.7 | 0.89 | 0.97 |
| 1966 | 3,399.1 | 2,371.9 | 2,121.8 | 0.89 | 0.96 |
| 1967 | 3,484.6 | 2,475.9 | 2,185.0 | 0.88 | 0.61 |
| 1968 | 3,652.7 | 2,588.0 | 2,310.5 | 0.89 | 1.11 |
Source: Economic Report of the President (Washington, DC: GPO 2004), accessed September 20, 2011, www.gpoaccess.gov/eop.
APC, average propensity to consume; MPC, marginal propensity to consume.
Disposable income increased as did consumption, in accordance with the predictions of our theory. As the theory predicts, the average propensity to consume decreased for most of this period. Likewise, in line with the theory, the marginal propensity to consume was less than 1 (in all years except 1968). Thus the evidence from this period is broadly consistent with the predictions that we made on the basis of our model.
Aggregate Income, Aggregate Consumption, and Aggregate Saving
The 1964 tax cut was not designed to influence consumption in isolation but rather to have an impact on the overall economy via its effect on consumption. So far, we have argued that a change in taxes leads to a change in disposable income and hence a change in consumption. Now we complete the story, noting that a change in consumption will itself affect the level of real GDP and hence have further effects on the level of disposable income.
In the case of the Kennedy tax cut of 1964, the economists advising the administration at that time had a fairly specific idea of how changes in consumption would affect the overall economy. They argued that the $10 billion tax cut would lead to an increase in GDP of about $20 billion each year. How did they create this estimate? To answer this question, we need to embed our theory of consumption in the aggregate expenditure model.
We motivated our consumption function by thinking about the behavior of an individual household. We now presume that our household is in some sense average, or representative of the entire economy, so the consumption relationship holds at an economy-wide level. Different households might actually have different consumption functions, but when we add them together, we still expect to find an aggregate relationship similar to the one we have described. The economists of the time used a framework that was closely based on the aggregate expenditure model. When prices are sticky, the level of GDP is determined in that model by the condition that planned spending and actual spending are equal. The model tells us that the level of real GDP depends on the level of autonomous spending and the multiplier,
real GDP = multiplier × autonomous spending,
where the multiplier is calculated as (11−marginal propensity to spend). Given the level of autonomous spending in the economy and given a value for the marginal propensity to spend, we can calculate the equilibrium level of real GDP.
The marginal propensity to spend is not the same thing as the marginal propensity to consume, although they are connected. The marginal propensity to spend tells us how much total spending changes when GDP changes. Total spending includes not only consumption but also investment, government purchases, and net exports, so if any of these are responsive to changes in GDP, then the marginal propensity to spend is affected. Likewise, autonomous spending is not the same as autonomous consumption. Autonomous spending is the sum of autonomous consumption, autonomous investment, autonomous government purchases, and autonomous net exports. Finally, the marginal propensity to consume measures how consumption responds to changes in disposable income, not GDP.
In our analysis here, we continue to focus on consumption and suppose that the other components of spending—government spending, investment, and net exports—are exogenous. That is, these variables are all unaffected by changes in income and so are all included in autonomous spending. In addition, we presume that the amount that the government spends is not affected by the amount that it receives in tax revenue.
To find out the effects on the economy of a change in income taxes, we take the equation for real GDP and write it in terms of changes:
change in real GDP = multiplier × change in autonomous spending.
This equation tells us we need two pieces of information to work out the effect of a tax change:
- The marginal propensity to spend because this allows us to calculate the multiplier
- The effect of a tax change on autonomous spending
Let us think about the marginal propensity to spend first. We want to know the answer to the following question: if GDP changes by some amount (say, $100), what will happen to spending? There are three pieces to the answer.
- A change in GDP leads to a change in personal income. Remember from the circular flow of income that GDP measures production, income, and expenditure in the economy. Firms receive income when they sell their products. Most of that income finds its way into the hands of households in the form of wage and salary payments or dividend payments. Firms hold onto some of the income that they generate to replace worn-out capital goods and finance new investments. In the early 1960s, personal income was about 78 percent of GDP. So if GDP increased by $100, we would expect personal income to increase by about $78.
- A change in personal income leads, in turn, to a change in disposable income. As we explained at length, personal income is taxed, so disposable income is less than personal income. Since we are considering the effects of a change in taxes, we need an estimate of the marginal tax rate facing consumers. We know from Figure 27.3 that this varied across individuals, but researchers have estimated that for the economy as a whole, the marginal tax rate in 1964 was about 22 percent. Robert J. Barro and Chaipat Sasakahu provide estimates of the “average marginal tax rate.” Barro and Sasakahu, “Measuring the Average Marginal Tax Rate from the Individual Income Tax” (NBER Working Paper No. 1060 [Reprint No. r0487], June 1984), http://www.nber.org/papers/w1060. To put it another way, households would keep about 78 percent (= 100 percent – 22 percent) of their personal income. So if personal income increased by $78, disposable income would increase by about $61 (= 0.78 × $78). (It is a meaningless coincidence that these two numbers are both 78 percent.)
- Finally, a change in disposable income leads to a change in consumption. According to the 1964 Economic Report of the President, the CEA thought that the marginal propensity to consume was about 0.93. So if disposable income increased by $61, we would expect consumption to increase by about $57 (= 0.93 × $61).
Putting these three together, therefore, we see that an increase in GDP of $100 causes consumption to increase by $57. The marginal propensity to spend in this economy was equal to about 57 percent.
Now let us think about the change in autonomous spending. We have said that taxes were cut by about $10 billion. We expect that most of this tax cut ended up in the hands of consumers. Based on the marginal propensity to consume of 0.93, we would, therefore, expect there to be an increase of about $9.3 billion in autonomous consumption,
change in autonomous spending = $9.3 billion.
Putting these two results together, we find that our prediction for the change in GDP as a result of the tax cut is
change in real GDP = multiplier × change in autonomous spending = 2.3 × $9.3 billion = $21.4 billion.
Our answer is not exactly equal to the $20 billion predicted by the CEA, but it is very close. As you might expect, the CEA was working with a more complicated model than the one we have explained here, and, as a result, they came up with a slightly smaller number for the multiplier.
A Word of Warning
All our analysis so far has ignored the fact that, through the price adjustment equation, increased real GDP causes the price level to rise. This increase in prices serves to choke off some of the effects of the increase in spending. In effect, we have ignored the supply side of the economy. It is not that the Kennedy-Johnson administration economists were naïve about the supply side, but they thought the demand side movements were much more relevant for short-run policymaking purposes. More recent economic experience has convinced economists that we ignore the supply side of the economy at our peril. Modern macroeconomists would be careful to augment this story with a discussion of price adjustment.
Tax Cuts and Private Saving
We have already conducted most of the analysis we need to examine the effects of tax cuts on saving. We know that a tax cut increases disposable income. Our theory of consumption smoothing tells us that households will respond by increasing consumption and savings. Specifically, we predict that a dollar’s worth of tax cuts will cause saving to increase by (1 − marginal propensity to consume). It is tempting to conclude that tax cuts, therefore, will lead both to higher consumption, increasing output now, and to higher saving, increasing output in the future. Such an argument is not right because it looks only at saving by households. We also need to look at the effect of the tax cut on the government surplus or deficit.
Tax Cuts and National Saving
If the government is spending more than it receives in tax revenues, then it is running a deficit. Conversely, if it is spending less than it receives in tax revenues, it is running a surplus. National savings is the combined savings of the government and the private sector.
If the government is running a deficit, national savings = private savings − government deficit,
If the government is running a surplus, national savings = private savings + government surplus.
These are just two different ways of saying the same thing because, by definition, the government surplus equals minus the government deficit.
What happens if the government cuts taxes? If there are no associated changes in government spending, then tax cuts translate dollar for dollar into the government budget. One million dollars worth of tax cuts will increase the deficit (or decrease the surplus) by exactly $1 million. So even though a tax cut of a dollar increases private savings by $(1 − marginal propensity to consume), it costs the government $1. The net effect (to begin with) is to reduce national savings by an amount equal to the marginal propensity to consume.
If the tax cut succeeds in increasing income, there is additional savings resulting from the multiplier process. Still, we expect the overall effect is a decrease in national savings. For example, consider the Kennedy tax cut again. Taxes were cut by $10 billion. The resulting change in income was roughly $20 billion. With the marginal propensity to save equal to 0.07, the offsetting increase in private savings would have been about $1.4 billion. Evidently, the result was a large decrease in national savings.
Here we see one of the biggest problems with tax cuts. They are attractive in the short run because they stimulate aggregate demand and increase output. They are also attractive politically, for obvious reasons. Unfortunately, they have the adverse long-run consequence of reducing national savings. When national savings decreases, the economy does not build up its capital stock so quickly, so future living standards are lower than they would otherwise be.
The Reagan Tax Cut
When Ronald Reagan was elected US president in 1980, the US economy was not in very good shape. The 1970s had been a very difficult time for economies throughout the world. The oil-producing nations of the world, acting as a cartel, had increased oil prices substantially, and, as a result, energy costs had increased. These energy prices triggered a severe recession in the mid 1970s and a smaller recession in the late 1970s. Figure 5: shows the US real gross domestic product (GDP) for this period. As well as recessions, the United States was suffering from inflation that was very high by historical standards: prices were increasing by more than 10 percent a year.
Figure 5: Real GDP in the 1970s
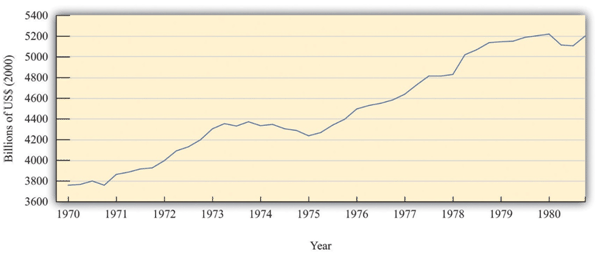
Source: Bureau of Economic Analysis. The figure shows real GDP in the 1970s. There was a protracted recession in the mid-1970s and a smaller recession toward the end of the decade.
President Reagan and his economic advisors argued that high taxes were one of the causes of the relatively poor performance of the US economy. In particular, they claimed that taxes on income were deterring people from working as hard as they would otherwise. Unlike President Kennedy’s advisors, who had argued that income tax cuts would increase real GDP by stimulating aggregate expenditure, Reagan’s advisors said that tax cuts would increase potential output. Proponents of this economic view became known as supply siders because their focus was on the production of goods and services rather than the amount of spending on goods and services.
After his inauguration, President Reagan pushed hard for changes in the tax code, and Congress enacted the Economic Recovery Tax Act (ERTA) in 1981. This law reduced tax rates substantially.
The main mechanism that the supply-siders proposed was that lower income taxes would increase the incentive to work. To analyze this claim, we need to investigate how the decision to supply labor depends on income taxes. As with our analysis of consumption, we look at labor supply by thinking about the behavior of a single household. We then suppose that the household can be taken as representative of the entire economy.
Labor Supply
Each individual faces a time constraint: there are only 24 hours in the day, which must be divided between working hours and leisure hours. An individual’s time budget constraint says that, on a daily basis, leisure hours + working hours = 24 hours.
The labor supply decision is equivalently the decision about how much leisure time to enjoy. This decision is based on the trade-off between enjoying leisure and working to purchase consumption goods. People like having leisure time, and they prefer more leisure to less. Leisure can be thought of as a “good,” just like chocolate or blue jeans or cans of Coca-Cola. People sacrifice leisure, working instead because the money they earn allows them to purchase goods and services.
To see this, we first rewrite the time budget constraint in money terms. The value of an hour of time is given by the nominal wage. Multiplying through the time budget constraint by the nominal wage gives us a budget constraint in dollars rather than hours:
(leisure hours × nominal wage) + nominal wage income = 24 × nominal wage.
The second term on the left-hand side is “nominal wage income” since that is equal to the number of hours worked times the hourly wage.
Because wage income is used to buy consumption goods, we replace it by total nominal spending on consumption, which equals the price level times the number of consumption goods purchased:
(leisure hours × nominal wage) + (price level × consumption) = 24 × nominal wage.
This is the budget constraint faced by an individual choosing between consuming leisure and consumption. Think of it as follows: it is as if the individual first sells all her labor at the going wage, yielding the income on the right-hand side. With this income, she then “buys” leisure and consumption goods. The price of an hour of leisure is just the wage rate, and the price of a unit of consumption goods is the price level. Finally, if we divide this equation through by the price level, we see that it is the real wage (the wage divided by the price level) that appears in the budget constraint:
(leisure hours × real wage) + consumption = 24 × real wage.
It is the real wage, not the nominal wage, that matters for the labor supply decision.
Changes in the Real Wage
What happens if there is an increase in the real wage? There are two effects:
- There is a substitution effect. An increase in the real wage means that leisure has become relatively more expensive. You have to give up more consumption goods to get an hour of leisure time. If leisure becomes more expensive, we would expect the household to “buy” fewer hours of leisure and more consumption goods—that is, to substitute from leisure to consumption. This effect predicts that the quantity of labor supplied will increase.
- There is an income effect. An increase in the real wage makes the individual richer—remember that we can think of income as equaling 24 × the real wage. In response to higher income, we expect to see the household increase its consumption of goods and services and also increase its consumption of leisure. This effect predicts that the quantity of labor supplied will decrease.
Putting these predictions together, we must conclude that we do not know what will happen to the quantity of labor supplied when the real wage increases. On the one hand, higher real wages make it attractive to work more since you can get more goods and services for each hour of time that you give up (the substitution effect). On the other hand, you can get the same amount of consumption goods with less effort, which makes it attractive to work less (the income effect). If the substitution effect is stronger, the labor supply curve has the standard shape: it slopes upward, as in Figure 6:.
Figure 6: Labor Supply
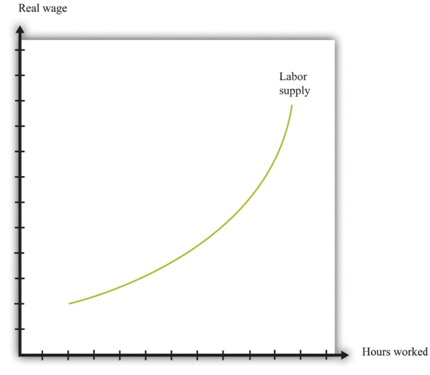
The response of the quantity of labor supplied to the real wage depends on both an income effect and a substitution effect. When the substitution effect is larger than the income effect, the supply curve has the “normal” upward-sloping shape.
In the end, the shape of the labor supply curve is an empirical question; we can answer it only by going to the data. And as you might be able to guess, it turns out to be a difficult question to answer, once we start dealing with the complexities of different kinds of labor. The view of most economists who have studied labor supply is that higher real wages do lead to a greater quantity of labor supplied, but the effect is not very strong. The income effect almost cancels out the substitution effect. This means that the labor supply curve slopes upward but is quite steep.
The Effect of the Reagan Tax Cuts on the Supply of Labor
Suppose an individual knows the nominal wage but also knows that she is going to be taxed on any income that she earns at the going income tax rate. The wage rate that matters for her decision is the after-tax real wage. Her real disposable income is:
disposable income = hours worked×(1−tax rate)×(nominal wage/price level)
= hours worked×(1−tax rate)×real wage.
All our discussion of labor supply continues to hold in this case, except that we need to replace the real wage with the after-tax real wage since it is the after-tax wage that matters to the individual.
Figure 7: shows the effect of a cut in taxes. If the labor supply curve slopes upward, the tax cut leads to an increase in the quantity of labor supplied. And if labor supply increases, then potential output also increases. In other words, one effect of tax cuts is to induce people to work harder and produce more real GDP. To keep things simple, Figure 8 is drawn supposing that there is no change in the equilibrium real wage as a result of the tax cut. In fact, we would expect the real wage to decrease somewhat as well. Buyers of labor as well as sellers of labor would benefit from the tax cut. Indeed, it is this decrease in the real wage that induces firms to purchase the extra labor that individuals wish to supply. (If we included this in our picture, then the after-tax real wage would still increase but by less than shown in the figure.)
Figure 7: Labor Supply Response to Tax Cut
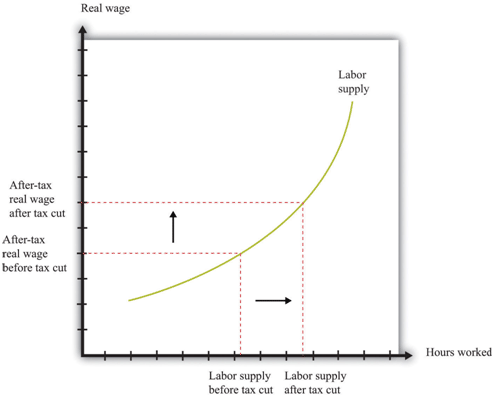
The wage that matters for labor supply decisions is the after-tax real wage. If income taxes are cut, and the real wage is unchanged, then households will supply more labor.
To view a Congressional Report on Tax Rates since 1945 visit Taxes and the Economy.
The Laffer Curve
Supply-side economics was controversial and generated a great deal of debate back in the 1980s and since. Yet the argument that we have just presented is not really controversial at all. Almost all economists agreed that as a matter of theory, cuts in taxes could lead to increases in the quantity of labor supplied. The disagreements concerned the magnitude of the effect.
Some proponents of supply-side economics made a much stronger claim. They said that the positive effects on labor supply could be so large that total tax revenues would increase, not decrease. They argued that even though the government would get less tax revenue on each dollar earned, people would work so much harder and generate so much more taxable income that the government would end up with more revenue than before.
This argument was encapsulated in the so-called Laffer curve. Economist Arthur Laffer asked what would happen if you graphed tax revenues as a function of the tax rate. Obviously (he observed) if the tax rate is zero, then tax revenues must be zero. And, Laffer argued, if the tax rate were 100 percent, so the government took every penny you earned, then no one would have an incentive to work at all, and the quantity of labor supplied would drop down to zero. Once again, income tax revenues would be zero. In between, tax revenues are positive. Figure 8: shows an example of a Laffer curve. There is some tax rate that will lead to the maximum possible revenue for the government. This itself is not that interesting: the goal of the government is not to raise as much tax revenue as possible. But if the tax rate lies to the right of that point, then—as the picture shows—a cut in taxes will increase tax revenues.
Figure 8: Laffer Curve
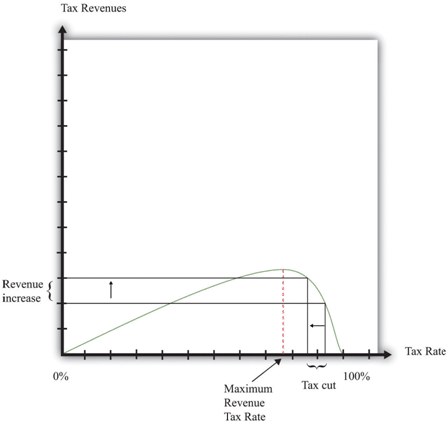
The Laffer curve says that it is possible for a reduction in the tax rate to lead to an increase in tax revenues. Although this is a theoretical possibility at very high tax rates, most economists view the Laffer curve as a theoretical curiosity with limited applicability to real economies.
Just as almost all economists agreed that there would be some supply-side effects of income tax cuts, almost all economists agreed that the Laffer curve argument was inapplicable to the US economy (or indeed any other economy). The evidence indicated that the effects of tax cuts on hours worked were likely to be relatively small. Almost no economists actually believed that the economy was on the wrong side of the Laffer curve, where tax cuts could pay for themselves.
Unfortunately, the Laffer curve argument was politically appealing, even though it was not supported by economic evidence. Buoyed by this argument, President Reagan oversaw both tax cuts and big increases in government spending. As a result, the US government ran large budget deficits. Following on from the ERTA, President Reagan and President George H. W. Bush after him were both forced to increase taxes to bring the budget back under control. The economic history of the United States in the 1980s was quite complex. Because this chapter concerns income taxes, we have considered only one of the policy changes of the Reagan administration. Other changes in tax policy were designed to promote savings. We have not discussed other aspects of President Reagan’s fiscal policy (there were large increases in government purchases), the tight monetary policy pursued by the Federal Reserve or the behavior of interest rates and exchange rates. All these are matters for other chapters.
In Conclusion
Our goal in this chapter was to understand the effects of tax changes on aggregate consumption and aggregate output. A tax cut puts more income in the hands of households, and thus consumption increases. The increase in consumption, in turn, leads to an expansion in the overall level of economic activity. The framework does a good job of describing and explaining actual economic outcomes during the Kennedy tax cut. We can thus have some faith that our basic framework is reasonably sound. Having said that, it is a very simple model that does have some deficiencies, most notably its neglect of the supply side of the economy.
Income tax cuts also decrease overall national saving. Income tax cuts increase household disposable income and lead to increased saving by households (as well as increased consumption). At the same time, however, income tax cuts mean that the government is saving less (or borrowing more). The net effect is to decrease national saving. The theory of economic growth tells us that reduced saving has the effect of decreasing future standards of living.
We then examined the Reagan tax cuts of the 1980s. These tax cuts were aimed at stimulating employment and output by encouraging people to work more. The belief that tax cuts lead to an increase in the quantity of labor supplied is consistent with basic microeconomic principles, but there is disagreement about the likely size of the effect.
Although we cast our discussion of the effects of taxes on spending using the tax cuts of the Kennedy and Reagan administrations, the lesson is more general. It is common for the United States and other countries to use variations in income tax rates as a tool of intervention. We highlighted several effects of such interventions. Income tax changes alter the level of household disposable income and thus influence consumption expenditures; they affect saving and capital accumulation, and they affect labor supply. This policy tool, therefore, gives the government considerable influence on the aggregate economy.
Indeed, when the crisis of 2008 hit the world’s economies, many countries responded by implementing expansionary fiscal policies, including cuts in taxes. Australia, the United Kingdom, Singapore, Austria, and Brazil are just a few of the countries who cut taxes in response to the crisis.
We used the Kennedy tax cut to illustrate demand-side effects and the Reagan tax cut to illustrate supply-side effects because those were the channels emphasized by the economic advisors at the time. Just about every change in the income tax code, however, has effects on consumption, saving, and labor supply. Every change in the code has short-run effects and long-run effects, and, as we have seen, these effects can be contradictory. Thus whenever you hear or read about proposed changes in taxes, you should try to remember that all these different stories will be in operation. The politicians and pundits who are supporting or opposing the change will typically talk about only one of them, depending on the spin they wish to convey. The analysis of this chapter should help you always see the bigger picture.
Finally, remember that tax changes will typically have major effects on the distribution of income. There are winners and losers from every change in the tax code. This, above all, is why changes in the tax code are an endless source of political debate.
To view current issues visit the Council of Economic Advisors.
Key Takeaways on Kennedy
- Beginning in the early 1960s, the growth of real GDP began to slow. This provided the basis for the tax cut of 1964.
- The CEA economists used the aggregate expenditure model as the basis for their analysis of the effects of the tax cut.
- In response to the tax cut, consumption and real GDP both increased. This fits with the prediction of the aggregate expenditure model.
- Since the marginal propensity to consume is less than 1, a tax cut will lead to a household to consume more and save more.
- National savings, the sum of public and private savings, will generally decrease when there is a tax cut.
Key Takeaways on Reagan
- Prior to the Reagan tax cut, the US economy was experiencing both low growth in real GDP and high inflation.
- Reagan’s economic advisors stressed the effects of taxes on the supply side of the economy, and in particular the incentive effects of taxes on labor supply and investment.
- The Reagan tax cuts led to considerably higher deficits in the United States.
 Answer the self check questions below to monitor your understanding of the concepts in this section.
Answer the self check questions below to monitor your understanding of the concepts in this section.Self Check Questions
- What matters for labor supply decisions - the marginal tax rate or the average tax rate?
- According to the Laffer curve, does a tax cut always increase tax revenues?
- What was the state of the economy at the time of the Reagan tax cut?
- What framework was used for analyzing the effects of the Reagan tax cut?
- What were the effects of the Reagan tax cut?
- Go to the Bureau of Economic Analysis website. Visit the section on Personal Income. Examine what has happened recently to personal income and disposable income. Have they been increasing or decreasing? How does this affect you?
- Pick a country other than the United States. Can you find income tax rates for that country? How do they compare to the United States?
- Go to the IRS webpage. Suppose that you are a member of a married household with a total income of $55,000. What are your marginal and average tax rates? Compare those to the tax rates on individuals. Which group faces the higher marginal income tax rate?
- In the summer of 2010, the George W. Bush tax cuts were about to expire. What would the change in the tax rates be if tax cuts had been allowed to expire?
- Go online and research the current tax situation under the Trump administration. What are the criticisms of the current tax situation?

