Skip to main content
K12 LibreTexts

4.6.2: Equations of Parallel Lines

  1. Last updated
  2. Save as PDF
  • Page ID
    4323

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Equations of Parallel Lines

    Suppose a coordinate plane is transposed over the map of a city, and Main Street has the equation y=2x+5. If Broad Street runs parallel to Main Street, and it passes through the point (3, 14), what would be the equation of Broad Street? How do you know?

    Equations of Parallel Lines

    Recall that parallel lines have the same slope.

    Each of the graphs below have the same slope, which is 2. According to the definition, all these lines are parallel.

    Figure 4.6.2.1

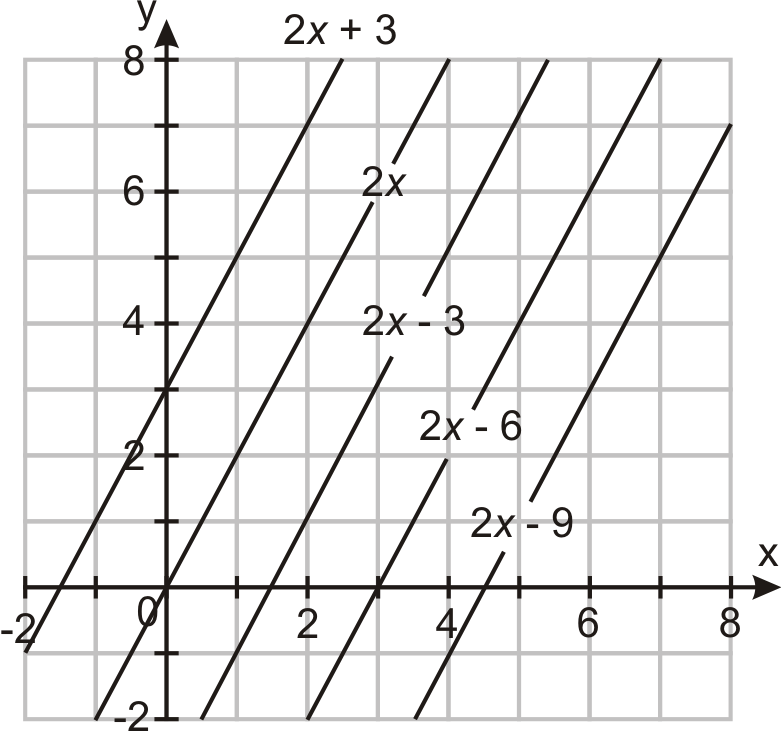
    Let's determine if y=1/3x−4 and −3x+9y=18 are parallel:

    The slope of the first line is 1/3.

    Any line parallel to this must also have a slope of 13.

    Find the slope of the second equation: A=−3 and B=9.

    slope=−A/B=3/9→1/3

    These two lines have the same slope so they are parallel.

    Writing Equations of Parallel Lines

    Sometimes, you will asked to write the equation of a line parallel to a given line that goes through a given point. In the following example, you will see how to do this.

    Let's find the equation of the following lines:

    1. The line parallel to the line y=6x−9 passing through (–1, 4).

    Parallel lines have the same slope, so the slope will be 6. You have a point and the slope, so you can use point-slope form.

    y−y1=m(x−x1)

    y−4=6(x+1)

    You could rewrite it in slope-intercept form:

    y=6x+6+4

    y=6x+10

    1. The line parallel to the line y−5=2(x+3) passing through (1, 1).

    First, we notice that this equation is in point-slope form, so let's use point-slope form to write this equation.

    y−y1=m(x−x1) Starting with point-slope form.

    y−1=2(x−1) Substituting in the slope and point.

    y−1=2x−2 Distributing on the right.

    y−1+1=2x−2+1 Rearranging into slope-intercept form.

    y=2x−1

    Examples

    Example 4.6.2.1

    Earlier, you were told that a coordinate plane is transposed over the map of a city, and Main Street has the equation y=2x+5. If Broad Street ran parallel to Main Street and it passes through the point (3, 14), what would be the equation of Broad Street?

    Solution

    Since Broad Street is parallel to Main Street, the line representing the two streets have the same slope. The slope of the equation for Main Street is 2 so the slope of the equation for Broad Street is also 2. Now, we can use the slope and the point (3, 14) to find the equation for Broad Street.

    y−y1=m(x−x1) Starting with point-slope form.

    y−14=2(x−3) Substituting in the slope and point.

    y−14=2x−6 Distributing on the right.

    y−14+14=2x−6+14 Rearranging into slope-intercept form.

    y=2x+8

    Example 4.6.2.2

    Find the equation of the line parallel to the line 4x−y=24 passing through (3, 2).

    Solution

    Since this is in standard form, we must first find the slope. For Ax+By=C, recall that the slope is m=−AB. Since A=4 and B=−1:

    m=−A/B=−4/−1=4

    Now that we have the slope, we can plug it in:

    y−y1=m(x−x1) Starting with point-slope form.

    y−2=4(x−3) Substituting in the slope and point.

    y−2=4x−12 Distributing on the right.

    y−2+2=4x−12+2 Rearranging into slope-intercept form.

    y=4x−10

    Review

    1. Define parallel lines.

    In 2-6, determine the slope of a line parallel to each line given.

    1. y=−5x+7
    2. 2x+8y=9
    3. x=8
    4. y=−4.75
    5. y−2=(1/5)(x+3)

    In 7-10, find the line parallel to it through the given point.

    1. y=−(3/5)x+2;(0,−2)
    2. 5x−2y=7;(2,−10)
    3. x=y;(2,3)
    4. x=−5;(−2,−3)

    Mixed Review

    1. Graph the equation 2x−y=10.
    2. On a model boat, the stack is 8 inches high. The actual stack is 6 feet tall. How tall is the mast on the model if the actual mast is 40 feet tall?
    3. The amount of money charged for a classified advertisement is directly proportional to the length of the advertisement. If a 50-word advertisement costs $11.50, what is the cost of a 70-word advertisement?
    4. Simplify √(112).
    5. Simplify √(122-72).
    6. Is √(3)−√(2) rational, irrational, or neither? Explain your answer.
    7. Solve for s: 15s=6(s+32).

    Review (Answers)

    To see the Review answers, open this PDF file and look for section 5.7.

    Additional Resources

    PLIX: Play, Learn, Interact, eXplore: Equations of Parallel Lines: Exploring Equations

    Video:

    Activity: Equations of Parallel Lines Discussion Questions

    Study Aid: Determining the Equation of a Line Study Guide

    Practice: Equations of Parallel Lines

    Real World Application: Parallel & Perpendicular Lines

    This page titled 4.6.2: Equations of Parallel Lines is shared under a CC BY-NC license and was authored, remixed, and/or curated by CK-12 Foundation via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.