1.4.2: Square and Cube Function Families
- Page ID
- 14136
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Square and Cube Function Families
Often, the most challenging part of completing a math problem is just getting started. Once you have a 'feel' for how a particular problem should be solved, crunching the numbers is generally not very difficult.
An understanding of function families can be a big help with this, as it gives you an idea of what a more complex function should look like once it has been graphed, just by identifying the parent or most simplified version of the function.
Do you know the parent functions for the Square, Cube, Square Root, and Reciprocal function families?
Square and Cube Function Families
Function Family: Square Functions
A square function is a 2nd degree equation, meaning it has an x2.
The graph of every square function is a parabola. A parabola has a vertex, and an axis of symmetry. The graph below shows these aspects of the graph of y = x2 - 3.
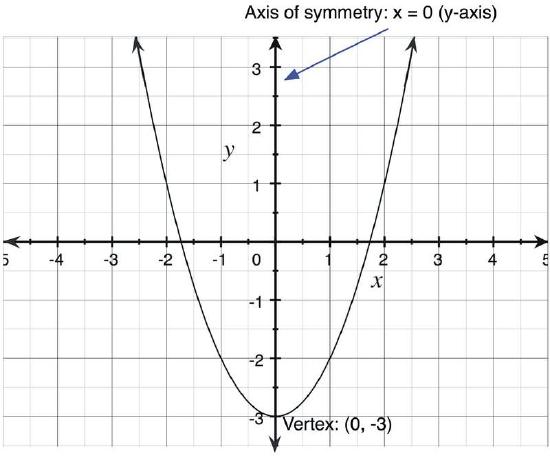
Function Family: Cubic Functions
A cube function is a third-degree equation: x3 and which does not contain negative or fractional exponents. In general, the graphs of cube functions have a particular shape, illustrated by the graph shown here:
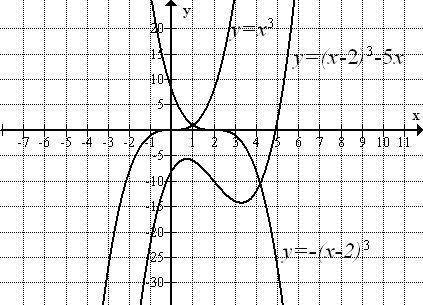
Cubic functions have a similar shape. However, only some cubic functions will have a relative maximum and minimum. For example, the graph of y = (x - 2)3 - 5x shown above, has a relative maximum around x = 0.7, and a relative minimum around x = 3.3. The shape of the cubic graph means that we can predict end behavior: one end will approach ∞, and the other will approach −∞.
It is important to note here that the cubic function grows faster than an associated quadratic function. For example, y = x3 grows faster than y = x2.
Function Family: Square Root Functions
Consider the parent of the family, \(\ y=\sqrt{x}\). The domain of the function is limited to real numbers ≥ 0, as the square root of a negative number is not a real number. Similarly, the range of the function is limited to real numbers ≥ 0. This may seem confusing if you think of squares having two roots. For example, 9 has two roots: 3, and -3. However, for \(\ y=\sqrt{x}\), we have to define the function value as the principal root, which means the positive root.
The function \(\ y=\sqrt{x}\) is shown below:
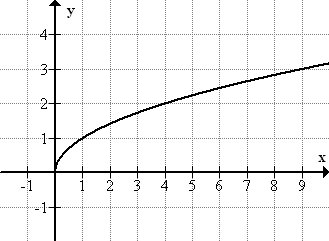
The same kind of limitations of domain and range will exist for any square root function.
Function Family: Reciprocal Functions
The function \(\ y=\frac{1}{x}\) has a rather surprising graph. First, the domain cannot include 0, as the fraction \(\ \frac{1}{0}\) is undefined. The range also does not include 0, as a fraction can only be zero if the numerator is zero, and the numerator of \(\ y=\frac{1}{x}\) is always 1.
In order to understand what these limitations mean for the graph, we will consider function values near x = 0 and y = 0. First, consider very small values of x. For example, consider x = 0.001. This yields \(\ y=\frac{1}{x}=\frac{1}{0.001}=1000\).
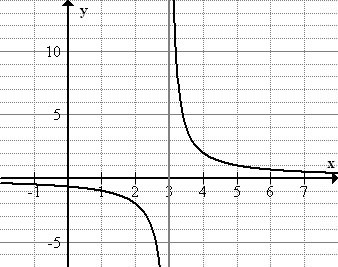
As we get closer and closer to x = 0, the function values approach ∞. On the other side of the x-axis the function values will approach −∞. We can see this behavior in the graph as a vertical asymptote: the graph is asymptotic to the y-axis.
We can also see in the graph that as x approaches +∞ or −∞, the function values approach 0. The exclusion of y = 0 from the range means that the function is asymptotic to the x-axis.
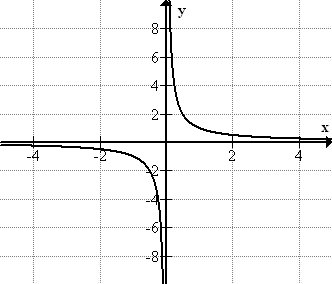 [Figure1]
[Figure1]Examples
Solution
Earlier, you were given a question about identifying the parent functions of various function families.
Can you identify the parent functions of the square, cube, square root, and reciprocal functions now?
Square: \(\ y=x^{2}\)
Cube: \(\ y=x^{3}\)
Square Root: \(\ y=\sqrt{x}\)
Reciprocal: \(\ y=1 / x\)
Learning the function families is one of the fastest way to graph complex equations. Using parent functions and transformations (which are detailed in another set of lessons), you can graph very complex equations rather easily.
Describe the end behavior of each function, and identify the parent function for each.
- \(\ y=x^{2}-1\)
- \(\ y=-x^{2}+1\)
Solution
- The parent of this function is \(\ y=x^{2}\).
The graph of this function is a parabola that opens up. Therefore \(\ \lim _{x \rightarrow \pm \infty}\left(x^{2}-1\right)=\infty\).
- The parent of this function is \(\ y=x^{2}\)
The graph of this function is a parabola that opens down. Therefore \(\ \lim _{-x \rightarrow \pm \infty}\left(x^{2}-1\right)=-\infty\).
All square functions have either a global maximum or minimum. The location of the maximum or minimum is always the vertex of the parabola. Square functions also share behavior in terms of their average rate of change. Consider for example the functions \(\ f(x)=x^{2}, g(x)=x^{2}-3\) and \(\ g(x)=2x^{2}-3\). The table below shows the average rate of change (ARC) of each function on several intervals.
Note: The ARC of a function on the interval (a, b) is \(\ \frac{f(b)-f(a)}{b-a}\).
Interval ARC of f(x) ARC of g(x) ARC of h(x) (-1, 0) (0, 1) 1 1 2 (1, 2) 3 3 6 (2, 3) 5 5 10 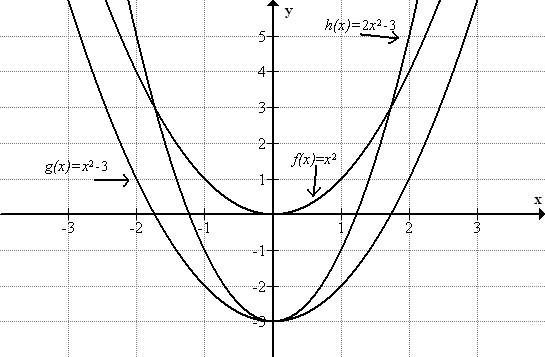
Notice that the average rate of change of f(x) and g(x) is the same on each interval, and the average rate of change of h(x) is twice that of the other two functions. You may also notice that the average rate of change follows a linear pattern: on each interval the rate increases at a constant rate of 2. While linear functions have a constant rate of change, quadratic functions have an average rate of change that follows a linear pattern.
Graph the function \(\ y=\sqrt{3-x}+1\), identify the parent function, and state the domain and range of the function.
Solution
The parent function is \(\ y=\sqrt{x}\)
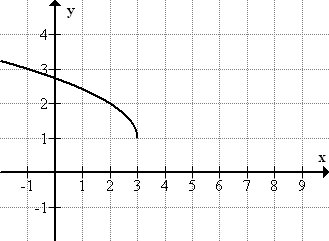
From the graph you can see that the function does not take on any x values above 3. (Why not?) Therefore the domain is limited to real numbers ≤ 3. The function’s lowest value is 1, so the range is limited to all real numbers ≥ 1 .
It is important to note that while the graph of a square root function might look as if it has horizontal asymptote, it does not. The function values will grow without bound (though relatively slowly!).
Graph the function \(\ f(x)=\frac{2}{x-3}\), identify the parent function, and identify horizontal and vertical asymptotes.
Solution
The parent function is \(\ y=1 / x\)
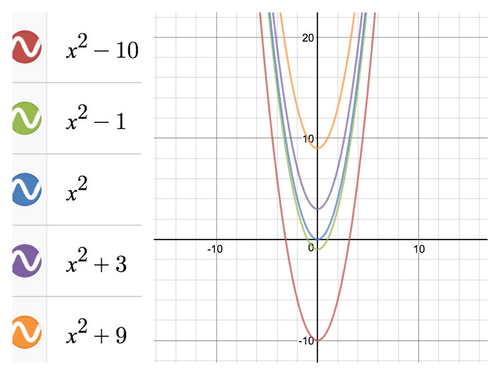
Identify the parent function within the following set of functions. Graph the set of functions using a graphing calculator. Identify similarities and differences of the set.
| f(x)=x2−10 | f(x)=x2−1 | f(x)=x2 |
|---|---|---|
| f(x)=x2+3 | f(x)=x2+9 |
Solution
 [Figure2]
[Figure2]- Parent Function: The parent function of this group of quadratic functions is the most basic function in the set: \(\ f(x)=x^{2}\)
- Similarities: width, shape, end behavior, and degree
- Differences: x and y intercepts
Identify the parent function within the following set of functions. Graph the set of functions using a graphing calculator. Identify similarities and differences of the set.
| f(x)=(x+9)3 | f(x)=(x+2)3 | f(x)=x3 |
|---|---|---|
| f(x)=(x−4)3 | f(x)=(x−8)3 |
Solution
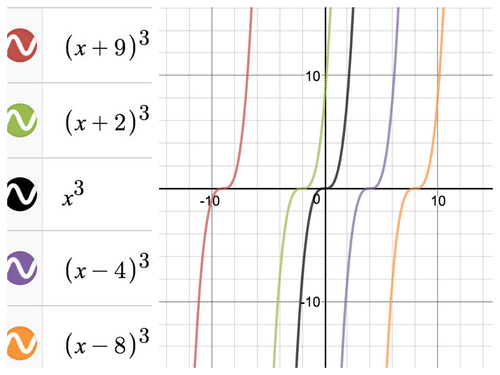 [Figure3]
[Figure3]- Parent Function: The parent function of this group of quartic functions is the most basic function in the set: \(\ y=x^{3}\)
- Similarities: end behavior, domain and range, direction, and width
- Differences: x and y intercepts, increasing and decreasing intervals
Review
- Explain what a square function is:
- What is a cube function?
- Describe the rate of growth of a cubic function related to the growth of a squared function
- For square root functions we have to define the function value as the positive root, also known as what?
- Why are reciprocal functions asymptotic to the x-axis?
Identify the parent function within each set of squared functions. Graph each set of functions using a graphing calculator. Identify similarities and differences of each set.
Set 1:
| f(x)=x2−10 | f(x)=x2−1 | f(x)=x2 |
|---|---|---|
| f(x)=x2+3 | f(x)=x2+9 |
- Set 1:
- Parent Function:
- Similarities:
- Differences:
Set 2:
f(x)=(x+10)2 f(x)=(x+4)2 f(x)=x2 f(x)=(x−2)2 f(x)=(x−5)2
- Set 2:
- Parent Function:
- Similarities:
- Differences:
Set 3:
f(x)=−x2 f(x)=x2
- Set 3:
- Parent Function:
- Similarities:
- Differences:
Use the above information and the vertex form of a quadratic equation: \(\ f(x)=a(x-h)^{2}+k\) to help you answer the following questions:
- How does the a value affect the graph?
- How does the h value affect the graph?
- How does the k value affect the graph?
- How are domain values similar/different?
- How are range values similar/different?
- Does the a, h, and/or k value affect the domain?
- Does the a, h, and/or k value affect the range?
Cubic Functions:
Circle the parent function within each set of cubic functions. Graph each set of functions using a graphing calculator. Identify similarities and differences of each set.
Set 4:
| f(x)=x3−5 | f(x)=x3−3 | f(x)=x3 |
|---|---|---|
| f(x)=x3+1 | f(x)=x3+6 |
- Set 4:
- Parent Function:
- Similarities:
- Differences:
Set 5:
f(x)=−x3 f(x)=x3 - Set 5:
- Parent Function:
- Similarities:
- Differences:
Vocabulary
| Term | Definition |
|---|---|
| ∞ | The symbol "∞" means "infinity", and is an abstract concept describing a value greater than any countable number. |
| axis of symmetry | The axis of symmetry of a parabola is a vertical line that passes through the vertex of the parabola. The parabola is symmetrical about this line. |
| Cube | The cube of a number is the number multiplied by itself three times. For example, "two-cubed" = 23=2×2×2=8. |
| Cubic Function | A cubic function is a function containing an x3 term as the highest power of x. |
| Function families | Function families are groups of functions with similarities that make them easier to graph when you are familiar with the parent function, the most basic example of the form. |
| Function Family | Function families are groups of functions with similarities that make them easier to graph when you are familiar with the parent function, the most basic example of the form. |
| Parabola | A parabola is the characteristic shape of a quadratic function graph, resembling a "U". |
| parent function | A parent function is the simplest form of a particular type of function. All other functions of this type are usually compared to the parent function. |
| principal root | The principal root is the positive root of a number. |
| Reciprocal Function | A reciprocal function is a function with the parent function \(\ y=\frac{1}{x}\). |
| square | The square of a number is the number multiplied by itself. |
| square function | A square function is a quadratic function. Its parent function is y=x2 and its graph is a parabola. |
| square root function | A square root function is a function with the parent function \(\ y=\sqrt{x}\). |
| Transformations | Transformations are used to change the graph of a parent function into the graph of a more complex function. |
| Vertex | The vertex of a parabola is the highest or lowest point on the graph of a parabola. The vertex is the maximum point of a parabola that opens downward and the minimum point of a parabola that opens upward. |
Image Attributions
- [Figure 1]
Credit: CK-12 Foundation
Source: Desmos Graphing Calculator - [Figure 2]
Credit: CK-12 Foundation
Source: Desmos Graphing Calculator - [Figure 3]
Credit: CK-12 Foundation
Source: Desmos Graphing Calculator

